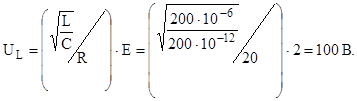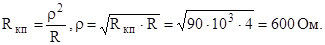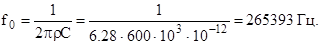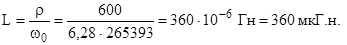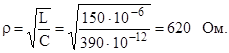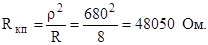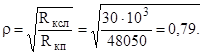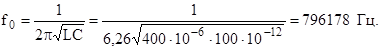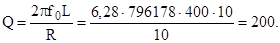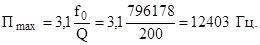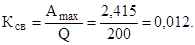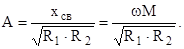Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Составитель доцент, канд.техн.наук Б.В. МатвеевСодержание книги
Поиск на нашем сайте
Воронеж 2005
Составитель доцент, канд.техн.наук Б.В. Матвеев
УДК 621.396
Методическое руководство к практическим занятиям № 1-4 по курсу "Электротехника" для студентов дневной и заочной форм обучения специальности 210201 "Проектирование и технология радиоэлектронных средств" / Воронеж, гос. техн. ун-т; Сост. Б В. Матвеев, Воронеж, 2005. 37 с.
В работе излагается материал, необходимый для получения практических навыков при решении задач по курсу "Общая электротехника и электроника". Каждое практическое задание содержит контрольные вопросы и задачи по теме, а также приводятся примеры решения типовых задний. Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 210200 «Проектирование и технология электронных средств» специальности 210201 «Проектирование и технология радиоэлектронных средств», дисциплине «Общая электротехника и электроника». Предназначено для студентов второго курса.
Табл. 1. Ил.27. Библиогр.: 2 назв. Рецензент канд. техн. наук В.П.Литвиненко
Ответственный за выпуск зав. кафедрой к.т.н. проф. Г.В.Макаров Печатается по решению редакционно-издательского совета Воронежского государственного технического университета
ã Воронежский государственный технический университет, 2005 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1 Тема занятия: «Линейные цепи при гармоническом Воздействии»
Литература: [ 1, С.36-47 ],[ 2, С.63-69; С.85-112], конспект лекций Домашнее задание Изучить по конспекту лекций и литературе материал по следующим пунктам: 1. Классификация электрический цепей. Линейные, нелинейные и параметрические цепи. Цепи с сосредоточенными и распределенными параметрами. 2. Идеализированные пассивные элементы: сопротивление, индуктивность и емкость. Компонентные уравнения для индуктивности и емкости: источники напряжения и тока. 3. Понятие о схемах электрических цепей: структурные, функциональные, принципиальные и эквивалентные (расчетные) схемы. 4. Основные определения, относящиеся к электрической схеме замещения (эквивалентной схеме): ветвь, узел, контур, граф. 5. Гармоническое колебание. Средневыпрямленное значение и среднеквадратическое значение гармонических функций. 6. Представление гармонических колебаний в виде проекций вращающихся векторов. Векторные диаграммы. 7. Гармонический ток в сопротивлении, индуктивности и емкости. Последовательное соединение R, L, C. Активное, реактивное и полное сопротивления. 8. Параллельное соединение R, L, C. Активная, реактивная и полная проводимости цепи. 9. Мощность в цепи переменного тока: средняя, реактивная, полная.
10. Согласование в цепи переменного тока. Коэффициент полезного действия.
Решить задачи: 1.1. Показать, что величина RC, L/R и 1.2. Используя векторное представление гармонического колебания, вычесть напряжение 5 sinωt из напряжения 10 cosωt. Ответ: 11,2 cos(ωt + 26030/).
1.3. На зажимах цепи, состоящей из последовательно соединенных сопротивления R = 50 Ом и индуктивности L = 0,1 Гн, задано напряжение u = Ответ: 59 Ом; 85 В; 53,4 В. i =
1.4. Через цепь, из параллельно соединенных сопротивления (R = 8,33 Ом) и индуктивности (L = 6,36 мГн), проходит ток 0,141 cosωt А; частота равна 500 Гц. Определить напряжение на параллельных ветвях. Ответ: u(t) = 1,1 cos(ωt + 22036/) В.
1.5. В цепи, состоящей из последовательно соединенных элементов R, C, L, определить действующее суммарное напряжение на всех элементах, если Ur = 2 В, Uc = 1 В, UL =1 В. Какая величина угла сдвига фазы между током и напряжени-ем? Нарисовать векторную диаграмму. 1.6. В цепи, состоящей из параллельно соединенных элементов R, C, L, определить действующее значение суммарного тока, если Ir = 1 A, IL = 3 A, I = 2 A. Какая величина угла сдвига фазы между током и напряжением? Нарисовать векторную диаграмму. 1.7. Используя условия задачи 1.3, определить среднюю мощность, отдаваемую источником напряжения в цепи.
Подготовиться к ответам на вопросы: 1. Какие электрические цепи называются линейными? 2. Какова связь между мгновенными значениями тока и напряжения на индуктивности? 3. Какова связь между мгновенными значениями тока и напряжения на емкости? 4. Как обозначаются на схемах идеальные и реальные источники напряжения и тока гармонической формы? 5. Сформулируйте определение электрической цепи. Что такое ветвь, узел и контур электрической цепи? 6. Как формулируются законы Кирхгофа? Приведите примеры для конкретных схем. 7. Какое колебание называется гармоническим, какими функциями времени оно выражается? 8. Назовите основные параметры гармонического колебания. В чем разница между мгновенными, амплитудными и действующими значениями напряжения и тока? 9. Для каких значений напряжения и тока справедлив закон Ома и справедливы законы Кирхгофа? 10. Как относятся между собой фазы тока и напряжения на сопротивлении, индуктивности и емкости? 11. Как определяется гармоническое колебание в виде вектора? 12. Изобразите графически в виде векторов два гармонических колебания, сдвинутых относительно друг друга на определенную фазу. Дайте интерпретацию в виде изображения на графике временных функций. 13. Напишите выражение для напряжения на индуктивности L uL (t) при iL = Im cos (ωt +φi). 14. Напишите выражение для тока через конденсатор C iC(t) при напряжении uC = Umcos (ωt +φi). 15. Что такое реальное сопротивление для индуктивности и емкости? Как зависит оно от частоты? 16. Чему равно полное сопротивление Z ветви из последовательно соединенных элементов R, L и C? 17. Изобразите векторную диаграмму для последовательно соединенных элементов R, L и C, приняв за исходный вектор общего тока. Определите в виде формулы суммарное действующее напряжение на R, L и C. 18. Дайте определение мгновенной, средней и реактивной мощности в цепи переменного тока. Как определяется полная мощность? 19. Сформулируйте условия согласования источника и нагрузки в цепи переменного тока. Как определяется коэффициент полезного действия?
Примеры решения задач
1.8. Показать, что величина R2С имеет размерность и индуктивности.
Решение
Воспользуемся формулой uL = L
Определим теперь размерность величины R2C и сопоставим ее с размерностью L. Используя формулу
1.9. К цепи, состоящей из последовательно соединенных сопротивления R = 50 Ом и катушки индуктивности L=50 мГн, подключен источник э.д.с. е = 100 сos103t В. Определить ток i(t). Решение Решение ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 2 Примеры решения задач 2.8. Определить i(t), если комплексная амплитуда тока задана в виде Im = -10-j5 A. Решение. Используя равенство –1 = e ±jπ, представим комплексные значения тока как Im = -(10 + j5) = e-jπ = e-jπ ·11,2·ej26,6˚ = 11,2ej (26,6˚ - 180˚) = 11,2e-j153,4˚. Для записи i(t) воспользуемся правилом перехода от комплексной формы записи гармонического колебания к временной, т.е. i(t) = Re{Im-ejωt}, таким образом, имеем, что i(t) = Re{11,2e-j153,4˚ ejωt} = Re{11,2ej(ωt-153,4˚)}= =Re{11,2·cos(ωt –153,4˚) + jsin(ωt –153,4˚)}=11,2(ωt –153,4˚) Ответ: i(t) = 11,2(ωt –153,4˚). 2.9. Сложить токи i1= 10sinωt и i2 = 10cos(ωt + π/4). Решение. Представляем выражения для токов в комплексной форме i1 = 10cos(ωt –90˚), I1m = 10e-j90˚, I1m = 10cos90˚ - j10sin90˚ = -j10˚, i2 = 10cos(ωt + π/4), I2m =10ej45˚, I2m = 10cos45˚ + j10sin45˚ =7,07 + j7,07. Произведем сложение токов Im = I1m +I2m = -j10 +7,07 +j7,07 = 7,07- j2,97 = =
Преобразуем комплексную запись тока в тригонометрическую
i(t) =Re{7,67e-j22,8˚ · ejωt} = Re{7,67ej(ωt -22,8˚ }= = Re{7,67cos(ωt –22,8˚)+ j7,67sin(ωt –22,8˚)}=7,67cos(ωt–22,8˚). Ответ: 7,67cos(ωt –22,8˚).
2.10. Вычислить комплексное значение тока в цепи источника напряжения в схеме
Рис. 2.2
с учетом, что e(t)=20cos314t B, R1=10 Oм, R2=100 Oм, С = 100 мкф. Решение
Представим e(t) в комплексной форме, что с учетом нулевой начальной фазы выразится как E= 20 В. Вычислим комплексное сопротивление
Z = R1 + = 10 + Определяем комплексное значение тока İ = = Ответ: İ = 0,57ej56,4
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 3
Решить задачи 3.1. Сопротивление R=2 Ом и емкость С = 0,191 мкФ соеденены параллельно. Найти эквивалентную схему с последовательным соединением R и C при частоте f = 1 Мгц. Ответ: R = 0,296 Ом; C = 0,224 мкФ.
Рис. 3.1 Используя эквивалентное преобразование источника напряжения в источник тока, напряжение Ответ:
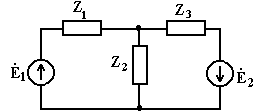
3.3. В схеме Ė1=120 В, Ė2=110 В, Z1 = Z2 = Z3=0,4+j0,6 Ом.
Рис. 3.2 Определить напряжение а) метод наложения, б) теорему об эквивалентном источнике напряжения, в) метод контурных токов.
Составить систему уравнений для определения токов в ветвях общим методом и методом узловых потенциалов.
Подготовиться к ответам на вопросы: 1. Сформулируйте условия, которые необходимо выполнить при замене одного участка цепи другим, эквивалентным первому. 2. Как перейти от последнего соединения элементов к эквивалентному параллельному соединению? 3. Как перейти от параллельного соединения элементов к эквивалентному последовательному соединению? 4. Объясните, почему эквивалентный переход от параллельного соединения к последовательному и наоборот верен только для одной и той же частоты f? 5. Объясните, что такое напряжение холостого хода 6. Сформулируйте теорему об эквивалентном источнике напряжения. 7. Какой принцип теории электрических линейных цепей используется при расчете методом наложения? 8. Сформулируйте порядок определения тока в ветви при расчете методом наложения. 9. Дайте определения понятиям: ветвь, узел, контур, граф. 10. Сформулируйте определение для первого и второго законов Кирхгофа. 11. Как определить число независимых узлов и контуров для расчета цепи по общему методу? 12. Поясните порядок составления уравнений по общему методу расчета электрической цепи. 13. Чем отличается метод контурных токов от общего метода? 14. Поясните порядок составления уравнений по методу контурных токов. 15. Какой закон Кирхгофа используется в методе узловых потенциалов?
Примеры решения задач
3.4. В схеме, имеющей C=10 мкФ, R=10 Ом, L= 100 мГн, вычислить комплексное сопротивление цепи для ω = 377 рад/с, используя правило эквивалентных преобразований.
Рис. 3.3
Решение
Цепь, состоящую из последовательно соединенных R и L, представим эквивалентной цепью из параллельно соединенных элементов и определим g и b этой цепи
Определим теперь общую проводимость цепи
Комплексное сопротивление цепи находим как
Ответ: Ż =13,5 + j43,4 Ом.
3.5. Сопротивление R=10 Ом и индуктивность L=10 мГн соединены параллельно. Найти эквивалентную схему с последовательным соединением R и L при частоте f= 1000 Гц.
Решение
Записываем выражение для комплексного сопротивления, т.е.
Таким образом, мы получим, что R=10 Ом и ωL =1,56 Ом.
Определяем, что В итоге получаем, что эквивалентная схема с последовательным соединением состоит из R=9,75 Ом и L=2,48·10-4 Гн= =0,248 мГн. Ответ: R=9,75 Ом, L=0,248 мГн. 3.6. В схеме изменить источники напряжения на эквивалентные источники тока, если Е1=10 В, Е2=30 В, Z1 = 20+j10 Ом, Z2 = 5+j4 Ом.
Рис. 3.4 Решение Произведем замену источников напряжения на эквивалентные источники тока, перечертив схему
Рис. 3.5 Значения величин токов İ1 и İ2 определим как İ1 = İ2 = Для обратного перехода от источника тока к эквивалентным источникам напряжения необходимо, перечертив схему, вычислить значения E по формуле Ė = İ·Z.
Рис. 3.6 Решение Определим напряжение холостого хода Uхх между точками 1 и 2, разорвав ветвь
Сопротивление короткого замыкания Zкз между точками 1 и 2, определим из схем (рис. 3.7, рис. 3.8.), т.е.
Ток через Z5 определим в соответствии с теоремой об эквивалентном источнике напряжения по формуле
Рис. 3.7 Рис. 3.8 3.8. Методом наложения определить напряжение на ветви Z3 в схеме
Рис. 3.9 Решение
 в Z3 от источника тока İ1 (рис. 3.10), преобразовав его в эквивалентный источник напряжения Ė1 (рис. 3.11). в Z3 от источника тока İ1 (рис. 3.10), преобразовав его в эквивалентный источник напряжения Ė1 (рис. 3.11).
Рис. 3.10 Рис. 3.11
Разрываем цепь источника İ1 и определим частичный ток  в Z3 от источника İ2 (рис. 3.12), преобразовав его в эквивалентный источник напряжения Ė2 (рис. 3.13), т.е. в Z3 от источника İ2 (рис. 3.12), преобразовав его в эквивалентный источник напряжения Ė2 (рис. 3.13), т.е.
Рис. 3.12 Рис. 3.13
Определим ток İ3 в Z3 с учетом направлений э.д.с. Ė1 и Ė2 как
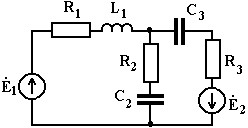
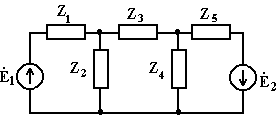
3.9. Используя метод контурных токов, определить токи в ветвях схемы (рис. 3.14).
Рис. 3.14 Ė1= 10 В, Ė2 = 20 В, L1 = 10 мГн, C1= C2 =100 мкФ, ω =10 рад/сек, R1= 50 Ом, R2= 5 Ом, R3=10 Ом. Решение Представим ветви в схеме (рис. 3.14) в виде комплексных сопротивлений Z1, Z2, Z3 (рис. 3.15).
Рис. 3.15 Определим значения комплексных сопротивлений Z1,.Z2, Z3:
Z1 = R1 + jωL1 = 50 + j103 ∙ 10 ∙ 10-3 = 60 + j10, Z2 = R2 + Z3 = R3 +
Составим систему уравнений по методу контурных токов, приняв за контурные токи: İ1 в контуре Ė1, Z1, Z2 и İ2 в контуре Е2, Z2, Z3 (рис. 3.16).
Рис. 3.16
İ2 (Z2 + Z3) – İ1 Z2 = Ė2.
Перепишем систему уравнений в виде
İ1(Z1 + Z2) - İ2 Z2 = Ė1 - I1 Z2 + I2 (Z2 + Z1) = Ė2.
Решим эту систему уравнений, используя метод Крамера, записав матрицу сопротивлений в виде
Подставляя значения сопротивлений Z1, Z2, Z3 в матрицу, получим
(-5 +j10) (15 - j20).
Найдем определитель матрицы ∆
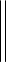 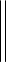 (65) (-5 + j10) (65) (-5 + j10)
∆ = = 1050 – j1200. (-5 +j10) (15 – j20)
Находим определители ∆ İ1 и ∆ İ2
Ė1 (-Z2 ) (10) (-5 + j10) ∆ İ1 = = =250-j400, Ė2 (Z2 + Z3) (20) (15 – j20)
(Z1 + Z2 ) Ė1 (65) (10) ∆ İ2 = = =1350-j100. (-Z2) Ė2 (-5 + j10) (20)
В соответствии с формулами Крамера находим контурные токи İ1 и İ2, т.е. İ1 = İ2 = Ток в ветви Z2 найдем как алгебраическую сумму токов İ1 и I2, т.е.
İZ3 = İ2 - İ1 = 1,258 + j0,144 – 0,292 + j0,047 =0,966 +j0,191 А.
Таким образом получаем, что
İZ1 = İ1 = 0,292 – j0,047 A, İZ2 = İ2 = 1,258 + j0,144 A, IZ2 = İ2 – I1 = 0,966 + j0,191 A.
3.10. Составить систему уравнений по методу узловых напряжений для схемы
Рис. 3.17
Для составления системы уравнений пор методу узловых напряжений используется только первый закон Кирхгофа. В схеме должны присутствовать только источники тока. Преобразуем схему с содержанием только источников тока, т.е.
Рис. 3.18 Величины токов определим из выражений
Зададимся также направлениями токов в ветвях, ориентируясь направлениями источников токов İ1 и İ2 (стрелки на схеме). Из трех узлов схемы узел 3 выберем за базовый (^) и относительно его зададимся узловыми напряжениями
-İ2 + После преобразования (раскроем скобки и приведем подобные члены) получим
Для решения системы уравнений можно использовать формулу Крамера, как в задаче 3.9, и далее, например, применить программу для вычисления определителей на основе прикладного пакета Mathcad. ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 4 Решить задачи 4.1. Для цепи, изображенной на рис. 4.1, напишите выражение для комплексного коэффициента передачи при следующих значениях элементов: R=100 Ом, С= 10 мкФ.
Рис. 4.1
4.2. Цепь состоит из катушки индуктивности L с сопротивлением потерь R и емкости C, соединенных последовательно. Напряжение на зажимах цепи равно 120 В. Определить напряжение на катушке индуктивности, если при этом напряжение на емкости равно 208 В.
Ответ: UL=240 В. 4.3. Какую индуктивность должен иметь последовательный контур, настроенный на частоту 106 Гц, чтобы он имел полосу пропускания П = 10 кГц, если сопротивление потерь R = 10 Ом? Ответ: L = 160 мкГн. 4.4. Рассчитать L и C параллельного контура, если резонансная частота f0=500 кГц, сопротивление потерь R=20 Ом, а резонансное сопротивление контура Rкп=20 кОм. Ответ: L=201 мкГн, C=500 пФ. 4.5. Сопротивление простого параллельного контура Rкп=10 Ом. Определить необходимый коэффициент включения p при подключении к контуру сопротивления нагрузки Rн=1000 Ом. Ответ: p = 0,1.
4.6. В связанных контурах два одинаковых контура, настроены каждый в отдельности на частоту f0=2∙106 Гц. Определить частоты связи f1 и f2, если известно, что активное сопротивление потерь каждого контура R=10 Ом, а сопротивление связи xсв=16 Ом. Емкость каждого контура равна 100 пФ. Ответ: f1=2015 кГц, f2=1984,3 кГц. Примеры решения задач 4.1. Для цепи, (рис.4.2.), определить постоянную времени τ, а также комплексный коэффициент передачи Рис. 4.2 Решение Для определения постоянной времени τ преобразуем цепь, используя эквивалентную замену источника напряжения на источник тока (рис. 4.3).
Рис. 4.3 и далее осуществим обратное преобразование (рис. 4.4).
Рис. 4.4
В результате определяем постоянную времени цепи τ как τ = R`∙C = Находим комплексный коэффициент передачи
Находим теперь выражение для АЧХ как
Для определения ФЧХ по формуле для φ (ω) = 0 – arctg ωτ = – arctg ωτ. Для построения графиков АЧХ и ФЧХ заполним таблицу значениями, вычисленными по формулам для │ Таблица 1.
По значениям из таблицы строим график (рис. 4.5).
Рис. 4.5
4.2. При некоторой частоте f в последовательном контуре xС = 220 Ом и xL= 170 Ом. Определить добротность контура, если известно, что сопротивление потерь контура R = 4 Ом.
Решение
Так как xC =
Добротность контура определиться как
Ответ: Q = 49,5.
4.3. Последовательный контур имеет: L = 200 мкГн, С = 200 пФ, R =20 Ом. Определить напряжение на катушке индуктивности при резонансе, если э.д.с. источника, питающего контур, Е = 2 В.
Решение.
Величина напряжения на катушке индуктивности определяется выражением UL = Q·E. Исходя из этого находим, что
Ответ: UL = 100 B. 4.4. При последовательном соединении L и C сопротивление контура в момент резонанса 4 Ом, при параллельном – 90 кОм. Емкость контура С=103 пФ. Определить волновое сопротивление контура ρ, индуктивность L и частоту генератора f. Решение Определяем волновое сопротивление контура по известным Rкп = 90 кОм и R = 4 Ом
Резонансную частоту контура определим из выражения для волнового сопротивления ρ =1/ω0С, с учетом, что ω0 =2πf0
Величину индуктивности находим, используя отношение ρ = ω0L, т.е.
Ответ: ρ = 600 Ом, f = 265393 Гц, L = 360 мкГн. 4.5. Общая индуктивность сложного параллельного контура L = 150 мкГн, а емкость С = 390 пФ, сопротивление потерь R= 8 Ом. Каким образом, индуктивность L должна быть распределена по ветвям контура, чтобы его входное сопротивление было равно Rксл = 30 кОм. Решение Определяем волновое сопротивление контура
Резонансное сопротивление простого параллельного контура будет равно
Величину коэффициента включения ρ находим из выражения
Часть индуктивности сложного контура определяется по известному ρ исходя из выражения L1 = ρ·L = 0,79·150·10-6 = 118,5·10-6 Гн = 118,5 мкГн. Оставшаяся часть индуктивности будет равна L2 = L – L1 = 150 – 118,5 = 31,5 мкГн. Ответ: L1 = 118,5 мкГн, L2 = 31,5 мкГн. 4.6. Система из двух одинаковых индуктивно связанных контуров имеет следующие параметры: L1 = L2 = 400 мкГн, C1= C2 = 100 пФ, R1 = R2 = 10 Ом. Определить наибольшую полосу пропускания и коэффициент связи, при котором обеспечивается эта полоса. Найти взаимную индуктивность М. Решение Определяем резонансную частоту одиночных контуров
Добротность контура будет равна
Наибольшая полоса пропускания будет равна
Коэффициент связи, соответствующий наибольшей полосе пропускания, будет равен
Взаимную индуктивность М определим из выражения для фактора связи
т.е.
Ответ: Пmax = 12403 Гц, Ксв = 0,012, М = 302 мкГн.
БИБЛИОГРАФИЧЕСКИЙ СПИСОК
1. Основы теории цепей: Учеб. для вузов – 3-е изд., испр.- М.: Высш. шк., 2000 – 575 с. 2. Основы теории цепей: Учеб. для вузов / Г.В. Зевеке, П.А.Ионкин, А.В.Нетушил, С.В.Страхов. 5-е изд., перераб.М.: Энергоатомиздат, 1989- 528 с.
Воронеж 2005
Составитель доцент, канд.техн.наук Б.В. Матвеев
УДК 621.396
Методическое руководство к практическим занятиям № 1-4 по курсу "Электротехника" для студентов дневной и заочной форм обучения специальности 210201 "Проектирование и технология радиоэлектронных средств" / Воронеж, гос. техн. ун-т; Сост. Б В. Матвеев, Воронеж, 2005. 37 с.
В работе излагается материал, необходимый для получения практических навыков при решении задач по курсу "Общая электротехника и электроника". Каждое практическое задание содержит контрольные вопросы и задачи по теме, а также приводятся примеры решения типовых задний. Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 210200 «Проектирование и технология электронных средств» специальности 210201 «Проектирование и технология радиоэлектронных средств», дисциплине «Общая электротехника и электроника». Предназначено для студентов второго курса.
Табл. 1. Ил.27. Библиогр.: 2 назв. Рецензент канд. техн. наук В.П.Литвиненко
Ответственный за выпуск зав. кафедрой к.т.н. проф. Г.В.Макаров Печатается по решению редакционно-издательского совета Воронежского государственного технического университета
ã Воронежский государственный технический университет, 2005 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ № 1
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 275; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.205.26 (0.015 с.) |

 имеют размерность времени а величина
имеют размерность времени а величина  - размерность сопротивления.
- размерность сопротивления. 100 cosωt. Частота f = 50 Гц. Вычислить полное сопротивление цепи и действующие значения напряжения на R и L; найти выражение для гармонического тока.
100 cosωt. Частота f = 50 Гц. Вычислить полное сопротивление цепи и действующие значения напряжения на R и L; найти выражение для гармонического тока. и определим размерность в основных единицах, т.е.
и определим размерность в основных единицах, т.е.
 и определяя размерность С, т.е. [с]= [i dt/duc]=
и определяя размерность С, т.е. [с]= [i dt/duc]=  , получим, что
, получим, что
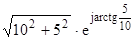 =
=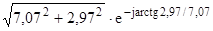 =7,67e-j22,8˚.
=7,67e-j22,8˚.
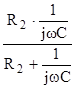 = 10 +
= 10 + 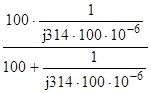 =
=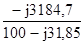 = 10 + 9,2 - j28,9 = 19б2 – j28,9.
= 10 + 9,2 - j28,9 = 19б2 – j28,9.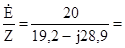 0,319 + j0,48 =
0,319 + j0,48 = e jarctg
e jarctg  = 0,57ej56,4
= 0,57ej56,4 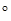 A.
A. 3.2. Два генератора, имеющих одинаковую частоту, соеденены параллельно по схеме
3.2. Два генератора, имеющих одинаковую частоту, соеденены параллельно по схеме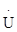 на параллельно соединенных генераторах.
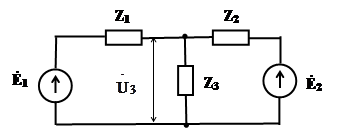
на параллельно соединенных генераторах. .
.
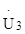 используя:
используя: и сопротивление короткого замыкания Zкз при определении тока в ветви по теореме об эквивалентном источнике напряжения?
и сопротивление короткого замыкания Zкз при определении тока в ветви по теореме об эквивалентном источнике напряжения?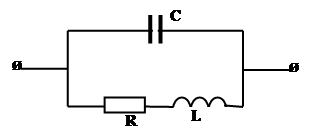

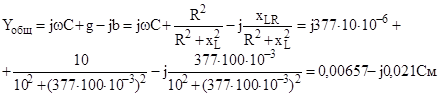
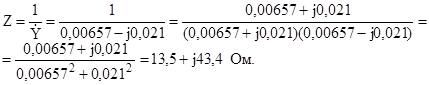
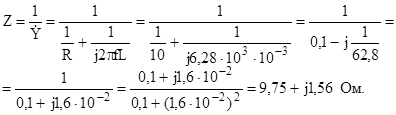


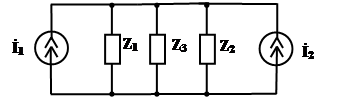
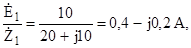 18
18
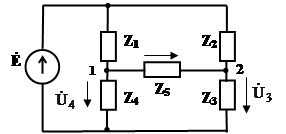 3.7. Используя теорему об эквивалентном источнике напряжения, определить ток I в сопротивлении Z5 для схемы (рис. 3.6.)
3.7. Используя теорему об эквивалентном источнике напряжения, определить ток I в сопротивлении Z5 для схемы (рис. 3.6.)
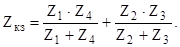


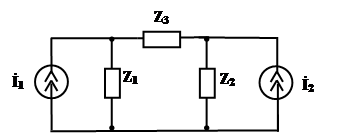
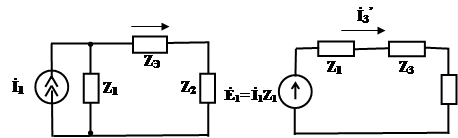
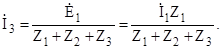



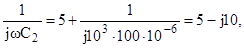


 İ1 (Z1 + Z2) - İ2 Z2 = Ė1
İ1 (Z1 + Z2) - İ2 Z2 = Ė1
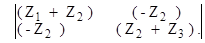

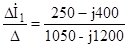 = 0,292 – j0,047 A,
= 0,292 – j0,047 A,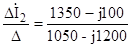 = 1,258 + j0,144 A.
= 1,258 + j0,144 A.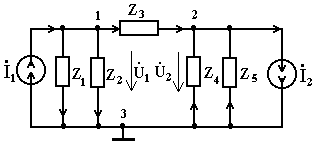

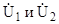 , стрелки которых показывают их направление от узлов 1 и 2 к узлу 3. Задача расчета цепи состоит в определении
, стрелки которых показывают их направление от узлов 1 и 2 к узлу 3. Задача расчета цепи состоит в определении  İ1 =
İ1 = 

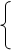
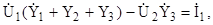
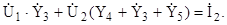

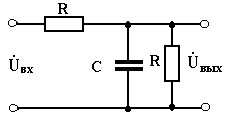
 Рассчитать и построить АЧХ и ФЧХ цепи, если R=10 Ом, С = 4 мкФ. Расчет АЧХ и ФЧХ сделать для следующих значений аргумента ωτ: 2; 1/3; 1/2; 1; 2; 3; 4; 5 и построить их на одном графике. По оси абцисс иметь два масштаба: а) для аргумента ωτ; б) для частоты ω.
Рассчитать и построить АЧХ и ФЧХ цепи, если R=10 Ом, С = 4 мкФ. Расчет АЧХ и ФЧХ сделать для следующих значений аргумента ωτ: 2; 1/3; 1/2; 1; 2; 3; 4; 5 и построить их на одном графике. По оси абцисс иметь два масштаба: а) для аргумента ωτ; б) для частоты ω.
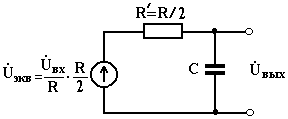
 ∙ C =
∙ C =  ∙ 4 ∙10-6 = 2∙10-5 c.
∙ 4 ∙10-6 = 2∙10-5 c. =
= 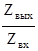 =
= 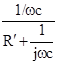 =
= 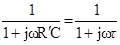 .
. , используя правило определения модуля для дроби, т.е.
, используя правило определения модуля для дроби, т.е.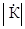 =
= 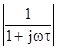 =
= 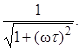



 , а xL=ωL, то можно записать, что
, а xL=ωL, то можно записать, что
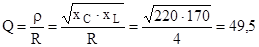 .
.