
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эксплуатационные коэффициенты надежности.Содержание книги Поиск на нашем сайте
Коэффициент использования - это отношение суммарного времени исправной работы системы к общему времени исправной работы и простоя за тот же календарный срок. где ti- время исправной работы между i-1 и i остановками; n- число перерывов в работе за рассматриваемый промежуток времени, включая отказы и профилактические остановки; tni- время вынужденной остановки (простоя). Время простоя включает в себя время профилактики, регулировки, устранения отказов и т.д., но время нахождения аппаратуры в резерве или хранения, а также при отсутствии работы не учитывается. Коэффициент готовности отличается от коэффициента использования тем, что при его определении учитывается не всю время вынужденных простоев, а лишь та часть его, которая затрачивается на поиск и устранение отказа., т.е. Кт есть отношение суммарного времени исправной работы к общему времени исправной работы и восстановления, взятых за один и тот же период: Коэффициент простоя - отношение суммарного времени вынужденных простоев из-за отказов и профилактик к общему времени простоев и исправной работы: Коэффициент стоимости эксплуатации - отношение стоимости годовой эксплуатации к покупной стоимости аппаратуры. Оценка надёжности технических устройств по результатам их испытаний. Контрольные испытания проводятся с целью проверки фактического уровня надёжности испытуемых изделий заданным требованиям. Контроль надежности осуществляется при использовании выборочного метода, при котором заключение о надёжности партии изделий делают по результатам испытаний малой части партии.
1 из возможных процедур: выборка n из партии N изделий ставится на испытания в течении t часов. Фиксируется число отказов r, это число сравнивается с заранее назначенным допустимым числом отказов c. В результате сравнения – вывод: 1) проверенный показатель надёжности изделий соответствует требованиям, и партия принята c≥r. 2) партия не принята c<r. Исход – случайный характер, т.е. есть вероятность того, что P(r≤c) партия будет принята или забракована. Они зависят от надёжности испытываемых изделий. Из-за этой случайности выводы сделанные по результатам испытаний могут быть ошибочными, при этом возникают ошибки 1 и 2-го рода. 1 рода – хорошая партия, бракуется. Причина ошибки неудачный выбор изделий для испытаний. Риск поставщика – α: вероятность ошибки первого рода. 2 рода – принята плохая партия изделий. Причина аналогична. Риск заказчика – β: вероятность ошибки второго рода.
18. Критерии согласия. Критерий Пирсона. Наиболее широко испытываются критерии согласия Пирсона. В этом случае проверка допустимости распределения проверяется следующим образом. Допустим, что в результате испытаний получена гистограмма и получена гипотеза о распределении отказов. Имея такие результаты, строится таблица следующего вида.
Где k- число интервалов; t1,t2,…,tk -середины соответствующих интервалов времени испытаний. Δn*1,… Δn*k- число отказов в соответствующем интервале, полученных в результате испытаний; Δqi*=Δn*I/N- относительная частота отказов в интервале (статистический элемент вероятности отказа) Δqi=ti-1∫ti f(t)dt; Δq1=0∫t1f(t)dt; Δq2=t1∫t2f(t)dt Определения теоретического числа отказов в каждом интервале: Δni = Δqi*N. Затем находиться мера расхождения χi2: χi2=(Δni*-Δni)2/Δni; χ2=i=1∑k [(Δni*-Δni)2/Δni] На следующем этапе определяется число степеней свободы – как разность между числом интервалов и числом наложенных связей. Число наложенных связей S зависит от вида закона, определенный по требованию совпадений основных показателей распределения. i=1∑k Δqi =1
р(χ2 <Δ<∞)=x∫∞ Kr(U)dU, где Δ- мера расхождения; χ2- функция плотности распределения.
Так же может быть критерий Колмогорова и Романовского: R=| χ2 –r|/√2r, Где r число степеней свободы. Если R<3, то гипотеза принимается. Критерий Колмогорова один из наиболее простых. При этом критерий непосредственно на графике плотности распределения находится максимально расположения D между теоретическим расхождением и статистическим. И если D *√n≤1, где n число отказов, то гипотеза принимается. Недостаток этого метода в том, что необходимо знать параметры теоретического закона распределения.
|
||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 601; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.101.51 (0.007 с.) |

 ,
, , где n- число отказов за рассматриваемый промежуток времени. Этот критерий осуществляет одновременно надежность и ремонтопригодность аппаратуры. Если числитель и знаменатель разделить на n, то получим в числителе наработку на отказ,а в знаменателе- наработку на отказ и среднее время восстановления:
, где n- число отказов за рассматриваемый промежуток времени. Этот критерий осуществляет одновременно надежность и ремонтопригодность аппаратуры. Если числитель и знаменатель разделить на n, то получим в числителе наработку на отказ,а в знаменателе- наработку на отказ и среднее время восстановления:  . С точки зрения эксплуатации безразлично, какая аппаратура лучше, высоконадежная, ремонтируется дольше или низконадежная, но ремонтируется легко и быстро.
. С точки зрения эксплуатации безразлично, какая аппаратура лучше, высоконадежная, ремонтируется дольше или низконадежная, но ремонтируется легко и быстро. . Коэффициент простоя - критерий, характеризующий непроизводственные затраты, т.е. затраты на ремонт и профилактику. Кп=1-Ки.
. Коэффициент простоя - критерий, характеризующий непроизводственные затраты, т.е. затраты на ремонт и профилактику. Кп=1-Ки.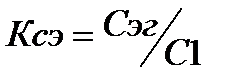 . Для военной аппаратуры Ксэ=2, для гражданской меньше.
. Для военной аппаратуры Ксэ=2, для гражданской меньше. Затем налаживается ограничение на совпадение теоретических и статистических среднего То* = То при экспоненциальном законе. Обычно накладывается 3 ограничения, при экспоненциальном - 2. Число степей свободы r = K-S, где К- число разрядов. Затем по таблице χ2 распределяется определенными квантили распределения χ2. Квантилем случайные величины Х называется такое значение случайных величин Хр, для которого с вероятностью 1-р можно утверждать что полученное значение этой случайной велечены попадает в интервал от (-∞ до Хр). Затем определить вероятность
Затем налаживается ограничение на совпадение теоретических и статистических среднего То* = То при экспоненциальном законе. Обычно накладывается 3 ограничения, при экспоненциальном - 2. Число степей свободы r = K-S, где К- число разрядов. Затем по таблице χ2 распределяется определенными квантили распределения χ2. Квантилем случайные величины Х называется такое значение случайных величин Хр, для которого с вероятностью 1-р можно утверждать что полученное значение этой случайной велечены попадает в интервал от (-∞ до Хр). Затем определить вероятность Г- гамма ф-я (по справочн). Если Р(χ2≤Δ<∞)<0,1, то следует считать что теоретический закон распределения выработан неудачно, то есть гипотеза не подтвердилась. В противном случае следует считать, что выработанное распределение согласуется с экспериментальным и может быть принято.
Г- гамма ф-я (по справочн). Если Р(χ2≤Δ<∞)<0,1, то следует считать что теоретический закон распределения выработан неудачно, то есть гипотеза не подтвердилась. В противном случае следует считать, что выработанное распределение согласуется с экспериментальным и может быть принято.


