
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Ентропійний метод розрахунку стандартної зміни енергії ГіббсаСодержание книги
Поиск на нашем сайте
Розрахунок В його основі лежить відоме термодинамічне рівняння Гіббса-Гельмгольца:
Вихідними даними для розрахунку служать стандартні теплоти утворення На першому етапі за формулами (4.4) и (4.10) визначають тепловий ефект і зміну ентропії реакції в стандартних умовах. Далі за рівняннями (4.8) та (4.11) виконують перерахунок цих величин з температури 298 К на будь яку іншу температуру. Якщо в досліджуваному інтервалі температур учасники реакції мають фазові перетворення, то інтервал інтегрування розбивається на окремі ділянки згідно виразів (4.9) і (4.12). Розрахунок енергії Гіббса можна провести в трьох наближеннях. В першому, самому грубому, наближенні (за стандартними даними для базової температури 298 К) зневажають температурною залежністю термодинамічних функцій, тобто приймають
Через це рівняння оцінюють можливість самовільного протікання хімічної реакції або фазового перетворення з припущенням, що для реакції сума зміни теплоємностей Наступне наближення засновано на тому положенні, що в широкому температурному інтервалі (298... Т) враховується температурна залежність
Для різних випадків застосовують різні наближення. У другому наближенні (за середніми теплоємкостями
Можливість похибки виникає у зв’язку з тим, що криволінійні залежності теплоємності від температури замінюються на прямолінійні залежності, що відповідно відображається у значенні
Друге наближення ентропійного методу в літературі відомо під назвою наближення Уліха, котрий надав останній формулі вигляд:
Позначивши множник Таким чином, розрахунок енергії Гіббса реакції за методом Уліха ведеться за формулою:
Таблиця 5.1. Функція Уліха
В третьому, найбільш точному наближенні – методі розкриття інтегралів, що входять до рівняння (5.4) – враховують температурну залежність термодинамічних функцій, тобто використовують
Виключення інтегральних величин
Приклад. Визначити стандартну зміну енергії Гіббса при температурі 1000 К для реакції
Розрахунок будемо вести ентропійним методом (вихідні дані наведено в табл. 5.2). Таблиця 5.2. Термодинамічні властивості речовин, що входять до реакції
Спочатку визначаємо термодинамічні характеристики реакції в стандартних умовах. Тепловий ефект реакції при 298 К:
Зміна ентропії реакції при 298 К:
З урахуванням точності вихідних даних результат зкруглено до десятих Дж/К. а) перше наближення. Вважаємо
б) друге наближення. Для розрахунку за другим наближенням слід підрахувати алгебраїчну суму теплоємностей для 298 К:
Таким чином, за другим наближенням:
До цього ж результату можна було прийти більш коротким шляхом, використовуючи формулу (5.4) і значення функції Уліха для 1000 К (508.3), визначене з табл. 5.1:
в) третє наближення. За допомогою формули (4.8) розрахуємо теплоємності
Тоді:
Тобто по мірі уточнення чисельне значення Якщо в розглядуваному інтервалі температур речовини, що приймають участь в реакції, не мають фазових перетворень, розрахунок ентропійним методом значно полегшують допоміжні таблиці, складені М. І. Темкіним та Л.А. Шварцманом. В основі цих таблиць покладено наступні теоретичні міркування. В формулі для зміни енергії Гіббса хімічної реакції
Останні дві складові можна поєднати в одну, використовуючи формулу інтегрування по частинам. Якщо прийняти
Таким чином,
Тоді:
Звідки третій і п’ятий члени правої частини рівняння скорочуються. Розділивши всі члени на Т, матимемо:
Як видно, останній член правої частини рівняння дає поправку до результатів наближеного розрахунку. Введемо позначення
Тоді при
а при
Якщо теплоємність речовин, що приймають участь в реакції виражено за допомогою формул
де Величини М 0, М 1, М 2, М -2 для різних температур розраховані М.І. Темкіним и Л.А.Шварцманом и зведені до таблиці 5.3. Таблиця 5.3. Величини
Приклад. Розрахувати Т = 400 К и Р= 1,01 105 Па методом Темкіна – Шварцмана. Дані, необхідні для розрахунку
Зміна ентропії:
Температурні коефіцієнти рівняння (5.13) при 400 К складають:
Алгебраїчні суми температурних коефіцієнтів теплоємностей:
Розрахуємо за рівнянням (5.13)
Вихідні дані для розрахунків та варіанти завдань наведені в таблицях 1.7-1.11, додатку 1. Практичне заняття 6 Явище дифузії в твердих тілах
Загальні положення Внаслідок флуктуації теплової енергії деякі атоми в твердому тілі можуть отримувати енергію більшу за середнє значення. Такі атоми здатні долати потенціальні бар'єри, що утримують їх в рівноважних положеннях в кристалі. Таким чином, атоми в твердому тілі мають здатність переміщуватись – дифундувати, зі швидкістю, що збільшується зі збільшенням температури. Дифузія – поширення речовини в якому - не будь напрямку зниження його концентрації, обумовленої тепловим рухом атомів, молекул, іонів та інших більш крупних частинок.
Дифузія можлива після змочування і розтікання рідкої фази по поверхні твердого тіла. Дифузійні процеси класифікують декількома способами. Розрізняють самодифузію та гетеродифузію. Ефект самодифузії складається із флуктуаційних стрибків однорідних атомів, які відбуваються за відсутності градієнту концентрації. Гетеродифузія – ефект переміщення хімічно різнорідних атомів.
Закони дифузії Фіка Перший закон Фіка. Дифузія спостерігається при нерівномірному розподіленні дифундуючих компонентів в матеріалі – внаслідок чого може бути отриманий пучок атомів через наявність градієнту концентрацій або хімічного потенціалу. Цей процес відбувається на границі 2 фаз і складається з переходу через границю фаз. Потік через задану площину пропорційний градієнту концентрації. Якщо градієнт концентрації першого компоненту напрямлений по осі х, то потік цього компоненту вздовж цієї ж осі (J) рівний:
де D – коефіцієнт дифузії. Це рівняння називають першим законом Фіка. Члени даного рівняння мають наступну розмірність: Перший закон діє для стаціонарного стану. Другий закон Фіка. Якщо стаціонарного стану не досягнуто, тобто концентрація в кожній точці змінюється в залежності від часу, то більш зручно застосовувати інше диференційне рівняння, яке отримується з рівняння (6.1) і балансу речовини. В деякій точці в даний момент часу швидкість зміни концентрації в часі
Це рівняння носить назву другого закону Фіка. Дане рівняння відноситься тільки до одномірної дифузії, а коефіцієнт дифузії не залежить від концентрації і приймає одне і те ж значення в усіх напрямках. Другий закон Фіка, представлений виразом (6.2), можна вивести наступним чином. Розглянемо елемент об’єму товщиною Швидкість накопичення речовини -
Прирівнюючи обидва вирази, отримуємо:
Рис. 6.1. Другий закон Фіка
Саме цей вираз і носить назву другого закону Фіка. Якщо не враховувати деформацію кристалічної гратки та зміну об’єму, викликану дифузією, то коефіцієнт дифузії D не буде залежати від концентрації і, відповідно,
Приклад 6.1. Поверхня нікелевої пластини складається на 50% із Розв’язок. Проведемо розрахунок для елементарної комірки в кожній площині. В г.ц.к. комірці 4 атоми, з них
Так як зміна концентрації між цими точками лінійна, то через будь – яку площину на цій відстані потік атомів, що дифундують буде постійним:
Примітка. Такий потік відповідає приблизно проходженню 9 атомів за 1 с. через кожну елементарну комірку.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 650; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.73.87 (0.012 с.) |

 по стандартним теплотам утворення и стандартним ентропіям речовин, які беруть участь в реакції, використовує абсолютні значення ентропій і стандартні значення цієї величини для багатьох речовин, котрі отримують на основі постулату Планка.
по стандартним теплотам утворення и стандартним ентропіям речовин, які беруть участь в реакції, використовує абсолютні значення ентропій і стандартні значення цієї величини для багатьох речовин, котрі отримують на основі постулату Планка. (5.2)
(5.2)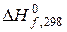 , стандартні ентропії
, стандартні ентропії  и теплоємності речовин, які приймають участь в реакції.
и теплоємності речовин, які приймають участь в реакції. . Тоді
. Тоді (5.3)
(5.3) близька до нуля і не залежить від температури. Таку оцінку можна зробити для інтервалу температур від 298 К до температури зміни агрегатного стану хоча б одного компоненту реакції. Зневага величиною
близька до нуля і не залежить від температури. Таку оцінку можна зробити для інтервалу температур від 298 К до температури зміни агрегатного стану хоча б одного компоненту реакції. Зневага величиною  . Похибка, яка при цьому виникає, залежить від співвідношення величини
. Похибка, яка при цьому виникає, залежить від співвідношення величини  і різниці інтегралів рівняння (5.2), (5.3), де враховується температурна залежність теплоємності.
і різниці інтегралів рівняння (5.2), (5.3), де враховується температурна залежність теплоємності.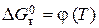 у вигляді рівняння:
у вигляді рівняння: (5.4)
(5.4) для інтервалу (298... Т)) вважають
для інтервалу (298... Т)) вважають  . Тоді:
. Тоді: (5.5)
(5.5) (5.6)
(5.6) , Уліх розрахував його чисельне значення. Добуток
, Уліх розрахував його чисельне значення. Добуток  називають функцією Уліха (табл. 5.1).
називають функцією Уліха (табл. 5.1).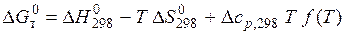 (5.7)
(5.7)

 як функцію температури:
як функцію температури: (5.8)
(5.8)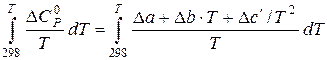
 або
або 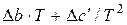 декілька спрощує розрахунки, але похибка при цьому збільшується.
декілька спрощує розрахунки, але похибка при цьому збільшується.
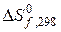 , кДж/моль
, кДж/моль
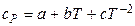 ,
,

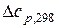
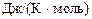

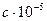

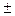 3,4
3,4
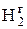




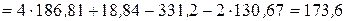 Дж/К
Дж/К , тоді маємо:
, тоді маємо: ,
,  ,
, 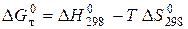
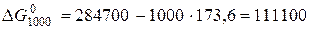 Дж.
Дж.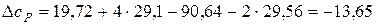 Дж/К
Дж/К Дж
Дж Дж/К
Дж/К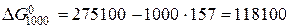 Дж
Дж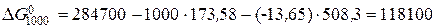 Дж
Дж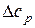 , як функції температури, використовуючи для кожної речовини відповідний температурний ряд:
, як функції температури, використовуючи для кожної речовини відповідний температурний ряд: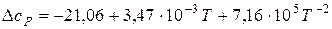 , Дж/К
, Дж/К
 Дж
Дж
 Дж/К
Дж/К Дж
Дж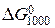 змінюється наступним чином: за першим наближенням воно дорівнює 111100 Дж, за другим – 118100 Дж, і за третім – 119000 Дж.
змінюється наступним чином: за першим наближенням воно дорівнює 111100 Дж, за другим – 118100 Дж, і за третім – 119000 Дж.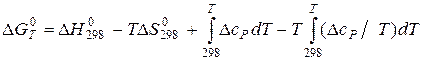 (5.9)
(5.9)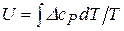 ,
,  то:
то: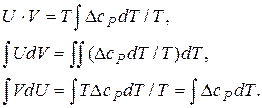
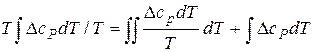 .
.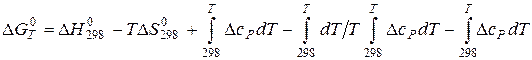 (5.10)
(5.10)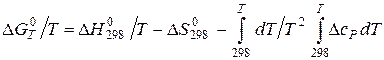 (5.11)
(5.11)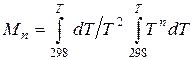 (5.12)
(5.12)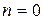 :
: 
 :
: 
 або
або  то:
то: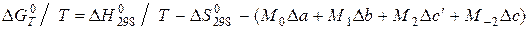 (5.13)
(5.13) – алгебраїчні суми коефіцієнтів в температурному ряді теплоємності, визначені згідно з формулою (4.8).
– алгебраїчні суми коефіцієнтів в температурному ряді теплоємності, визначені згідно з формулою (4.8). для розрахунку термодинамічних функцій за методом Темкіна і Шварцмана
для розрахунку термодинамічних функцій за методом Темкіна і Шварцмана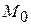
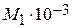
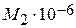



 для реакції
для реакції  при
при , наведені в ході розрахунку. Тепловий ефект реакції при 298 К:
, наведені в ході розрахунку. Тепловий ефект реакції при 298 К: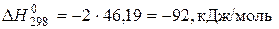 .
.
 = 0,0392;
= 0,0392;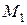 ×10-3 = 0,130;
×10-3 = 0,130; ×105 = 0,036.
×105 = 0,036.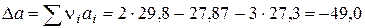




 Дж
Дж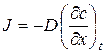 (6.1)
(6.1)
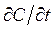 пов’язана з другою похідною градієнту концентрації через коефіцієнт дифузії:
пов’язана з другою похідною градієнту концентрації через коефіцієнт дифузії: (6.2)
(6.2)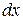 з одиничною площею, який знаходиться в точці х дифузійної зони, рис.6.1. Швидкість накопичення речовини в цій зоні рівна швидкості збільшення концентрації в часі
з одиничною площею, який знаходиться в точці х дифузійної зони, рис.6.1. Швидкість накопичення речовини в цій зоні рівна швидкості збільшення концентрації в часі 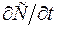 , помноженої на елементарний об’єм.
, помноженої на елементарний об’єм.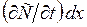 . Ця швидкість накопичення також рівна різниці потоків – того, що входить в розглядуваний об’єм
. Ця швидкість накопичення також рівна різниці потоків – того, що входить в розглядуваний об’єм  і того, що виходить
і того, що виходить  , тобто,
, тобто,

 , або
, або 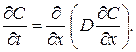
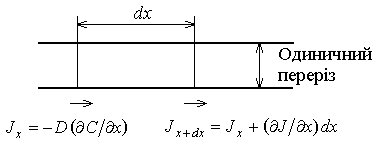
 - одномірне рівняння дифузії.
- одномірне рівняння дифузії. та на 50% із нерадіоактивного нікелю. На відстані 4 мкм від цієї поверхні співвідношення атомних концентрацій
та на 50% із нерадіоактивного нікелю. На відстані 4 мкм від цієї поверхні співвідношення атомних концентрацій 
 при 1000 °С. Визначити потік атомів нікелю через площину, яка знаходиться відстані
при 1000 °С. Визначити потік атомів нікелю через площину, яка знаходиться відстані 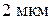 від поверхні. Період гратки (а) нікелю при 1000 °С рівний 3,6 А.
від поверхні. Період гратки (а) нікелю при 1000 °С рівний 3,6 А. атомів
атомів 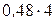 атоми
атоми  рівний (3,6 А)3. Концентрацією є співвідношення кількості атомів в одиниці об’єму, тобто:
рівний (3,6 А)3. Концентрацією є співвідношення кількості атомів в одиниці об’єму, тобто: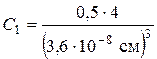 ;
;  .
.
 .
.


