
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Використання основної властивості пропорції при розв’язуванні рівнянь.Содержание книги
Поиск на нашем сайте
Використовуючи основну властивість пропорції, можна знайти її невідомий член, якщо всі інші члени відомі. Приклад. Розв’яжіть рівняння: Розв’язання. 1) Маємо
2) Отримаємо
Прямо пропорційна залежність. Дві змінні величини, відношення відповідних значень яких є сталим, називається прямо пропорційними. Якщо дві величини прямо пропорційні, то із збільшенням (зменшенням) значення однієї з них у кілька разів, значення другої величини збільшується (зменшується) у стільки ж разів. тобто ці величини можна записати як Прямо пропорційними величинами є, наприклад: вартість товару і його кількість; шлях, пройдений тілом із сталою швидкістю і час; периметр квадрата і довжина його сторони тощо. Задачі на прямо пропорційні величини можна розв’язувати за допомогою пропорції. Щоб поділити деяке число s пропорційно заданим числам a та b (розділити в заданому відношенні), треба розділити це число на суму заданих чисел і результат помножити на кожне з них: Приклад. За 2,5 год. автомобіль проїхав 170 км. Яку відстань проїде автомобіль за 4,5 год., якщо швидкість його є сталою? Розв’язання. Запишемо умову задачі схематично: 2.5 год. - 170 км; 4.5 год. - х км. За умовою задачі запишемо пропорцію:
та розв’яжемо утворене рівняння. 2,5х = 170 ∙ 4,5; 2,5x = 765; х = 306. Відповідь: 306 км. Очевидно, що чим більше людей думають про те, щоб прибрати в будинку, тим менше часу треба буде. Якщо самому треба 10 год, то вдвох — 5 год, в трьох — 31/3 год і т. д. Кількість людей, які прибирають, і час, — обернено пропорційні величини. Дві величини обернено пропорційні, якщо, коли помножити на якесь число першу, то друга помножиться на обернений дріб. Перетворення звичайного дробу у десятковий. Оскільки Наприклад:
Перетворення звичайного дробу у нескінчений періодичний десятковий дріб. Якщо спробувати перетворити дріб 9/11 на десятковий, то отримаємо 9/11 = 9: 11 = 0,818181... Крапки в кінці показують, що ділення не закінчилося. Отримали нескінчений десятковий періодичний дріб. Цифри 8 та 1, які стоять поряд у запису нескінченого десяткового дробу і повторюються підряд безліч разів, утворюють період нескінченого періодичного дробу. Це записують так:
Приклади:
Відсотки Соту частину будь-якої величини або числа називають відсотком (процентом). Це слово замінюють знаком %. Щоб записати десятковий дріб за допомогою відсотків, його треба помножити на 100. Щоб перетворити відсотки на десятковий дріб, треба число відсотків розділити на 100. Є три основні задачі на відсотки: 1. Знаходження частини b за відомим її відсотком q від даного числа a. Приклад. Знайти 30% від числа 180
2. Знаходження всього числа а за відомою частиною b і числом відповідних відсотків q. Приклад. Знайти число, 20% якого складає 24 3. Відсоткове відношення числа а до числа b можна знайти за формулою
Приклад 1. Скільки процентів складає число 0,5 від 20? Приклад 2. У 200 г розчину міститься 10 г солі. Який відсотковий вміст солі в розчині? Розв’язання. Приклад 3. Ціна деякого товару знизилася з 60 грн. до 54 грн. на скільки відсотків знизилася ціна товару? Розв’язання. Спочатку знайдемо, на скільки гривень знизилася ціна за товар: 60 - 54 = 6 (грн.). Щоб знайти на скільки відсотків знизилася ціна товару, необхідно знайти відсоткове відношення 6 грн. до початкової ціни товару, тобто 60 грн. Маємо:
Отже, ціна товару знизилася на 10%. Відповідь: на 10%. Приклад 4. Ставка прибуткового податку в Україні дорівнює 15%. Який прибутковий податок треба заплатити із зарплати 2400 грн.? Розв’язання. 15% = 0,15. Тому прибутковий податок складе 2400 ∙ 0,15 = 360 (грн.). Формула складних відсотків. Початковий капітал А0, покладено у банк під р% річних, через n років стане нарощеним капіталом Аn, що обчислюється за формулою:
Цю формулу називають формулою складних відсотків. Відсоткові гроші (прибуток вкладника) можна знайти як різницю Аn - А0. Приклад 1. Вкладник поклав до банку 10000 грн. під 16% річних. Скільки грошей буде на рахунку вкладника через 2 роки? Скільки відсоткових грошей отримає вкладник через 2 роки? Розв’язання. А0 = 10000; р = 16%; n = 2. Маємо
Вкладник отримає таку кількість відсоткових грошей А2 – А0 = 13456 -10000 = 3456 (грн.). Відповідь: 3456 грн. За формулою складних відсотків можна розв’язувати також задачі, не пов’язані з нарощенням капіталу.
Приклад 2. Населення деякого міста становить 50000 мешканців. Кожного року населення зменшується на 0,3%. яким буде населення цього міста через 6 років? Розв’язання. Оскільки населення міста щороку зменшується на один і той самий відсоток, і це відсоток до кількості населення попереднього року, а не до початкової кількості мешканців, то можна використати формулу складних відсотків. Маємо А0 = 50000; р = -0,3 (оскільки населення зменшується, то р < 0); n = 6. Тоді Проміле (‰) — одна тисячна частина якої-небудь величини. Позначається символом ‰. 1‰=10-3=0,001=0,1%. В проміле визначають солоність води, нахил річки, вміст алкоголю в крові, тощо.
|
||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 521; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.188.218.103 (0.01 с.) |


 Відповідь: 9,6.
Відповідь: 9,6. Відповідь: 1,5.
Відповідь: 1,5. , де k — коефіцієнт пропорційності.
, де k — коефіцієнт пропорційності.
 то щоб перетворити звичайних дріб у десятковий, досить чисельник поділити на знаменник.
то щоб перетворити звичайних дріб у десятковий, досить чисельник поділити на знаменник.




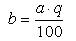




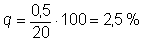
 Відповідь: 5%
Відповідь: 5%


 Відповідь: 49107 чоловік.
Відповідь: 49107 чоловік.


