Награда (от меньшей к большей)

Уровень 1	Уровень 2	Уровень 3	Уровень 4	Уровень 5	Уровень 6
Ответ

 

Источник дисперсии	СК	df	СКВ	F	p
Между уровнями	590,8		118,16	12,64	<0,01
Внутри уровней	224,4		9,35
Общая

Статистическая таблица 3

Критические значения F для отвержения нуль-гипотезы (верхнее число для α — 0.05, а нижнее для α = 0,01)

Степени свободы для знаменателя	Степени свободы для числителя
	18,51	19,00	19,16	19,25	19,30	19,33	19,36	19,37	19,38	19,39
	98,49	99,01	99,17	99,25	99,30	99,33	99,34	99,36	99,38	99,40
	10,13	9,55	9,28	9,12	9,01	8,94	8,88	8,84	8,81	8,78
	34,12	30,81	29,46	28,71	28,24	27,91	27,67	27,49	27,34	27,23
	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04	6,00	5,96
	21,20	18,00	16,69	15,98	15,52	15,21	14,98	14,80	14,66	14,54
	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82	4,78	4,74
	16,26	13,27	12,06	11,39	10,97	10,67	10,45	10,27	10,15	10,05
	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15	4,10	4,06
	13,74	10,92	9,78	9,15	8,75	8,47	8,26	8,10	7,98	7,87
	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73	3,68	3,63
	12,25	9,55	8,45	7,85	7,46	7,19	7,00	6,84	6,71	6,62
	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44	3,39	3,34
	11,26	8,65	7,59	7,01	6,63	6,37	6,19	6,03	5,91	5,82
	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,23	3,18	3,13
	10,56	8,02	6,99	6,42	6,06	5,80	5,62	5,47	5,35	5,26
	4,96	4,10	3,71	3,48	3,33	3,22	3,14	3,07	3,02	2,97
	10,04	7,56	6,55	5,99	5,64	5,39	5,21	5,06	4,95	4,85
	4,84	3,98	3,59	3,36	3,20	3,09	3,01	2,95	2,90	2,86
	9,65	7,20	6,22	5,67	5,32	5,07	4,88	4,74	4,63	4,54
	4,75	3,88	3,49	3,26	3,11	3,00	2,92	2,85	2,80	2,76
	9,33	6,93	5,95	5,41	5,06	4,82	4,65	4,50	4,39	4,30
	4,67	3,80	3,41	3,18	3,02	2,92	2,84	2,77	2,72	2,67
	9,97	6,70	5,74	5,20	4,86	4,62	4,44	4,30	4,19	4,10
	4,60	3,74	3,34	3,11	2,96	2,85	2,77	2,70	2,65	2,60
	8,86	6,51	5,56	5,03	4,69	4,46	4,28	4,14	4,03	3,94
	4,54	3,68	3,29	3,06	2,90	2,79	2,70	2,64	2,59	2,55
	8,68	6,36	5,42	4,89	4,56	4,32	4,14	4,00	3,89	3,80
	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59	2,54	2,40
	8,53	6,23	5,29	4,77	4,44	4,20	4,03	3,89	3,78	3,69
	4,45	3,69	3,20	2,96	2,81	2,70	2,62	2,55	2,50	2,45
	8,40	6,11	5,18	4,67	4,34	4,10	3,93	3,79	3,68	3,59
	4,41	3,55	3,16	2,93	2,77	2,66	2,58	2,51	2,46	2,41
	8,28	6,01	5,09	4,58	4,25	4,01	3,85	3,71	3,60	3,51
	4,38	3,52	3,13	2,90	2,74	2,63	2,55	2,48	2,43	2,38
	8,18	5,93	5,01	4,50	4,17	3,94	3,77	3,63	3,52	3,43
	4,35	3,49	3,10	2,87	2,71	2,60	2,52	2,45	2,40	2,35
	8,10	5,85	4,94	4,43	4,10	3,87	3,71	3,56	3,45	3,37
	4,32	3,47	3,07	2,84	2,68	2,57	2,49	2,42	2,37	2,32
	8,02	5,78	4,87	4,37	4,04	3,81	3,65	3,51	3,40	3,31
	4,30	3,44	3,05	2,82	2,66	2,55	2,47	2,40	2,35	2,30
	7,94	5,72	4,82	4,31	3,99	3,76	3,59	3,45	3,35	3,26
	4,28	3,42	3,03	2,80	2,64	2,53	2,45	2,38	2,32	2,28
	7,88	5,66	4,76	4,26	3,94	3,71	3,54	3,41	3,30	3,21
	4,26	3,40	3,01	2,78	2,62	2,51	2,43	2,36	2,30	2,26
	7,82	5,61	4,72	4,22	3,90	3,67	3,50	3,36	3,25	3,17
	4,24	3,38	2,99	2,76	2,60	2,49	2,41	2,34	2,28	2,24
	7,77	5,57	4,68	4,18	3,86	3,63	3,46	3,32	3,21	3,13
	4,22	3,37	2,98	2,74	2,59	2,47	2,39	2,32	2,27	2,22
	7,72	5,53	4,64	4,14	3,82	3,59	3,42	3,29	3,17	3,09

 

 

2. Кількісні та якісні незалежні змінні. Гіпотеза стосовно максимальної (чи мінімальної) величини.

(Готтсданкер Р. Основы психологического эксперимента / Р. Готтсданкер. – М., 1982. – С. 275-283.)

 

3. Аналіз експерименту «Активізація переживань, пов’язаних з коханням, при спробі пригнічення пригадувань про них».

(Солсо Р.Л., Джонсон Х.Х., Бил М.К. Экспериментальная психология: практический курс. – СПб. – 2002. – С. 290-296.)

 

4. Аналіз експерименту «Просоціальна поведінка».

(Солсо Р.Л., Джонсон Х.Х., Бил М.К. Экспериментальная психология: практический курс. – СПб. – 2002. – С. 420-430.)

 

5. Аналіз експерименту «Алкоголь та презервативи».

(Солсо Р.Л., Джонсон Х.Х., Бил М.К. Экспериментальная психология: практический курс. – СПб. – 2002. – С. 431-454.)

 

6. Гіпотези про абсолютні та відносні відношення.

(Готтсданкер Р. Основы психологического эксперимента. – М., 1982. – С 283-291.)

Многоуровневые независимые переменные позволяют проверять более детализованные экспериментальные гипотезы. Последние создаются на основе моделей и теорий, объясняющих, каким образом ступенчатые изменения независимой переменной приводят к изменению зависимой переменной. Во всех случаях результаты подтверждали гипотезу: при выборе на осях соответствующих шкал получалась линейная зависимость между независимой и зависимой переменной.

В экспериментах экспериментальная гипотеза может состоять в том, что зависимая переменная должна изменяться постепенно по мере постепенного изменения независимой переменной. Однако предполагаемые гипотезой отношения во всех случаях различны.

Любое изменение можно представить либо в абсолютных величинах (на сколько-то единиц), либо пропорциональных/относительных ( во сколько-то единиц ). Так, увеличение от 4 до 6 может быть описано как абсолютное увеличение на 2 или как относительное увеличение в 0,5 (т. е. 6 единиц на 50% больше, чем 4 единицы).

В экспериментах предполагается, что равные абсолютные изменения независимой переменной будут приводить к равным абсолютным изменениям зависимой переменной; равные относительные изменения независимой переменной будут приводить к равным абсолютным изменениям зависимой переменной; равные относительные изменения независимой переменной будут иметь результатом равные относительные изменения зависимой переменной.

Эксперимент с гипотезой «абсолютно-абсолютного» отношения: исследование запоминания; гипотезой «относительно-абсолютного» отношения: реакция выбора; гипотезой «относительно-относительное»: субъективная тяжесть. В каждом из этих трех экспериментов проверявшаяся гипотеза и полученные результаты отражают глубину понимания существенно большую, чем простое знание переменной, воздействующей на поведение. Благодаря нахождению точного отношения между независимой и зависимой переменными (обе понимались как непрерывные величины) мы смогли проникнуть в механизмы соответствующих процессов.

В трех экспериментах, которые мы обсудим ниже, экспериментальная гипотеза состояла в том, что зависимая переменная должна изменяться постепенно по мере постепенного изменения независимой переменной. Однако предполагаемые гипотезой отношения во всех трех случаях различны. Мы начнем с наи6олее простого отношения и перейдем к наиболее сложному.

 

Любое изменение можно представить либо в абсолютных величинах, либо в пропорциональных (относительных). Так, увеличение от 4 до 6 может быть описано как абсолютное увеличение на 2 или как относительное увеличение в 0,5 (т. е. 6 на 50 процентов больше, чем 1).

 

В первых из трех нижеследующих экспериментов предполагалось, что равные абсолютные изменения независимой переменной будут приводить к равным абсолютным изменениям зависимой переменной. Во втором эксперименте предполагалось, что равные относительные изменения независимой переменной будут приводить к равным абсолютным изменениям зависимой переменной. В третьем эксперименте предполагалось, что равные относительные изменения независимой переменной будут иметь результатом равные относительные изменения зависимой переменной. Все это начинает звучать слишком абстрактно, поэтому перейдем к самим экспериментам.

 

Эксперимент с гипотезой «абсолютно-абсолютного» отношения: исследование запоминания

 

Представим эксперимент, в котором испытуемому на короткое время предъявляется какая-то цифра. Если это одна из двух цифр (скажем, 2 или 5), испытуемый нажимает правую кнопку; если цифра не относится к этому набору, который будет называться позитивным (0, 1, 3, 4, 6, 7, 8 или 9), он нажимает левую кнопку. Время реакции измеряется от момента появления цифры до нажатия на кнопку. В различных сериях используются разные объемы позитивного набора: он может состоять из одной, трех, четырех, пяти или шести цифр. При этом находят среднее время реакции для каждого объема позитивного набора. Затем строится график, выражающий зависимость времени реакции от объема набора. Результаты такого эксперимента (Стернберг, 1969) показаны на рис. 7.4. Как можно видеть, линия, соединяющая все точки, не совершенно прямая. Однако небольшая волнистость скорее всего связана со случайными вариациями. На основании этих результатов мы можем сказать, что для получения одного и того же абсолютного прироста времени реакции (35 мс) уровень независимой переменной (объем набора) должен быть увеличен на одну единицу (снова в абсолютных единицах).

ГИПОТЕЗЫ ОБ АБСОЛЮТНЫХ И ОТНОСИТЕЛЬНЫХ ОТНОШЕНИЯХ Читайте также: IX. Об отношениях человека к Богу АДМИНИСТРАТИВНАЯ ОТВЕТСТВЕННОСТЬ В ИЗБИРАТЕЛЬНЫХ ОТНОШЕНИЯХ Библейские свидетельства о внутрисемейных отношениях Библейские свидетельства о внутрисемейных отношениях Будь постоянен в сексуальных отношениях и браке. Виды и взаимосвязи относительных величин Вправе ли новый должник выдвигать возражения против требований кредитора, основанные на отношениях между кредитором и первоначальным должником       В трех экспериментах, которые мы обсудим ниже, экспериментальная гипотеза состояла в том, что зависимая переменная должна изменяться постепенно по мере постепенного изменения независимой переменной. Однако предполагаемые гипотезой отношения во всех трех случаях различны. Мы начнем с наи6олее простого отношения и перейдем к наиболее сложному.   Любое изменение можно представить либо в абсолютных величинах, либо в пропорциональных (относительных). Так, увеличение от 4 до 6 может быть описано как абсолютное увеличение на 2 или как относительное увеличение в 0,5 (т. е. 6 на 50 процентов больше, чем 1).   В первых из трех нижеследующих экспериментов предполагалось, что равные абсолютные изменения независимой переменной будут приводить к равным абсолютным изменениям зависимой переменной. Во втором эксперименте предполагалось, что равные относительные изменения независимой переменной будут приводить к равным абсолютным изменениям зависимой переменной. В третьем эксперименте предполагалось, что равные относительные изменения независимой переменной будут иметь результатом равные относительные изменения зависимой переменной. Все это начинает звучать слишком абстрактно, поэтому перейдем к самим экспериментам.   Эксперимент с гипотезой «абсолютно-абсолютного» отношения: исследование запоминания   Представим эксперимент, в котором испытуемому на короткое время предъявляется какая-то цифра. Если это одна из двух цифр (скажем, 2 или 5), испытуемый нажимает правую кнопку; если цифра не относится к этому набору, который будет называться позитивным (0, 1, 3, 4, 6, 7, 8 или 9), он нажимает левую кнопку. Время реакции измеряется от момента появления цифры до нажатия на кнопку. В различных сериях используются разные объемы позитивного набора: он может состоять из одной, трех, четырех, пяти или шести цифр. При этом находят среднее время реакции для каждого объема позитивного набора. Затем строится график, выражающий зависимость времени реакции от объема набора. Результаты такого эксперимента (Стернберг, 1969) показаны на рис. 7.4. Как можно видеть, линия, соединяющая все точки, не совершенно прямая. Однако небольшая волнистость скорее всего связана со случайными вариациями. На основании этих результатов мы можем сказать, что для получения одного и того же абсолютного прироста времени реакции (35 мс) уровень независимой переменной (объем набора) должен быть увеличен на одну единицу (снова в абсолютных единицах).   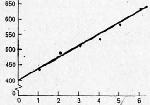Рис. 7.4. Зависимость времени реакции опознания тестового стимула от количества знаков в ранее предъявленном наборе (эксперимент Стернберга, 1972). Ось абсцисс — размер предъявленного набора. Ось ординат — время реакции (мс). Эксперимент с гипотезой «относительно-абсолютного» отношения: реакция выбора   Два экспериментатора, У. Е. Хик в Англии и Рэй Хаймен в США, провели почти в одно и то же время сходные эксперименты в русле так называемого информационного подхода (Хик, 1952; Хаймен, 1953). Для позитивного набора стимулов они нашли иную закономерность между числом альтернатив и временем реакции, чем Стернберг. Методика Хика несколько проще методики Хаймена, поэтому мы приводим ее в качестве примера.   Перед испытуемым полукругом располагалось 10 маленьких электрических лампочек. Его пальцы (включая большие) свободно лежали на десяти телеграфных ключах. Когда зажигалась лампочка, испытуемый должен был нажать соответствующий ключ. Десять альтернатив составляли наиболее высокий уровень независимой переменной. В других условиях могли зажигаться либо 8, либо 6, либо 5, либо 4, либо 3, либо 2, либо даже 1 из 10 лампочек. Каждый новый сигнал появлялся через 5 с после предыдущего ответа.   Специальные серии проб проводились для 1, 2, 3, 4, 5, 6, 8 и 10 альтернатив. Для каждого из этих уровней определялось среднее время реакции. На рис. 7.5 представлена двумя различными способами зависимость между числом альтернатив и временем реакции. В случае (а) шкала независимой переменной (ось абсцисс) является абсолютной, как и для данных Стернберга. На ней одинаковому увеличению числа альтернатив соответствует одинаковое расстояние на шкале. Однако график получился не прямым, а изогнутым книзу. Каждое новое увеличение числа альтернатив на единицу вызывает все меньший прирост времени реакции. Если же ось абсцисс изменить и представить в том виде, как на правом рисунке (б), график выпрямляется. Деления на рис. 7.5 (б) представляют собой шаги в относительных единицах (такая шкала называется логарифмической). Так, на этой шкале каждому удвоению числа альтернатив — от 1 к 2, от 2 к 4, от 3 к 6 — соответствуют одинаковые расстояния. Чтобы удостовериться, измерьте шкалу.   Рис. 7.5. Зависимость времени реакции от количества альтернатив (эксперимент Хика, 1952). Ось абсцисс — количество альтернатив. Ось ординат — время реакции (мс)   Таким образом, прямая линия, представляющая отношение между числом альтернатив и временем реакции, подтверждает гипотезу «относительно-абсолютное». При увеличении числа альтернатив в равном отношении мы получаем равное абсолютное увеличение времени реакции. Удвоение числа альтернатив является относительным увеличением на единицу, т. е. на 100%. Каждое такое удвоение увеличивает время реакции на 110 мс — на одну и ту же абсолютную величину.   Эксперимент с гипотезой «относительно-относительное»: субъективная тяжесть   Чувствует ли человек вес в 200 граммов как половину веса в 400 граммов? Этот вопрос задал себе С. С. Стивенс. Проводя серии экспериментов в течение ряда лет, он использовал не только веса, но также звуковые тоны, свет, запахи и т. д.   Эксперимент с весами был организован Р. Харпером и Стивенсом (1948) очень просто. Испытуемый стоял возле стола, на котором лежали 7 одинаковых закрытых контейнеров. Один из них откладывали в сторону и называли «эталоном». Задача состояла в том, чтобы, взвешивая в руке эталон и каждый из 16 других весов, выбрать тот, который воспринимался как половина веса эталона» (с. 344). Заметьте: испытуемые должны были найти не тот вес, который действительно составлял половину веса эталона, а только ощущался таковым.   Было найдено, чего вес, который воспринимается как в 2 раза более легкий, чем эталон 100 г, в среднем составлял 72 г. Экспериментаторы выразили это отношение следующим образом. Пусть вес 100 г имеет субъективную тяжесть 1 вег (по определению), тогда вес 72 г имеет субъективную тяжесть 1/2 вег. Между прочим, слово «вег» Харпер и Стивене образовали от старого норвежского слова veg — поднимать (с. 345).   В другой серии в качестве эталона использовался вес, отличный от 100 г. Оказалось, что когда в качестве эталона брался вес 140 г, половинное ощущение тяжести соответствовало в среднем 100 г. Поскольку 100 г представлялись как 1 вег, то 140 г было приписано значение тяжести 2 вег.   Всего было 8 серий, в которых эталон изменялся от 20 до 2000 г. В результате всех ответов была получена сглаженная кривая, отражающая отношение между физическими весами и ощущениями их тяжести (рис. 7.6, а).   Можно видеть, что когда горизонтальная и вертикальная оси представлены абсолютными шкалами (например расстояние между 100 и 200 г такое же, как и между 500 и 600 г, а расстояние между 10 и 20 вег такое же, как между 30 и 40), линия не является прямой, а изгибается кверху. Однако когда обе оси были прошкалированы в относительных единицах (например расстояние между 100 и 200 г такое же, как между 400 и 800 г, а расстояние между 2 и 4 вег такое же, как между 8 и 16 вег), результаты очень хорошо легли на прямую (рис 7.6, б).     Рис. 7.6. Изменения в ощущении тяжести с увеличением поднимаемого груза (эксперимент Харпера и Стивенса, 1948). Ось абсцисс - вес груза (г). Ось ординат — ощущение тяжести (в вегах)   Таким образом, была подтверждена гипотеза об «относительно-относительной» зависимости. Каждый раз, когда вы увеличиваете физический вес в определенное число раз, ощущение тяжести также увеличивается в определенное число раз. Следует также заметить, что оси разделены на одинаковые относительные единицы. Например, расстояние между 2 и 4 вег такое же, как между 100 и 200 г. Если относительное увеличение веса дает почти такой же относительный прирост в ощущении тяжести, график зависимости будет иметь угол наклона 45° (как показано пунктирной линией). В данном эксперименте относительное увеличение на единицу (т. е. на 100%) физического веса дает большое относительное увеличение субъективной тяжести – примерно на 2,5 ед. (т. е. на 250%). Другими словами, удвоение физического веса почти учетверяет его субъективную тяжесть.   Возвращаясь к поставленному вначале вопросу, мы теперь можем ответить, что вес 200 г не воспримется как половина веса 400 г: он покажется значительно легче.   Прогресс в понимании   Каждое из трех рассмотренных отношений представляет теорию или модель механизмов, лежащих в основе поведения. Механизм, предполагаемый «абсолютно-абсолютной» гипотезой Стернберга, следующий. Все цифры позитивного набора фиксируются в памяти испытуемого. Когда появляется тестовая цифра, элементы позитивного набора последовательно «сканируются» для определения того, принадлежит данная цифра к позитивному набору или нет. Другими словами, предъявленная цифра по очереди сравнивается с каждым элементом набора. Если на каждое такое сравнение уходит 35 мс, то при добавлении к позитивному набору еще одной цифры общее время сканирования возрастет именно на эту величину. Таким образом, тот факт, что каждое абсолютное увеличение позитивного набора на один элемент сопровождается увеличением времени реакции на одну и ту же абсолютную величину, подтверждает модель последовательного сканирования.   Гипотеза Хика об «относительно-абсолютной» зависимости времени реакции от числа альтернативных наборов вытекает из модели другого типа. Идея ее состоит в том, что испытуемый совершает выбор, применяя стратегию последовательности простых решений. Так, если существует восемь альтернатив, первое простое решение состоит в выборе между альтернативной группой 1, 2, 3, 4 и альтернативной группой 5, 6, 7, 8. Предположим, правильным выбором является альтернатива 7. Тогда первым решением будет выбор группы 5, 6, 7, 8. Следующее простое решение будет состоять в выборе между группами 5, 6 и 7, 8. Правильным вторым простым решением будет группа 7, 8. Остается только выбор между 7 и 8. Третьим и последним простым решением будет выбор альтернативы 7. В целом для восьми альтернатив мы имели только три простых решения. Для различного числа альтернатив будет сохраняться следующее: две альтернативы — одно решение; четыре альтернативы — два решения; восемь альтернатив — три решения и т. д. Если каждое простое решение требует одного и того же количества времени, которое, как здесь установлено, равно 110 мс, то для каждого увеличения числа альтернатив на одну относительную единицу (т. е. на 100%) мы будем иметь одно и то же абсолютное увеличение времени реакции (на 110 мс). Конечно, эта теория должна быть уточнена и для другого числа альтернатив, которое не является степенями двойки, например для шести или десяти.   Гипотеза Стивенса об относительном приросте ощущения при относительном увеличении стимула основывается на его концепции о механизме преобразования физической энергии в сенсорном органе: пропорциональное увеличение энергии стимула дает почти, пропорциональное увеличение нервного возбуждения.   В каждом из этих трех экспериментов проверявшаяся гипотеза и полученные результаты отражают глубину понимания существенно большую, чем простое знание переменной, воздействующей на поведение. Благодаря нахождению точного отношения между независимой и зависимой переменными (обе понимались как непрерывные величины) мы смогли проникнуть в механизмы соответствующих процессов.

В предыдущих главах были описаны две основные экспериментальные схемы. Это — межгрупповая схема, при которой каждое экспериментальное условие предъявляется отдельной группе испытуемых и схема внутрииндивидуальных проверок. Обе эти схемы будут рассмотрены теперь в связи с многоуровневым экспериментом. Из этого анализа будет понятно, почему исследователей привлекает еще одна, третья, основная схема, которая будет описана в следующем разделе.

 

7. Факторні експерименти.

(Готтсданкер Р. Основы психологического эксперимента. – М., 1982. – С 322-326.)

ГЛАВА 8. Факторные эксперименты.

Факторный эксперимент – это эксперимент с использованием по крайней мере двух НП. В итоге факторного эксперимента определяется основной результат действия каждой из НП и взаимодействия между ними. На примере эксперимента с рассеченным сводом раскрыто конкретное содержание основных результатов и взаимодействия и показаны способы их измерения. Основной результат действия НП – разность между средними общими значениями ЗП по каждому из уровней. Взаимодействие – разность между двумя разностями по каждому из уровней второй НП. Одна из НП помещается на горизонтальной оси, и затем по соответствующим значениям ЗП строятся соответствующие графики для каждого из уровней другой НП. Если отрезки, полученные таким образом для второй НП, параллельны, взаимодействие отсутствует. Если отрезки расходятся вправо или влево, взаимодействие называют расходящимся, а если они пересекают друг друга, то это пересекающееся взаимодействие.

При использовании схем позиционного уравнивания эксперимент автоматически становится факторным. Главное преимущество факторных экспериментов – возможность проверять настоящие комбинированные гипотезы.

ЗАКОН ЙЕРКСА-ДОДСОНА

Оптимальная сила напряжения, способствующая хорошему обучению, должна понижаться с увеличением трудности задач.

В факторных экспериментах: взаимодействие между двумя переменными называется взаимодействием первого порядка, между тремя – взаимодействием второго порядка и т.д.

Все экспериментальные схемы можно классифицировать по трем основным параметрам:

1. способ сравнения условий или уровней НП: сравнение по каждому испытуемому, межгрупповое сравнение, или сравнение по всем испытуемым;

2. по характеру изменения НП: качественный или количественный;

число НП: либо эксперимент с одной переменной, либо факторный эксперимент.

(Кравчук С.Л. Експериментальна психологія: теорія та практика психологічного експерименту. – К., 2008. – С. 117-142.)