З курсу «Експериментальна психологія»

Завдання до семінару

З курсу «Експериментальна психологія»

 

1. Поняття «багаторівневий експеримент». Багаторівневий експеримент як контрольний. Кращий контроль над супутнім змішуванням.

(Готтсданкер Р. Основы психологического эксперимента / Р. Готтсданкер. – М., 1982. – С. 267-274.)

МНОГОУРОВНЕВЫЕ ЭКСПЕРИМЕНТЫ

Автор: Роберт Готтсданкер
Опубликовано: January 5, 2007, 12:59 am

Многоуровневый эксперимент как контрольный

Сначала мы рассмотрим, что дает многоуровневый эксперимент, когда экспериментальная гипотеза может быть проверена и с использованием только двух условий. Примером может служить эксперимент по рабочей этике, обсуждавшийся в главе 5, где было показано, что девочки-индианки предпочитают активные усилия безделью. Сравнивались два условия: (1) получение шарика без нажатия на рычаг и (2)получение шарика после 10-кратного нажатия на рычаг. Можно было бы использовать различное число нажатий, например 2, 5, 10, 50 за каждый шарик. Улучшился ли бы эксперимент при введении большого числа уровней настолько, чтобы его стоило проводить? (Хотя, учитывая гипотезу авторов, ответ заранее ясен: многоуровневый эксперимент должен бы предпочитаться исследователями, поскольку он требует больше активных усилий с их стороны.)

Меньше шансов пропустить эффект

Чтобы увидеть преимущество пятиуровневого эксперимента, следует ответить на вопрос, каким образом экспериментаторы узнали, что для одного из двух экспериментальных условий необходимо использовать именно десять нажатий на рычаг. Возможно, — это слишком небольшая работа, чтобы влиять на поведение, а может быть, наоборот, слишком большая. Очевидно, исследователи Сингх и Квери (1971) просто решили, что одного нажатия на шарик будет слишком мало. Точно так же нельзя предлагать очень много нажатий за одни шарик, ибо в этой случае девочки будут, безусловно, стремиться получать шарики просто так, и лишь где-то между этими крайними значениями будет находиться число нажатий (уровень), при котором активное и пассивное условия окажутся одинаково предпочитаемыми. Если бы Сингх и Квери остановили свой выбор на уровне равного предпочтения, они оказались бы в том же положении, что и воображаемый экспериментатор В, чьи результаты показывают, что независимая переменная не оказывает никакого действия. Проделанный сейчас анализ показывает, что гипотеза, проверявшаяся в исследовании Сингха и Квери, в действительности была количественной гипотезой, соотносящей количество нажатий на рычаг с величиной предпочтения активных усилий пассивной награде. Хорошо проверить такую гипотезу можно только при условии, если независимая переменная будет непрерывна. Это, конечно, невозможно, поскольку тогда потребуется бесконечное число уровней с бесконечно малыми различиями. И все же при использовании даже пяти уровней можно приблизиться к выявлению полного отношения между независимой и зависимой переменными. По мере уменьшения числа уровней увеличивается опасность ошибочного представления этого отношения. Поэтому можно сказать, что внутренняя валидность больше, когда такая гипотеза проверяется при пяти уровнях по сравнению с двумя уровнями независимой переменной. Эта угроза внутренней валидности вытекает из неполноты независимой переменной. Угрозы, описанные выше, проистекали либо из ненадежности данных, либо из процедурного или сопутствующего смешения с другими переменными (см. гл. 5, с. 193). Воображаемые эксперименты А, Б и В служат драматическим примером того, как ложно может быть представлено отношение между независимой и зависимой переменными из-за использования небольшого числа уровней. Кроме того, эксперимент с двумя уровнями сталкивается еще с одной проблемой, касающейся сопутствующего смешения. К показу этого мы сейчас и перейдем.

Гипотеза о максимальной (или минимальной) величине

Эксперимент на скорость предъявления и запоминание

Возвратимся снова к эксперименту Калфи и Андерсон (1971), в котором общее время запоминания списка было распределено различным образом. Как можно видеть на рис. 7.1, шесть различных временных интервалов между элементами списка составили шесть уровней независимой переменной. Каждый интервал исследовался для отдельной группы испытуемых в 20 человек. Максимальная величина зависимой переменной — чуть больше 13 правильных ответов — обнаружилась для интервала 4 с, т. е. при пяти повторных предъявлениях списка из 16 элементов в течение 320 секунд экспериментального времени. Этот результат был как раз таким, который ожидали Калфи и Андерсон. Остановимся вкратце на причинах, по которым экспериментальная гипотеза о максимальном значении при одном из промежуточных уровней независимой переменной имеет смысл.

Прогресс в понимании

Существует множество экспериментов, в которых гипотеза максимума или минимума вполне оправдана. Между прочим, не нужно считать, что термины максимум и минимум означают в этих экспериментах разное. Бели бы в эксперименте Йеркса и Додсона мерой научения служило число правильных ответов, то при 300 единицах стимуляции достигался бы максимум. Если бы Калфи и Андерсон использовали в качестве зависимой переменной среднее число ошибок, а не правильных ответов, то при интервале 4 с достигался бы минимум.

Напомним, что количественная гипотеза в эксперименте Сингха и Квери по трудовой этике состояла в том, что предпочтение работы бездеятельности будет расти с увеличением требуемого количества нажатий на рычаг, — но только до определенного предела после того как будет достигнут максимум, дальнейшее увеличение количества нажатий поведет к уменьшению предпочтения этого условия. Основанием для такого предположения была мысль о том, что по мере увеличения необходимого количества нажатий происходят сразу два процесса. Вначале растет «чувство активности» и оно увеличивает привлекательность работы с рычагом. Однако эти усилия не могут быть только приятными; с дальнейшим увеличением числа нажатии возникает и нарастает «неприятное» чувство. Максимальное предпочтение условия с нажатием на рычаг бездеятельному условию будет достигнуто при таком уровне нажатий, когда разница между чувством активности и неприятным чувством будет наибольшей. Итак, одним из оснований гипотезы максимума (или минимума) является теория двух противоположных основных процессов, определяемых независимой переменной. Причем 282«негативный» процесс при достижении независимой переменной высокого уровня становится сильнее «позитивного».

Эксперименты Калфи и Андерсон (1971) с запоминанием демонстрируют другой вид противоположных тенденций. Для того чтобы воспроизводить правильные числа при показе триграмм, испытуемый в первую очередь не должен смешивать сами триграммы. Это называется различением стимулов. Ему способствует уменьшение интервала между элементами списка. Во-вторых, испытуемый должен научиться связывать каждое число с парной ему триграммой. Это называется ассоциативнымпроцессом. Ему способствует увеличение времени между элементами списка. Таким образом, должен существовать оптимальный интервал. Любой более короткий интервал дает выигрыш в различении в ущерб ассоциативному процессу; любой более длинный интервал дает выигрыш в ассоциативном процессе в ущерб различению. Итак, второе основание для ожидания максимума (или минимума) — это теория, согласно которой увеличение независимой переменной вызывает противоположные изменения в двух основных процессах, каждый из которых «положителен». Максимум или минимум достигается при уровне, который дает оптимальное сочетание этих двух процессов.

Можно показать, что танцующая мышь, учившаяся избегать удара током, находилась точно в таком же положении. Она должна была различать два туннеля и ассоциировать туннель с ударом тока или его отсутствием. По свидетельству Йеркса и Додсона (1908, с. 476), различение было плохим при слишком сильном ударе. «Поведение мышей менялось по мере усиления стимуляции. При сильной стимуляции они выбирали не менее быстро, чем при слабой, однако в первом случае они были менее осторожны и действовали с меньшей осмотрительностью и уверенностью». Таким образом, различение стимулов (черного и белого) ухудшалось с увеличением силы удара. Ассоциирование же белого туннеля с ударом (при состоявшемся различении) могло с усилением удара только усиливаться. Следовательно, здесь снова должен был существовать некоторый уровень независимой 283переменной (силы удара), оптимальный для дискриминационного научения.

Наверное некоторые из вас уже предвосхитили дальнейшее рассуждение. Оно состоит в том, что более сложное различение требует большей осторожности и осмотрительности, чем простое. Это означает прежде всего, что оно осваивается медленнее. Более того, оптимальным для его освоения будет удар, более слабый, чем для простого различения. Как раз такие результаты и получили исследователи в своей дальнейшей работе. Вот их заключение: «По мере увеличения сложности различения интенсивность стимула, оптимальная для формирования навыка, приближается к порогу» (1908, с. 481). Эта зависимость сегодня известна под названием закона Йеркса — Додсона. Но мы забежали вперед, к анализу этих экспериментов мы обратимся в следующей главе.

На примере трех описанных исследований было показано, что многоуровневый эксперимент может обеспечить проверку гипотезы о двух процессах, связанных с уровнем независимой переменной противоположным образом. Действительная экспериментальная гипотеза состоит в том, что максимум (или минимум) зависимой переменной будет достигаться при некотором промежуточном уровне независимой.

Прогресс в понимании

Каждое из трех рассмотренных отношений представляет теорию или модель механизмов, лежащих в основе поведения. Механизм, предполагаемый «абсолютно-абсолютной» гипотезой Стернберга, следующий. Все цифры позитивного набора фиксируются в памяти испытуемого. Когда появляется тестовая цифра, элементы позитивного набора последовательно «сканируются» для определения того, принадлежит данная цифра к позитивному набору или нет. Другими словами, предъявленная цифра по очереди сравнивается с каждым элементом набора. Если на каждое такое сравнение уходит 35 мс, то при добавлении к позитивному набору еще одной цифры общее время сканирования возрастет именно на эту величину. Таким образом, тот факт, что каждое абсолютное увеличение позитивного набора на один элемент сопровождается увеличением времени реакции на одну и ту же абсолютную величину, подтверждает модель последовательного сканирования.

Гипотеза Хика об «относительно-абсолютной» зависимости времени реакции от числа альтернативных наборов вытекает из модели другого типа. Идея ее состоит в том, что испытуемый совершает выбор, применяя стратегию последовательности простых решений. Так, если существует восемь альтернатив, первое простое решение состоит в выборе между альтернативной группой 1, 2, 3, 4 и альтернативной группой 5, 6, 7, 8. Предположим, правильным выбором является альтернатива 7. Тогда первым решением будет выбор группы 5, 6, 7, 8. Следующее простое решение будет состоять в выборе между группами 5, 6 и 7, 8. Правильным вторым простым решением будет группа 7, 8. Остается только выбор между 7 и 8. Третьим и последним простым решением будет выбор альтернативы 7. В целом для восьми альтернатив мы имели только три простых решения. Для различного числа альтернатив будет сохраняться следующее: две альтернативы — одно решение; четыре альтернативы — два решения; восемь альтернатив — три решения и т. д. Если каждое простое решение требует одного и того же количества времени, которое, как здесь установлено, равно 110 мс, то для каждого увеличения числа альтернатив на одну относительную единицу (т. е. на 100%) мы будем иметь одно и то же абсолютное увеличение времени реакции (на 110 мс). Конечно, эта теория должна быть уточнена и для другого числа альтернатив, которое не является степенями двойки, например для шести или десяти.

Гипотеза Стивенса об относительном приросте ощущения при относительном увеличении стимула основывается на его концепции о механизме преобразования физической энергии в сенсорном органе: пропорциональное увеличение энергии стимула дает почти, пропорциональное увеличение нервного возбуждения.

В каждом из этих трех экспериментов проверявшаяся гипотеза и полученные результаты отражают глубину 291понимания существенно большую, чем простое знание переменной, воздействующей на поведение. Благодаря нахождению точного отношения между независимой и зависимой переменными (обе понимались как непрерывные величины) мы смогли проникнуть в механизмы соответствующих процессов.

Межгрупповые схемы

Калфи и Андерсон (1971) применили в своих экспериментах на запоминание межгрупповую схему. Они использовали шесть различных интервалов между элементами запоминаемого списка: 1, 2, 3, 4, 10 и 20 с. Каждый интервал предъявлялся отдельно труппе в 20 человек; таким образом, в опытах участвовало всего 120 человек. (И это была только четвертая часть обширного исследования, где в общем участвовало 480 человек!) Испытуемые распределялись по уровням (независимой переменной) случайно, по мере того как они приходили на опыты. Один недостаток использования межгрупповой схемы в многоуровневом эксперименте очевиден сразу. Поскольку для каждого уровня требуется большое количество испытуемых, то (с целью уравнивания групп) общее необходимое количество испытуемых становится нереально большим.

Реверсивное уравнивание

Реверсивное (обратное) уравнивание — это схема, которую мы только что обсуждали. Она может быть представлена следующим образом:

Группа испытуемых	Последовательность условий (уровней)
	ВБАГД (вообще любая)
	ДГАБВ (обратная ей)

Это означает, что используется только две последовательности уровней. Как мы только что показали, они не обязательно должны быть АБВГДЕ и ЕДГВБА, где А означает наименьший уровень независимой переменной и Е — наибольший уровень. Здесь вообще могут быть разные варианты. Например, в другой части экспериментов Готтсданкера и Уэй, о котором говорилось выше, в одном блоке проб временной интервал между двумя стимулами оставался постоянным. Одной группе из четырех испытуемых предъявлялось пять блоков по 100 проб с временными интервалами в следующем порядке: 50, 100, 200, 400 и 800 мс (т. е. АБВГД). Порядок предъявления для другой группы из четырех испытуемых был: 800, 400, 200, 100 и 50 мс (т. е. ДГВБА).

Реверсивное уравнивание обеспечивает для каждого уровня одну и ту же среднюю позицию по двум последовательностям. Так, для двух показанных на диаграмме порядков ВБАГД и ДГАБВ уровень Д находится в позиции 5 и 1 при среднем 3; уровень Г — в позиции 4 и 2 при среднем, снова равном 3, и т. д. Это уравнивание обеспечивает хороший контроль влияния последовательности, только если эффект переноса однороден, т. е. если предполагается, что позиция 1 влияет так же на позицию 2, как позиция 2 на 3, или 3 на 4, или 5 на 6.

Однако эффект переноса может быть неоднороден, как это было показано в главе 2, применительно к внутрииндивидуальной схеме; тогда возникает серьезная проблема. Предположим, что существуют эффекты научения, которые равномерно улучшают ответ вплоть до третьей пробы, но не дальше. Для испытуемых, которым предъявляется последовательность ВБАГД, последние три уровня — А, Г и Д — будут в одинаково «выгодном положении». Для испытуемых, которым предъявляется обратная последовательность ДГАБВ, последние уровни — А, Б и В — будут также в одинаково «выгодном положении». Поэтому уровень А, находящийся в середине обеих последовательностей, будет иметь наибольшее преимущество, а В и Д — наименьшее. Если же эффект переноса связан с утомлением, а не научением, то теперь уровень в середине обеих последовательностей окажется в наиболее неблагоприятном положении.

Если эффект переноса различен в различных последовательностях, то величина переноса оказывается переменной, производящей смешение. В только что разбиравшейся последовательности ВБАГД величина переноса для В равна 0 (поскольку это первое условие), для Б — 1 и для А, Г и Д — 2 (поскольку перенос не увеличивается после третьей пробы). Аналогично для обратной последовательности — ДГАБВ — величины переноса будут: 0 для Д, 1 для Г и 2 для А, Б, В. Общий суммарный эффект переноса будет равен: 4 для А, 3 для Б и Г, 2 для В и Д. Из-за неэффективности в подобных случаях схемы реверсивного уравнивания исследователи обратились к схемам, которые обеспечивают лучший контроль. Они и будут сейчас описаны.

Полное уравнивание

Для того чтобы избежать систематического смешения, возникающего при неоднородном переносе в схеме реверсивного уравнивания, можно использовать все возможные 296последовательности уровней, вместо двух. Такая схема с полным уравниванием для трехуровневого эксперимента выглядит следующим образом:

Группы испытуемых	Последовательности
	АБВ
	АВБ
	БАВ
	БВА
	ВАБ
	ВБА

Так, если бы в исследовании Готтсданкера и Уэй было использовано только три уровня независимой переменной (например 50, 100 и 200 мс), различным испытуемым — или группам испытуемых — были бы предъявлены следующие шесть последовательностей: 50, 100, 200 мс; 50, 200 и 100 мс; 100, 50 и 200 мс; 100, 200 и 50 мс; 200, 50 и 100 мс; 200, 100 и 50 мс. Мы не иллюстрируем полное уравнивание для большего числа уровней независимой переменной (обычно встречающегося в многоуровневых экспериментах) по той причине, что таблица оказалась бы слишком громоздкой. Например, для всех пяти уровней в исследовании Готтсданкера и Уэй потребовалось 120 последовательностей. Так что если бы даже только один испытуемый проводился через одну последовательность, то число испытуемых оказалось бы равным 120. Число последовательностей, необходимых для полного уравнивания, вычисляется как n-факториал, где n — число уровней. Для шести уровней n-факториал находится следующей серией умножений:

6Х5Х4ХЗХ2Х1=720.

Поскольку кросс-индивидуальное уравнивание было введено для сокращения числа испытуемых по сравнению с их числом в межгрупповой схеме, полное позиционное уравнивание используется крайне редко. Нижеследующая схема позволяет сократить число испытуемых, избегая допущения об однородном переносе, необходимом для схемы реверсивного уравнивания.

Латинский квадрат

Если мы не хотим использовать все возможные последовательности, то естественно прийти к идее о случайном выборе из всего их множества. Иногда это и делается. Однако в случайно выбранном наборе последовательностей мало вероятно, что каждый уровень окажется в каждой позиции равное число раз. Поэтому нежелательные последствия неоднородного переноса будут по-прежнему существовать.

Выходом будет случайный выбор среди «квадратов», в которых каждый уровень появляется один раз в каждой позиции. Каждый такой квадрат представляет собой полную экспериментальную схему. Он называется латинским квадратом. Приведем пример одного из 8640 таких квадратов для шести уровней независимой переменной:

Группы испытуемых	Последовательности
	АБВГДЕ
	ВДГАЕБ
	ДВАЕБГ
	БГЕВАД
	ГЕБДВА
	ЕАДБГВ

Поскольку в латинском квадрате каждый уровень оказывается в каждой позиции последовательности, естественно, требуется столько групп испытуемых, сколько уровней независимой переменной. Если бы Готтсданкер и Уэй использовали (как это им и следовало сделать) латинский квадрат вместо реверсивного уравнивания, их испытуемые должны были разбиться на пять групп соответственно пяти уровням независимой переменной. Значит, в их опыте должны были бы принять участие пять или десять испытуемых вместо восьми, как это было на самом деле (ведь восемь на пять не делится).

Исследователи обычно вводят ограничение на латинский квадрат. Оно состоит в требовании, чтобы каждому уровню один раз непосредственно предшествовал каждый другой уровень. Такой квадрат называют сбалансированным квадратом. В приведенном выше латинском квадрате это условие не соблюдалось. Например, уровню Б только один раз предшествовали уровни А и Д, но три раза Е и ни разу В и Г. Метод получения сбалансированных квадратов приводится в работе Уагенаара (1969). Вот пример:

Группы испытуемых	Последовательности
	АБВГДЕ
	БГАЕВД
	ВАДБЕГ
	ГЕБДАВ
	ДВЕАГБ
	ЕДГВБА

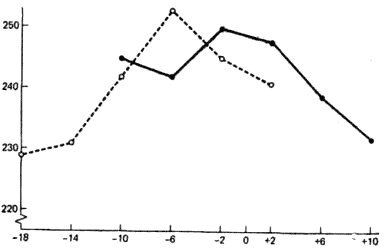
Если бы все эффекты переноса были связаны с непосредственно предшествующим уровнем, сбалансированный квадрат был бы очень эффективен. К сожалению, нет способа проверить, в действительности ли это так. Рассмотрим теперь систематические смешения (влияния последовательности), которые могут возникать даже при полном уравнивании.

Эффекты ряда

В многоуровневом эксперименте уровни независимой переменной образуют ряд — от наименьшего значения к наибольшему. При любой схеме уравнивания — интра- или кросс-индивидуальной — ответ на данный уровень независимой переменной может различаться в зависимости от того, какими были предшествующие ему уровни: более низкими, более высокими или смешанными.

Асимметричные эффекты. Об этих эффектах уже говорилось в главе 2 в связи с интраиндивидуальными схемами. Таково, например, влияние предшествующего опыта А на Б, но не наоборот. Эта идея может быть распространена на многоуровневые эксперименты с использованием кросс-индивидуального уравнивания. Предположим, имеется пять уровней независимой переменной и использована схема полного уравнивания (т. е. все 120 последовательностей). Поскольку каждому уровню один раз предшествовала каждая из возможных последовательностей остальных уровней, каждому уровню ни разу не предшествовали идентичные. В целом более низким уровням предшествовали более высокие уровни и наоборот. Например, самому низкому уровню не может предшествовать серия еще более низких уровней. Если имеется положительный перенос с меньших уровней на большие, но не наоборот, то больше всего от этого пострадает уровень А. Таким образом, асимметричный перенос в многоуровневом эксперименте будет благоприятно или неблагоприятно влиять на уровни в зависимости от степени их удаления от концов всего ряда уровней.

Эффект центрации. Другой эффект ряда был продемонстрирован в эксперименте Дж. Е. Кеннеди и Дж. Ландесмана (1963). Они провели два эксперимента, каждый по схеме латинского квадрата с двумя группами испытуемых. Задачей была токарная обработка деталей,

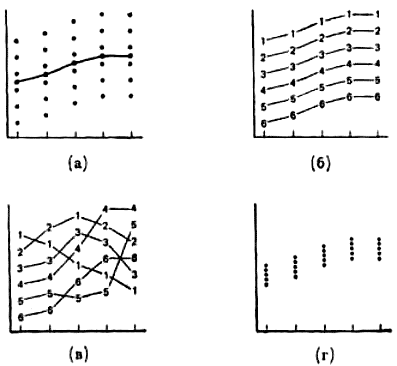
Рис. 7.7. Отношение между высотой рабочей поверхности и количеством обработанных деталей (Кеннеди и Ландесман, 1963). Ось абсцисс — высота рабочей поверхности (в дюймах, ниже (—) или выше (+) локтя). Ось ординат — среднее количество обработанных деталей. Пунктирная линия — условие А, сплошная — условие Б

независимой переменной являлась высота работ чей поверхности. Диапазон уровней в одном эксперименте пересекался с диапазоном уровней в другом. Независимой переменной служила высота рабочей поверхности. Зависимой переменной было среднее число деталей, обработанных в течение 3-минутной пробы.

На рис. 7.7 отдельно для каждой группы показаны средние количества обработанных деталей. Интересно, что испытуемые в условии А, где наименьший уровень равнялся 45 см, обнаружили наибольшую продуктивность при 15 см, в то время как испытуемые в условии Б работали на этом уровне относительно плохо. Эта вторая группа, для которой наименьшим был уровень 25 см, показала наилучшие результаты при уровне -5 и +5 см.

В этом эксперименте, таким образом, наиболее благоприятными оказались уровни, близкие к середине ряда, а не к его краям. Это были как раз, те единственные уровни, которым в последовательностях предшествовали как более низкие, так и более высокие уровни. Вы, конечно, можете сказать, что эти средние уровни казались для испытуемых «типичными» и поэтому наиболее удобными. Однако ваше объяснение имеет столько же оснований, сколько и мое. Ясно только одно: в этих опытах обнаружил себя эффект центрации.

Схемы полного позиционного уравнивания я латинского квадрата, в отличие от схемы реверсивного уравнивания, не требуют такого сильного допущения, как однородность переноса от одной позиции к следующей за ней. Однако в них сохраняется допущение, что отношение между настоящим и предшествующими уровнями не играет роли. Целый же ряд данных опровергает это (Поултон, 1973). Оказывается, важно, какие уровни в основном предшествуют: более низкие, более высокие или смешанные.

Как быть?

При использовании кросс-индивидуального уравнивания прежде всего стоит избегать реверсивного уравнивания. Поскольку полное уравнивание, как правило, оказывается 301непрактичным, стоит обращаться к схеме латинского квадрата, особенно сбалансированного квадрата. Далее, для избежания отрицательного переноса из-за утомления необходимо разнести пробы во времени. Хорошо также разделить эксперимент на две части и использовать два перекрывающихся ряда уровней независимой переменной. Если впоследствии эффектов ряда не обнаружится, это будет хорошим показателем того, что удалось избежать смешения из-за влияния последовательности. Как мы увидим в следующем параграфе, в многоуровневых экспериментах кросс-индивидуальное уравнивание, действительно, имеет одно важное преимущество перед межгрупповыми схемами. Этот подход слишком хорош, чтобы быть оставленным только потому, что он никогда не приводит к безупречному эксперименту. Каковы возможности этого подхода?

Представимость индивида

На рис. 7.8 (а) представлены вымышленные данные, демонстрирующие отношение между независимой и зависимой переменными в схеме межгрупповых сравнений.

Каждая маленькая точка соответствует одному испытуемому. Среднее по каждому уровню обозначено большой точкой, а полученная кривая есть линия, соединяющая средние. Теперь посмотрим, как выглядели бы эти данные в идеальном эксперименте, где испытуемый проверялся бы одновременно по всем уровням.

На рис. 7.8. (б) представлен один возможный вид этих результатов для нескольких испытуемых. Одной цифрой обозначены результаты одного и того же испытуемого

Рис. 7.8. Возможные соотношения усредненной кривой с данными идеального многоуровневого эксперимента, в котором каждому испытуемому одновременно предъявляются все уровни независимой переменной: (а) индивидуальные данные и усредненная кривая: (б) кривые по каждому испытуемому аналогичны усредненной кривой; (в) данные по каждому испытуемому дают различные кривые; (г) однородные группы испытуемых — высокая вероятность представительности усредненной кривой. Ось абсцисс — независимая переменная. Ось ординат — ответы испытуемых.

при различных уровнях независимой переменной. Линии, соединяющие ответы «одного испытуемого», по форме очень похожи на линию, соединяющую средние в (а). Конечно, возможен и другой вариант, когда линия, проходящая через средние, не обязательна так хорошо представляет все индивидуальные кривые, как это видно, например, на рис. 7.8 (в). Когда межгрупповой эксперимент дает результаты, представленные на рис. 7.8 (а), невозможно определить, какая из картин — (б) или (в) — имеет место в действительности. Из-за разброса индивидуальных данных в пределах одного уровня форма кривой оказывается неопределенной.

Существует два способа уменьшения этой трудности при использовании межгрупповой схемы: подбор сходных испытуемых и использование однородных групп. Если испытуемых провести через предварительные испытания, подобрать испытуемых по одинаковым уровням показанных результатов и затем предъявить так уравненным испытуемым различные уровни экспериментальной переменной, то вымышленные данные в виде наборов одинаковых цифр на рис. 7.8 (б) или (в) могут стать действительностью. Цифра 1 будет представлять одну уравненную группу испытуемых, 2 — другую группу и т. д. Тогда мы сможем непосредственно увидеть, какая картина верна — отражающая хорошее соответствие, как на (б), или довольно хаотическая, как на (в).

Второй способ основан на использовании одной, но очень однородной группы испытуемых, также может быть подобранной в предварительном эксперименте. Пример результатов такой группы приведен на рис. 7.8 (г). Теперь уже практически не имеет никакого значения, через какие точки пройдут индивидуальные линии: форма кривых будет примерно одной и той же. Оба описанных метода можно объединить, используя только одну однородную группу и распределяя испытуемых по различным уровням независимой переменной.

В этом пункте может несколько обеспокоить возможное пристрастие экспериментатора при отборе в испытуемые одних индивидов и отвержении других. Однако 304содержательных выводов о связи исследуемого поведения с уровнем экспериментальной переменной это ни в коей мере не коснется. Конечно, они будут относиться лишь к небольшой части популяции. Однако далее будет уже вопрос обобщения, который можно легко решить, исследуя другие гомогенные группы с более высокими и более низкими уровнями результатов.

Если же вместо всего сказанного будет использовано кросс-индивидуальное уравнивание с предъявлением каждой из пяти последовательностей нескольким испытуемым, то можно будет получить более ясную картину. Хотя кривую для каждой определенной последовательности нельзя будет «очистить» от зашумляющих влияний последовательности, эти влияния будут одинаковыми для всех испытуемых, которым будет предъявлена эта последовательность. Если, говоря в общем, все индивидуальные кривые для данной последовательности имеют одинаковую форму, это является хорошим свидетельством того, что вся групповая кривая по всем последовательностям действительно представляет индивидуальные данные. Поскольку одному и тому же испытуемому предъявляется каждый уровень независимой переменной (хотя и не одновременно), кросс-индивидуальная схема больше приближается к идеальному эксперименту — именно в этом отношении, — чем межгрупповая схема. Она имеет лучшую внутреннюю валидность по параметру представленности индивида.

Нет ли искажений?

Если бы вы проводили эксперимент с целью определить, как влияет вес дротика на точность его метания, вы хотели бы быть уверены, что в ваши измерения не вкрались ошибки. Если вы пользуетесь линейкой для измерения при каждом броске величины отклонения дротика от центра мишени, то, естественно, вам бы не хотелось, чтобы на вашей линейке расстояние между отметками 20 и 25 см было в три раза больше расстояния между 5 и 10 см. (Если бы это было так, вы скорее всего вернули бы линейку в магазин оборудования для фокусов.) Точно так же вы забраковали бы весы, стрелка которых едва отклоняется при помещении на них легкого дротика, но сразу же зашкаливает при чуть более тяжелом весе. Вы хорошо знаете, что использование подобных искажающих измерительных устройств приведет к тому, что кривая, отражающая отношение между независимой переменной (весом дротика) и зависимой переменной (величиной ошибки попадания в цель), будет весьма неточной. Вообще говоря, может быть вы и обнаружите, что метание становится более точным по мере увеличения веса. Но вы не сможете проверить гипотезу об «абсолютно-абсолютном» отношении (например, что происходит уменьшение ошибки на 5 см с увеличением веса на 1 унцию).

Конечно, вы не собираетесь делать подобных ошибок в своих экспериментах. Однако существует два вида измерений, в которых нужно приложить особые усилия для избежания искажений. Во-первых, это измерения очень маленьких физических величии. Примером может служить регистрация кожно-гальванической реакции — изменений сопротивления кожи «электрическому току, которые возникают, когда человек пугается или говорит неправду. Чтобы зарегистрировать реакцию, электрическое изменение должно быть усилено. Как мы можем быть уверены в том, что двойное увеличение амплитуды движения пера самописца означает двойное увеличение кожно-гальванической реакции? Обычно усилитель имеет максимальную чувствительность к определенной скорости нарастания или уменьшения тока. Если изменение нарастает либо быстрее, либо медленнее, оно уже не будет усиливаться в такой же пропорции. Итак, существуют такие области психологических исследований, где экспериментатор должен быть совершенно уверен в характеристиках измерительных приборов.

Проблемы искажения возникают и в тех случаях, когда используется психологическое шкалирование. Предположим, мы прошкалировали, как это было описано в одном из предшествующих разделов, шутки от «веселых» до «пустых», используя средние оценки-баллы, данные группой экспертов. Можем ли мы быть уверены о том, что различие в забавности между шутками, получившими оценку «2» и «4», такое же, как между шутками с оценкой «6» и «8»? Вероятно, нет. Следовательно, если бы мы проводили эксперимент для выяснения того, как влияет забавность шутки на ее запоминание, и проверяли бы какую-то точную гипотезу (например, что запоминаемость растет пропорционально росту забавности), мы не могли бы с уверенностью сказать, подтверждает форма кривой гипотезу или нет. Для правильного проведения такого эксперимента вы должны использовать более изощренные методы шкалирования, чем те, которые могут быть описаны в этой книге (см. Торгерсон, 1958). Сейчас же вы должны запомнить, что содержательная интерпретация формы кривых, полученных с помощью субъективного шкалирования переменных, всегда требует доказательства того, что переменные не были искажены.

В идеальном эксперименте, направленном на проверку гипотезы о некотором точном количественном отношении, не должно быть искажений при измерении независимой и зависимой переменных. Однако в реальном эксперименте всегда есть некоторое искажение. Если искажение настолько велико, что отношение, найденное в действительном эксперименте, не представляет отношения, которое могло бы быть найдено в идеальном эксперименте, то внутренняя валидность существенно ослаблена.

Ранее в этой главе было показано, что для проверки любой количественной гипотезы — неважно, сформулирована она в количественных терминах или нет — необходимо использовать достаточное число уровней независимой переменной. Слишком малое число уровней приводит к плохой представленности отношения между независимой и зависимой переменными. Внутренней валидности здесь угрожает не столько ненадежность или смешение, сколько неполнота независимой переменной. Было показано, что, во-первых, групповая кривая может не представлять индивидуальные и, во-вторых, что искаженные результаты измерения будут давать ложное отношение. В обоих случаях отношение между независимой и зависимой переменными оказывается невыявленным. Теперь мы знаем три пути, которые могут угрожать внутренней валидности, три причины того, что результаты реального эксперимента могут плохо представлять отношение между независимой и зависимой переменными, которое могло бы быть обнаружено в идеальном эксперименте: (1) ненадежность, (2) систематическое смешение и (3) неверно найденное отношение.

Краткое изложение

Было рассмотрено три возможных двухуровневых эксперимента, которые оказались совершенно неадекватными но сравнению с аналогичным реально проверенным многоуровневым экспериментом. На эт