
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задачи оптимизации на графах. Алгоритм Краскала построения минимального остовного дерева
Описание Алгоритм Краскала изначально помещает каждую вершину в своѐ дерево, а затем постепенно объединяет эти деревья, объединяя на каждой итерации два некоторых дерева некоторым ребром. Перед началом выполнения алгоритма, все рѐбра сортируются по весу (в порядке неубывания). Затем начинается процесс объединения: перебираются все рѐбра от первого до последнего (в порядке сортировки), и если у текущего ребра его концы принадлежат разным поддеревьям, то эти поддеревья объединяются, а ребро добавляется к ответу. По окончании перебора всех рѐбер все вершины окажутся принадлежащими одному поддереву, и ответ найден. Существует несколько алгоритмов для нахождения минимального остовного дерева. Некоторые наиболее известные из них: алгоритм Прима; алгоритм Краскала (или алгоритм Крускала); алгоритм Борувки.
(Пример минимального остовного дерева в графе.Числа на ребрах обозначают вес ребер.) Задача о нахождении минимального остовного дерева встречается в постановке: допустим, есть n городов, которые надо соединить дорогами, так, чтобы можно было добраться из любого города в любой другой (напрямую или через другие города). Разрешается строить дороги между заданными парами городов и известна стоимость строительства каждой дороги. Требуется решить, какие дороги нужно строить, чтобы минимизировать общую стоимость строительства.математического аппарата теории графов и системного подхода для отображения и алгоритмизации комплексов взаимосвязанных работ, действий или мероприятий для достижения четко поставленной цели. 20. Сетевое планирование: основная идея и модели решаемых задач Сетевое планирование – метод управления, основанный на использовании математического аппарата теории графов и системного подхода для отображения и алгоритмизации комплексов взаимосвязанных работ, действий или мероприятий для достижения четко поставленной цели. Основная цель сетевого планирования – сокращение до минимума продолжительности проекта. Задача сетевого планирования состоит в том, чтобы графически, наглядно и системно отобразить и оптимизировать последовательность и взаимозависимость работ, действий или мероприятий, обеспечивающих своевременное и планомерное достижение конечных целей. Для отображения и алгоритмизации тех или иных действий или ситуаций используются экономико-математические модели, которые принято называть сетевыми моделями, простейшие из них - сетевые графики. С помощью сетевой модели руководитель работ или операции имеет возможность системно и масштабно представлять весь ход работ или оперативных мероприятий, управлять процессом их осуществления, а также маневрировать ресурсами. Метод сетевого планирования и управления (СПУ) является методом решения задач исследования операций, в которых необходимо оптимально распределить сложные комплексы работ. Методы СПУ используются при планировании сложных комплексных проектов, например, таких как:− строительство и реконструкция каких-либо объектов;− выполнение научно-исследовательских и конструкторских работ;− подготовка производства к выпуску продукции;− перевооружение армии;− развертывание системы медицинских или профилактических мероприятий. Характерной особенностью таких проектов является то, что они состоят из ряда отдельных, элементарных работ. Они обуславливают друг друга так, что выполнение некоторых работ не может быть начато раньше, чем завершены некоторые другие. Например, укладка фундамента не может быть начата раньше, чем будут доставлены необходимые материалы; эти материалы не могут быть доставлены раньше, чем будут построены подъездные пути; любой этап строительства не может быть начат без составления соответствующей технической документации и т.д. СПУ состоит из трех основных этапов: 1)Структурное планирование. 2)Календарное планирование.3)Оперативное управление. Структурное планирование начинается с разбиения проекта на четко определенные операции, для которых определяется продолжительность. Затем строиться сетевой график выполнения работ. Календарное планирование предусматривает построение календарного графика, определяющего моменты начала и окончания каждой работы и другие временные характеристики сетевого графика. В ходе оперативного управления используются сетевой и календарных графики для составления периодических отчетов о ходе выполнения проекта. Здесь возможна корректировка проекта. Сущность метода сетевого планирования и управления (СПУ) заключается в особом моделировании исследуемого процесса, а именно – создаётся информационно-динамическая модель задачи. В качестве такой модели используется сетевой график, который изображается в виде ориентированного графа. Основными понятиями сетевой модели являются работа и события. Работа- это процесс приводящий к определенному результату и требующих затрат определенных ресурсов. События - момент времени когда завершаются другие и начинаются новые работы. Работа изображается на графики стрелкой и указывает на то что начало последующей операции зависит от результатов предыдущей. Использование методов сетевого планирования способствует сокращению сроков создания новых объектов на 15-20%, обеспечению рационального использования трудовых ресурсов и техники.
|
|||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 586; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.147.4 (0.004 с.) |
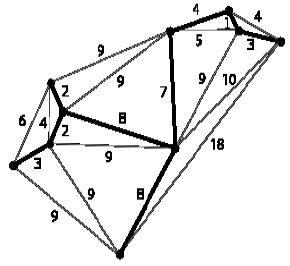 Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рѐбер.
Минимальное остовное дерево (или минимальное покрывающее дерево) в связанном, взвешенном, неориентированном графе — это остовное дерево этого графа, имеющее минимальный возможный вес, где под весом дерева понимается сумма весов входящих в него рѐбер.


