
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дослідження шумів аналого-цифрового перетворювачаСодержание книги
Поиск на нашем сайте Мета роботи: закріпити на практиці основні поняття, пов’язані з математичними моделями та стохастичними властивостями шумів квантування дискретних сигналів, зокрема, на виході аналого-цифрового перетворювача..
Короткі теоретичні відомості Реальні «первинні» сигнали як правило належать до класу аналогових, тобто неперервні як у часі, так і за своїми значеннями. В той же час цифрові системи обробки сигналів належать до класу дискретних систем. Тому для обробки «первинних» сигналів в цифрових система вони, по-перше, повинні бути дискретизовані у часі. Окрім того, зазначимо, що для зображення відліків дискретних сигналів, наприклад у двійковій системі числення, потрібно мати у загальному випадку необмежену кількість розрядів. В цифрових же системах обробки сигналів застосовуються елементи пам’яті (регістри, комірки пам’яті) та операційні пристрої (суматори, перемножувачі), які мають обмежену розрядність. Тому, по-друге, відліки дискретних сигналів підлягають ще і кватуванню, тобто наближеному їх зображенню з використанням обмеженої кількості розрядів. При цьому виникають похибки, які називають похибками квантування. По суті квантування, це нелінійне безінерційне перетворення сигналу, тобто
де В формулі (5.1)
Формулу (5.2) можна переписати так:
Рис. 5.1. Лінійна модель процесу квантування Відносно шуму квантування 1. 2. 3. Послідовність 4. Послідовність Оскільки дискретні відліки сигналів зображуються числами (у певній системі числення, як правило двійковій), то квантування сигналів по суті зводиться до наближеного зображення чисел обмеженою кількістю розрядів Квантування чисел виконується двома способами: округлювання чисел і зрізання чисел. У першому випадку число
де При квантуванні методом зрізування у
Дискретизація та квантування сигналів виконується в аналого-цифрових перетворювачах (АЦП). На вході АЦП діє аналоговий сигнал Література: [1, стор. 296 - 306].
Завдання до лабораторної роботи 1. Дослідити статистичні властивості шуму квантування (побудувати гістограму, знайти оцінки середнього, дисперсії, коефіцієнта кореляції) для АЦП, у якому квантування чисел здійснюється способом округлювання. 2. Дослідити статистичні властивості шуму квантування (побудувати гістограму, знайти оцінки середнього, дисперсії, коефіцієнта кореляції) для АЦП, у якому квантування чисел здійснюється способом зрізування.
Порядок виконання роботи Для виконання роботи необхідно запустити програмне середовище MATCAD та виконати наступні пункти роботи. 1. Отримати реалізацію випадкового дискретного процесу шляхом генерації рівномірно розподілених чисел за допомогою функції rand. Зобразити реалізацію графічно. 2. Обчислити оцінки математичного сподівання, дисперсії, коефіцієнта кореляції та побудувати гістограму отриманої в п. 1 реалізації. 3. За допомогою функції quantize на основі отриманої в п. 1 реалізації дискретного випадкового процесу побудувати реалізацію квантованої послідовності з використанням методу округлювання чисел. Зобразити отриману квантовану послідовність графічно. 4. На основі побудованої в п 3 реалізації квантованої послідовності з використанням методу округлювання чисел знайти оцінки математичного сподівання, дисперсії, коефіцієнта кореляції та побудувати гістограму. Отримані оцінки порівняти з оцінками в п. 2. 5. Порівняти дискретну послідовність, отриману в п. 1, з квантованою послідовністю із п. 3 на основі наступного критерію
де 6. За допомогою функції quantize на основі отриманої в п. 1 реалізації дискретного випадкового процесу побудувати реалізацію квантованої послідовності з використанням методу зрізування чисел. Зобразити отриману квантовану послідовність графічно та виконати дослідження, аналогічні пп. 4, 5. 7. Проаналізувати отримані результати за пп. 1 – 6 і зробити висновки. Контрольні питання 1. Чим визвана необхідність виконувати квантування відліків дискретного сигналу? 2. Що є причиною виникнення шумів квантування? 3. Що таке крок квантування і як він визначається? 4. Дайте означення нелінійної моделі процесу квантування. 5. Сформулюйте поняття лінійної моделі процесу квантування. 6. У чому полягає спосіб округлювання при квантуванні відліків дискретного сигналу? 7. У чому полягає спосіб зрізування при квантуванні відліків дискретного сигналу? 8. Яким розподілом описуються шуми квантування при використанні способу округлювання? 9. Яким розподілом описуються шуми квантування при використанні способу зрізування? 10. Від чого залежить величини дисперсія шуму квантування? 11. Запишіть вирази для математичних сподівань шумів квантування при використанні способу округлювання і способу зрізування чисел. Лабораторна робота 6
|
||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 142; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

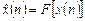 , (5.1)
, (5.1) -
-  -й відлік дискретного сигналу, який представлений
-й відлік дискретного сигналу, який представлений  -розрядним числом;
-розрядним числом; 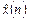 -
-  -розрядним числом
-розрядним числом  ;
;  - нелінійна функціональна залежність.
- нелінійна функціональна залежність. . (5.2)
. (5.2) і тоді похибку квантування
і тоді похибку квантування 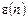 можна розглядати як адитивний дискретний випадковий процес, який називають шумом квантування. Такий підхід дає можливість розглядати лінійну модель процесу квантування (рис. 5.1) [1].
можна розглядати як адитивний дискретний випадковий процес, який називають шумом квантування. Такий підхід дає можливість розглядати лінійну модель процесу квантування (рис. 5.1) [1].
 (коли використовується двійкова система числення);
(коли використовується двійкова система числення); з нульовим математичним сподіванням
з нульовим математичним сподіванням  і дисперсією
і дисперсією ,
, - оператор математичного сподівання.
- оператор математичного сподівання.
 . Тоді для математичного сподівання шуму
. Тоді для математичного сподівання шуму 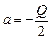 , а дисперсія
, а дисперсія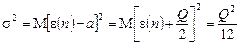 .
. . На виході маємо відгук
. На виході маємо відгук 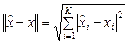 ,
,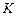 - кількість елементів (відліків) у послідовності.
- кількість елементів (відліків) у послідовності.


