Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Аналіз проходження дискретних випадкових сигналів через лдсСодержание книги
Поиск на нашем сайте
Мета роботи: ознайомитись на практиці з методами стохастичного аналізу стаціонарних ЛДС при дії на вході дискретних випадкових сигналів. Короткі теоретичні відомості Розглянемо деяку ЛДС (див. рис. 4.1), на вході якої діє дискретний випадковий процес
Рис. 4.1. Лінійна дискретна система
Формально для відгуку ЛДС можемо записати:
Введемо позначення для математичних сподівань:
Отже, згідно зі співвідношенням (4.2), математичне сподівання відгуку ЛДС у певний момент часу Зазначимо, що згідно з умовою фізичної можливості
Кореляційна функція відгуку ЛДС. Перейдемо тепер безпосередньо до розгляду кореляційної функції процесу на виході ЛДС. При цьому дисперсію зможемо знайти як частинний випадок кореляційної функції коли зсув між значеннями відгуку дорівнює нулеві. Оскільки при знаходженні кореляційної функції випадкового процесу використовується процедура центрування останнього, то спершу розглянемо представлення центрованого процесу на виході ЛДС. Центрований дискретний процес на виході ЛДС позначимо так:
де
отримаємо процес з нульовим математичним сподіванням. Тоді, враховуючи означення для кореляційної функції відгуку ЛДС, маємо
для стаціонарних ЛДС. Нагадаємо тепер, що коли для кореляційної функції
Взаємна кореляційна функція впливу і відгуку ЛДС. Знову розглянемо ЛДС (див. рис. 4.1). Використовуючи зображення центрованого відгуку системи
Оскільки перший співмножник в квадратних дужках у правій частині не залежить від індексу підсумовування, то його можна внести під знак суми і записати
Література: [1, стор. 279 - 286].
Завдання до лабораторної роботи 1. Виконати стохастичний аналіз нерекурсивної ЛДС при дії на вході дискретного випадкового сигналу (оцінити математичне сподівання, дисперсію, коефіцієнт кореляції та побудувати гістограму за реалізацією вихідного процесу). 2. Виконати стохастичний аналіз рекурсивної ЛДС при дії на вході дискретного випадкового сигналу (оцінити математичне сподівання, дисперсію, коефіцієнт кореляції та побудувати гістограму за реалізацією вихідного процесу).
Порядок виконання роботи Для виконання роботи необхідно запустити програмне середовище MATCAD та виконати наступні пункти роботи. 1. Здійснити стохастичний аналіз нерекурсивної ЛДС при дії процесу ковзного середнього. Для цього 1.1. Отриману в п. 2 лабораторної роботи 3 реалізацію процесу ковзного середнього пропустити через нерекурсивну ЛДС (коефіцієнти системи задаються викладачем) за допомогою функції filter і отримати реалізацію на виході. 1.2. Зобразити та порівняти реалізації процесів на вході і виході ЛДС. 1.3. За допомогою функцій mean, std і xcorr розрахувати оцінки математичного сподівання, дисперсії і коефіцієнта кореляції вихідного процесу. 1.4. За допомогою функції hist побудувати гістограму реалізації процесу на виході. 2. Здійснити стохастичний аналіз рекурсивної ЛДС при дії процесу ковзного середнього. Для цього дослідження, аналогічні пп. 1.1 – 1.4, виконати для рекурсивної системи. 3. Здійснити стохастичний аналіз нерекурсивної ЛДС при дії процесу авторегресії-ковзного середнього. Для цього слід скористатись реалізацією, сформованою в п. 5 лабораторної роботи 3 і далі виконати дослідження, аналогічні пп. 1.1 – 1.4, але для процесу авто регресії-ковзного середнього. 4. Здійснити стохастичний аналіз рекурсивної ЛДС при дії процесу авторегресії-ковзного середнього. Для цього слід скористатись реалізацією, сформованою в п. 5 лабораторної роботи 3 і далі виконати дослідження, аналогічні п. 2, але для процесу авто регресії-ковзного середнього. 5. Проаналізувати отримані результати за пп. 1 – 4 і зробити висновки. Контрольні питання 1. Що таке стохастичний аналіз ЛДС в рамках кореляційної теорії? 2. Запишіть формально зв’язок між вхідним і вихідним випадковими процесами для ЛДС у часовій області. 3. Наведіть співвідношення між математичними сподіваннями процесів на вході і виході ЛДС. 4. Що таке центрований випадковий процес? 5. Запишіть співвідношення для визначення кореляційної функції випадкового процесу на виході ЛДС. 6. Як знайти дисперсію випадкового процесу на виході ЛДС коли відома його кореляційна функція? 7. Наведіть означення взаємної кореляційної функції? 8. Чи можна визначити взаємну кореляційну функцію впливу і відгуку ЛДС коли відома автокореляційна функція випадкового процесу на вході?
Лабораторна робота 5
|
||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 92; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.145.41 (0.007 с.) |

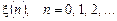 , де
, де  - нормований відносно інтервалу дискретизації час. Відомі розподіли ймовірностей вхідного процесу
- нормований відносно інтервалу дискретизації час. Відомі розподіли ймовірностей вхідного процесу 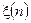 та імпульсна характеристика
та імпульсна характеристика
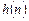 ЛДС. Потрібно знайти моментні функції (математичне сподівання, дисперсію, кореляційну функцію) процесу на виході
ЛДС. Потрібно знайти моментні функції (математичне сподівання, дисперсію, кореляційну функцію) процесу на виході  . Таке дослідження процесу на виході ЛДС називають стохастичним аналізом в рамках кореляційної теорії.
. Таке дослідження процесу на виході ЛДС називають стохастичним аналізом в рамках кореляційної теорії.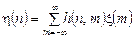 . (4.1)
. (4.1)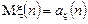 і
і  . Тоді можемо записати:
. Тоді можемо записати: (4.2)
(4.2) коли
коли  . Тому в (4.2) всі доданки з
. Тому в (4.2) всі доданки з 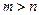 дорівнюють нулеві, тобто можна записати
дорівнюють нулеві, тобто можна записати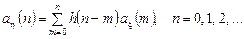 (4.3)
(4.3)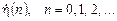 ,
, . Тепер, використовуючи співвідношення (4.1) і (4.2), можемо записати
. Тепер, використовуючи співвідношення (4.1) і (4.2), можемо записати =
=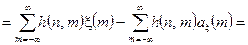


 , (4.4)
, (4.4)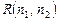 деякого дискретного процесу покласти
деякого дискретного процесу покласти  , то отримуємо дисперсію цього процесу
, то отримуємо дисперсію цього процесу  . Таким чином, використовуючи отриманий вище вираз (4.4) для кореляційної функції, можемо записати співвідношення для дисперсії відгуку ЛДС:
. Таким чином, використовуючи отриманий вище вираз (4.4) для кореляційної функції, можемо записати співвідношення для дисперсії відгуку ЛДС: ,
, 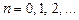
 , представленого правою частиною співвідношення (4.1), можемо записати для взаємної кореляційної функції вхідного процесу
, представленого правою частиною співвідношення (4.1), можемо записати для взаємної кореляційної функції вхідного процесу 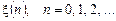 і процесу на виході ЛДС
і процесу на виході ЛДС 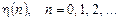 у такому вигляді:
у такому вигляді:
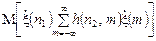 .
.

 ,
,