
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание диаграммы плавкостиСодержание книги
Поиск на нашем сайте Данную диаграмму плавкости можно рассматривать как две независимые диаграммы плавкости двух бинарных систем: В – АВ и АВ - А. Разбиваем диаграмму на 7 областей (рис.1). В области I система гомогенная. Однородный расплав, состоящий из веществ А и В В области II система гетерогенная. Кристаллы В и расплав А+В В области III – IV система гетерогенная. Кристаллы А2В и расплав А+В В областях V система гетерогенная. Кристаллы А и расплав А+В В области VI система гетерогенная. Кристаллы А и кристаллы А2В В области VII система гетерогенная. Кристаллы А2В и кристаллы В КРИВЫЕ ОХЛАЖДЕНИЯ По диаграмме кристаллизации строим кривые охлаждения (рис.3) Вариантности системы в точках, принадлежащих данным кривым, описываем по правилу фаз Гиббса. Правило фаз Гиббса. Если в гетерогенной системе давление и температура во всех фазах одинаковы, а число молей всех компонентов в каждой фазе постоянно, то такое ее состояние называется фазовым равновесием. Условием фазового равновесия является равенство химического потенциала компонента в одной фазе его значению в любой другой фазе. µkα = µkβ, (4.1) где µkФ = µk0,Ф(T,p) + RTlnN kФ γkФ. Чтобы охарактеризовать состояние гетерогенной системы, необходимо знать температуру, давление и концентрацию компонентов в каждой фазе. Но если в системе установилось фазовое равновесие, то только часть этих переменных являются независимыми, так как концентрации компонентов в отдельных фазах связаны уравнением (4.1). Число независимых переменных, необходимое для описания равновесного состояния гетерогенной системы, называется вариантностью или числом термодинамических степеней свободы системы. Вариантность системы (ω) определяет также число независимых переменных, которые можно произвольно (в некоторых пределах) изменять, не нарушая состояния в системе, то есть не изменяя числа и вида фаз в ней. Вариантность системы зависит от числа компонентов и определяется правилом фаз Гиббса ω = K – Ф +2 – R – L, (4.2) где К – число компонентов; Ф – число фаз; R – число химических реакций в системе; L – число дополнительных уравнений связи между концентрациями компонентов. В данной работе рассматривается система без химических реакций и без дополнительных уравнений связи, которая в тоже время исследуется при постоянном давлении. Поэтому уравнение Гиббса будет иметь вид: ω = K – Ф +1. (4.3) Расчет Используя данное уравнение, рассчитываем вариантность системы по кривым охлаждения (рис.3) и диаграмме плавкости (рис.1). Расчет дан рядом с (рис.3) т. 1:К=1,Ф=1, w=1-1+1=1 т. 1¢: К=1, Ф=2, w=1-2+1=0 т. 1¢¢: К=1, Ф=1, w=1-1+1=1 т. 2: К=2,Ф=1 w=2-1+1=2 т. 2¢: К=2,Ф=2 w=2-2+1=1 т.2¢¢: К=2,Ф=3, w=2-3+1=0 т.2¢¢¢: К=2,Ф=2, w=2-2+1=1 т. 3: К=2,Ф=1, w=2-1+1=2 т. 3¢: К=2,Ф=3, w=2-3+1=0 т. 3'': К=2,Ф=2, w=2-2+1=1 т.4: К=2,Ф=1, w=2-1+1=2 т. 4¢: К=2,Ф=3, w=2-3+1=0 т. 4¢¢: К=2,Ф=2, w=2-2+1=0 т. 5: К=2, Ф=1, w=2-1+1=2 т.5': К=2,Ф=2, w=2-2+1=1 т.5'¢: К=2,Ф=3, w=2-3+1=0 т.5'¢¢: К=2,Ф=2, w=2-2+1=1 ОПРЕДЕЛЕНИЕ МАССЫ КРИСТАЛЛОВ. Вывод правила рычага. Массу кристаллов, выделившихся из расплава при его охлаждении, можно определить, используя правило рычага. Вывод этого правила приводим для точки О. Для этого составляем уравнение материального баланса по компоненту В при постоянной температуре. m m = mраствора + mкристаллов (5.2) Подставив уравнение (5.2) в уравнение (5.1), получаем (mраствора + mкристаллов ) Решаем последнее уравнение относительно массы кристаллов: mраствора mкристаллов [ φB(K) - φB(O) ] = mраствора [ φB(O) - φB(L) ] (5.4) Из получившегося уравнения составляем пропорцию: Расчет. Для точки О: КО=20, OL=45, mраствора=2-mкр mкр=2LO/(LO+OK) mкр=1,38 кг Для точки О': К'О'=10 O'L'=17 mкр=2L’O’/(L’O’+O’K’) mкр=1,25 кг УРАВНЕНИЕ ШРЕДЕРА. Вывод уравнения. Рассмотрим равновесную систему, состоящую из двух фаз – жидкой и твердой. Пусть каждая фаза представляет реальный раствор. При фазовом равновесии Тж = Ттв = Т; рж = ртв = р; µk ж = µkтв. Химический потенциал компонента в каждой фазе зависит от температуры, давления и активности компонента µkж = µk 0,ж(T,p) + RTlnakж; (6.1) µkтв = µk 0,тв(T,p) + RTlnakтв; (6.2) Где µk 0,ж(T,p) и µk 0,тв(T,p) – химические потенциалы чистого компонента в жидком и твердом состояниях при заданных температуре и давлении; аkж и аkтв – активности компонентов в равновесных фазах. Учитывая (6.1) и (6.2), уравнение (4.1) можно преобразовать к виду
При постоянных температуре и давлении
Из (6.4) следует, что отношение активностей компонентов в равновесных фазах при постоянных температурах и давлении – закон фазового равновесия. Если при заданных температуре и давлении добавить в одну из фаз некоторое количество компонента k, то это вызовет его перераспределение между фазами таким образом, что отношение активностей компонентов при вновь установившемся равновесии сохранится прежним. При изменении температуры или давления система перейдет в другое равновесное состояние, в котором изменится отношение активностей компонента в равновесных фазах и произойдет смещение равновесия. Рассмотрим, как изменение температуры при постоянном давлении влияет на изменение состава равновесных фаз. Для этого выразим в уравнении (6.3) активности через мольные доли
Полученное уравнение продифференцируем по температуре
Согласно уравнению Гиббса-Гельмгольца
где
Использовав уравнение (6.7), получим
Последнее уравнение в дифференциальном виде описывает влияние температуры на состав равновесных фаз при изобарном смещении равновесия, при переходе из равновесного состояния при одной температуре в равновесное состояние при другой температуре. Твердые растворы образуют компоненты, близкие по химическим и физическим свойствам и имеющим одинаковый тип кристаллической решетки. Если компоненты в твердой фазе не растворимы друг в друге, то из жидкого раствора выделяются кристаллы чистого вещества. В этом случае имеет место равновесие: жидкий двухкомпонентный раствор и кристаллы одного из компонентов (Nkтв =1, γkтв =1), а уравнение принимает вид
Проинтегрируем это уравнение, допустив, что
Здесь
Последнее уравнение носит название уравнения Шредера, в котором Из уравнения Шредера следует, что в случае идеальных растворов растворимость компонентов возрастает с увеличением температуры. Применение. Уравнение Шредера может быть использовано для решения различных задач: 1. Если известна температура кристаллизации чистого компонента и температура кристаллизации расплава заданного состава, то из уравнения (6.11) можно рассчитать мольную теплоту плавления компонента k:
2. Если мольная теплота плавления компонента известна, уравнение (6.11) можно решить относительно
3. Расчет понижения температуры кристаллизации компонентов из расплавов разного состава – Запишем уравнение (6.11) для компонента А:
Из уравнения (6.14)
Для разбавленных растворов (Nkтв →1, γkтв →1),
В разбавленных растворах
Величина, стоящая в уравнениях (6.15) и (6.16) перед величинами, выражающими состав раствора. Называется криоскопической постоянной, которая зависит только от свойств компонента А.
Расчеты.
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 627; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.008 с.) |

 φB(O) = mраствора
φB(O) = mраствора 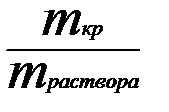 =
=  ;
; (5.5)
(5.5) (6.3)
(6.3) (6.4)
(6.4) (6.5)
(6.5) (6.6)
(6.6) (6.7)
(6.7) – изменение химического потенциала чистого компонента при переходе из твердого состояния в жидкое;
– изменение химического потенциала чистого компонента при переходе из твердого состояния в жидкое; – мольная теплота плавления компонента.
– мольная теплота плавления компонента. . (6.8)
. (6.8) (6.9)
(6.9) не зависит от температуры
не зависит от температуры
 (6.10)
(6.10)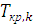 и
и 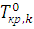 – температуры кристаллизации чистого компонента из раствора и температура кристаллизации чистого вещества. Уравнение (6.10) в интегральной форме описывает влияние температуры на равновесие «жидкий раствор – кристаллы компонента». Если жидкая фаза близка по свойствам к идеальному раствору (γkж =1), то уравнение (6.10) записывается в виде
– температуры кристаллизации чистого компонента из раствора и температура кристаллизации чистого вещества. Уравнение (6.10) в интегральной форме описывает влияние температуры на равновесие «жидкий раствор – кристаллы компонента». Если жидкая фаза близка по свойствам к идеальному раствору (γkж =1), то уравнение (6.10) записывается в виде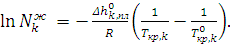 (6.11)
(6.11) – мольная доля компонента в жидком растворе, находящемся в уравнении с его кристаллами, то есть концентрация компонента в насыщенном растворе или растворимость компонента k при температуре
– мольная доля компонента в жидком растворе, находящемся в уравнении с его кристаллами, то есть концентрация компонента в насыщенном растворе или растворимость компонента k при температуре 
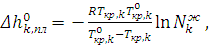 (6.12)
(6.12)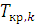 температуры, при которой из расплава начинают выделяться кристаллы компонента k:
температуры, при которой из расплава начинают выделяться кристаллы компонента k: (6.13)
(6.13) :
: (6.14)
(6.14) (6.15)
(6.15)

 (6.15)
(6.15) , поэтому последнее уравнение можно записать, используя d-шкалу
, поэтому последнее уравнение можно записать, используя d-шкалу (6.16)
(6.16)





