
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Двухфазное короткое замыканиеСодержание книги Поиск на нашем сайте
При двухфазном к.з. токи нулевой последовательности отсутствуют и поэтому для его анализа достаточно иметь только две схемы замещения: прямой и обратной последовательностей. Предположим, что эти схемы замещения уже составлены, приведены к простейшему виду и известны их результирующие
Для дальнейших рассуждений воспользуемся схемой рис. 4.10. Рис.4.9. Рис.4.10. Уравнения (4.8)-(4.9) дают лишь две связи между четырьмя неизвестными, поэтому для их решения нужны еще два уравнения, которые получают из граничных условий для двухфазного к.з.:
Система уравнений составлена для фазы При записи граничных условий для всех видов несимметрии принимают, что фаза За положительное направление фазных токов и их симметричных составляющих принимают направление к месту короткого замыкания. В дальнейшем условимся при записи симметричных составляющих фазы Согласно системе уравнений (4.2) следовательно, Согласно (4.3)-(4.5)
Используя (4.17)-(4.19), можно записать:
Согласно (4.2) токи в фазах будут:
Симметричные составляющие напряжения для фазы
Тогда в соответствии с (4.2) напряжения фаз будут:
Заметим, что напряжение неповрежденной фазы в два раза больше по модулю напряжения поврежденных фаз и противоположно по знаку.
Рис.4.11. а – векторная диаграмма токов; б – векторная диаграмма напряжений; в – комплексная cхема замещения Комплексная схема замещения предназначена для расчетов несиметричных режимов на расчетных столах переменного и постоянного тока. Конфигурация комплексной схемы замещения определяется по выражению для тока прямой последовательности для рассматриваемого вида несимметрии. Условные обозначения на комплексной схеме замещения:
По измерениям, проводимым на комлексной схеме замещения, набранной на расчетном столе постоянного тока, можно определить модули токов и напряжений всех последовательностей для фазы Зная из анализа каждого вида несимметрии положение векторов токов и напряжений всех последовательностей для фазы Так, для рассматриваемого вида несимметричного к.з. достаточно применить в комлексной схеме замещения только два измерительных прибора: амперметр, включаемый в разрыв последовательной цепи и вольтметр, подключаемый к точкам При этом, первый прибор покажет значение модуля тока прямой последовательности фазы Таким образом, ценность применения комплексных схем замещения состоит в простоте определения искомых фазных величин в любой точке длясети любой сложности, схемы замещения соответствующих последовательностей которой набраны и соединены между собой соответствующим образом на расчетном столе.
4.6.2. Однофазное короткое замыкание на землю
Для этого вида к.з. (см. рис.4.12) нужно иметь три схемы замещения – прямой обратной и нулевой последовательностей.
Для этого случая к.з. с учетом граничных условий можно записать следующие уравнения Рис.4.12.
  (4.23) Согласно (4.3)-(4.5) и (4.23) имеем: (4.23) Согласно (4.3)-(4.5) и (4.23) имеем:
Следовательно, Согласно (4.2) и (4.23) имеем: Таким образом, Токи в фазах согласно (4.23)-(4.24) будут:
Ток в земле будет равен:
Напряжения фаз
На рис. 4.13 представлены векторные диаграммы токов, напряжений и комплексная схема замещения при однофазном коротком замыкании на землю в точке Векторная диаграмма токов строится на основании формулы (4.24), а напряжений – исходя из того, что Угол
Рис.4.13. а - векторная диаграмма токов; б – векторная диаграмма напряжений;
в – комплексная схема замещения
4.6.3. Двухфазное короткое замыкание на землю
Для этого вида к.з. (см. рис.4.14) нужно иметь три схемы замещения – прямой обратной и нулевой последовательностей. Будем по прежнему считать, что эти схемы замещения приведены к простейшему виду и нам известны
Рис.4.14. Из (4.29) следует, что:
Так как то Подставляя выражение для Токи в фазах при двухфазном к.з.на землю будут:
Ток в земле при двухфазном к.з. на землю
Напряжения фаз
На рис. 4.15 представлены векторные диаграммы токов, напряжений и комплексная схема замещения при двухфазном коротком замыкании на землю в точке К.
Рис.4.15. а – векторная диаграмма токов; б – векторнафя диаграмма напряжений; в – комплексная схема замещения
4.10. Анализ однократной продольной несимметрии 4.10.1. Общие замечания
Продольную несимметрию в какой -либо точке трехфазной сети в общем виде можно представить включением в рассечку каждой фазы неодинако- вых сопротивлений. Такой подход универсален, так как позволяет получить расчетные выражения в самом общем виде. Однако указанный прием связан с необходимостью проведения сложных выкладок, а сам конечный результат характеризуется громоздкими выраже- ниями. Значительно проще и нагляднее проводить решение для каждого вида про- дольной несимметрии, используя характеризующие его граничные условия. В данном параграфе будут рассмотрены два вида наиболее часто встречающейся продольной несимметрии, а именно: разрыв одной фазы и разрыв двух фаз (в одном и том же месте). Основные уравнения падений напряжения в схемах замещения каждой последовательности, составленные для симметричной части сети, аналогичны уравнениям (4.3)-(4.5), и при чисто индуктивной цепи их можно представить в виде:
где
вующих последовательностей относительно места продольной несиммет- рии. Дополнительные связи между симметричными составляющими токов и напряжений устанавливаются из граничных условий рассматриваемой продольной несимметрии.
4.10.2. Разрыв одной фазы
Разрыв одной фазы (рис.4.17) можно характеризовать следующми граничными условиями:
Эти условия аналогичны граничным условиям двухфазного к.з. на землю, следовательно данная аналогия должна быть и в расчетных выражениях.
щие условия (4.58)-(4.59) приводят к равенствам:
Используя (4.55)-(4.56) и (4.60), выразим Рис.4.17.
В соответствии с (4.57) можно записать
откуда где верхний индекс (1) и далее (2) одновременно с нижним индексом После подстановки (4.63) в (4.54), получим:
Подставляя (4.63) в (4.61)-(4.62), найдем:
Для определения напряжений с одной из сторон продольной несииметрии (при разрыве одной фазы) нужно предварительно найти по схемам отдель- ных последовательностей симметричной части цепи соответствующие со-
ставляющие этих напряжений. Прибавив к ним Далее, зная все симметричные составляющие токов и напряжений, определяют фазные величины токов и напряжений путем сложения симметричных составляющих соответствующих фаз. В частности, для определения фазных токов в месте обрыва одной фазы могут быть использованы выражения, аналогичные (4.32), в которых ток Аналогично, для нахождения модуля фазных токов при обрыве одной фазы может быть использован коэффициент, определяемый по выражению, аналогичному (4.33).
На рис. 4.18 в качестве иллюстрации приведены векторные диаграммы напряжений по концам разрыва (соответственно в точках  и и  ), а на рис.4.19 – комплексная схема замещения. ), а на рис.4.19 – комплексная схема замещения.
Рис.4.18. Рис.4.19. 4.10.3. Разрыв двух фаз
При разрыве двух фаз (рис.4.20) граничные условия, очевидно будут:
то есть они аналогичны граничным условиям однофазного к.з.В соответствии с (4.23)-(4.24) следует, что симметричные составляющие тока фазы Рис.4.20.
достаточно сложить правые части уравнений (4.54)-(4.55) и сумму приравнять нулю. Далее, учитывая (4.70), получим:
где Для фазного тока целой фазы (фаза
Симметричные составляющие разности фазных напряжений в месте обрыва двух фаз определяются для обратной последовательности соответственно по (4.55) и (4.56), а для прямой последовательности проще по (4.71):
5.3. Методика расчета токов к.з. в установках напряжением до 1000 В Электрические установки напряжением до 1000 В, питаемые от распределительной сети электрической системы через понижающие трансформаторы, характеризуются, как правило, большой электрической удаленностью относительно источников питания. Это позволяет считать, что при к.з. за таким понижающим трансформатором напряжение в точке сети, где он присоединен, практически остается неизменным и равным своему номинальному значению. Достоверность расчета токов к.з. в установках напряжением до 1000 В зависит в основном от того, насколько правильно оценены и полно учтены все сопротивления короткозамкнутой цепи. Наряду с индуктивными сопротивлениями в рассматриваемой ситуации весьма существенную роль играют активные сопротивления таких элементов, как сборные шины и присоединения к ним, тансформаторы тока, контактные сопротивления выключателей, разъединителей, болтовых соединений шин, зажимов и разъемных контактов аппаратов, а также контакта непосредственно в месте к.з. и др., которыми при выполненни аналогичных расчетов для установок высокого напряжения всегда пренебрегают.
Точная оценка сопротивлений контактных соединений представляет трудную задачу, так как эти сопротивления зависят от многих трудноучитываемых факторов(состояния контактных поверхностей, степени затяжки болтов и др.). С другой стороны, отказ от учета этих сопротивлений приводит к излишнему преувеличению токов к.з. со всеми вытекающими отсюда последствиями, а именно, к применению более мощной аппаратуры и проводников большего сечения, то есть к неоправданным дополнительным затратам на электрооборудование. В принятых в 1966 г. Указаниях по проектированию силового электрооборудования промышленных предприятий рекомендуется при отсутствиидостоверных данных о переходных сопротивлениях учитывать их совокуп- но (включая и контакт в месте к.з.), вводя в короткозамкнутую цепь активное сопротивление, величина которого зависимости от места к.з. оценивается в пределах Нижний предел соответствует к.з. около распределительного щита подстанции, а верхний – при к.з. непосредствено у электроприемников, получающих питание от вторичных распределительных пунктов. Сопротивления понижающих трансформаторов до 1000 кВА, кабелей до 1000 В, магистральных и распределительных шинопроводов (со спаренными фазами), а также приближенные величины сопротивлений аппаратов напряжений до 1000 В приведены в справочниках. Сопротивления прямой последовательности шин (обычного исполнения) можно найти в справочниках или определить по выражению
где при этом следует принимать: для круглых шин (радиусом Для пакета из нескольких полос под Сопротивлеие нулевой последовательности шин зависит от многих факторов (расположения и выполнения заземляющей проводки, близости металлоконструкций и т.д.) и изменяется в широких пределах. Ориентировочно можно считать, что составляющие этого сопротивления находятся в пределах: При составлении схемы замещения следует руководствоваться указаниями § 2.2. Поскольку сопротивления большинства элементов рассматриваемых установок задаются в именованных единицах, то весь расчет обычно ведут также в именованных единицах; при этом ввиду малых значений самих сопротивлений их выражают в миллиомах ( Индуктивные сопротивления прямой последовательности воздушных и кабельных линий можно приближенно определить, принимая: =80 мОм – для кабельных линий. Активное сопротивление воздушных и кабельных линий можно рассчитать по формуле, если известны материал и сечение провода (жилы) фазы:
где Относительное активное сопротивление трансфрматора определяют как:
где ре, кВт; Относительное индуктивное сопротивление трансформатора можно определить по формуле:
где Сопротивления трансформатора в именованных единицах:
В качестве средних номинальных напряжений
|
|||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 2131; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.67.189 (0.012 с.) |

 и
и  , а также
, а также  .
.
 (4.17)
(4.17) , но она имеет силу для любой другой фазы.
, но она имеет силу для любой другой фазы. , но из (4.17)
, но из (4.17) 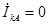 ,
, . (4.18)
. (4.18) (4.19)
(4.19)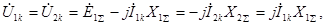
 (4.20)
(4.20)
 (4.21)
(4.21)
 (4.22)
(4.22)
 и т.д. служат для фиксации начала (
и т.д. служат для фиксации начала ( ) и конца набранной на расчетном столе схемы замещения соответствующей последовательности.
) и конца набранной на расчетном столе схемы замещения соответствующей последовательности. и
и  .
. Будем по прежнему считать, что эти схемы замещения приведены к простейшему виду и нам известны
Будем по прежнему считать, что эти схемы замещения приведены к простейшему виду и нам известны  .
.

 (4.24)
(4.24) , а используя (4.24), получим:
, а используя (4.24), получим:  .
. . (4.25)
. (4.25) (4.26)
(4.26)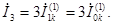 (4.27)
(4.27) (4.28)
(4.28) .
.

 между векторами
между векторами  и
и 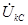 изменяется от 60 до
изменяется от 60 до  .
.
 Для этого вида к.з. уравнения связи с учетом граничных условий запишутся в следующем виде:
Для этого вида к.з. уравнения связи с учетом граничных условий запишутся в следующем виде:  (4.29) Согласно (4.3)-(4.5) и (4.29) имеем:
(4.29) Согласно (4.3)-(4.5) и (4.29) имеем: . (4.30)
. (4.30) ;
; 
 .
. ,
,
 из последнего выражения в (4.29), получим
из последнего выражения в (4.29), получим  ;
; 
 (4.31)
(4.31) . (4.32)
. (4.32) . (4.33)
. (4.33)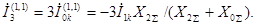 (4.34)
(4.34) (4.35)
(4.35)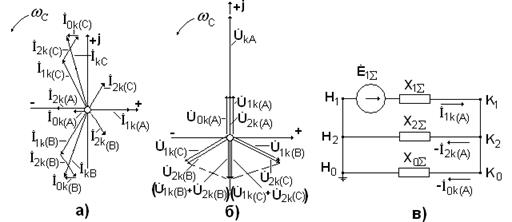
 (4.54)
(4.54)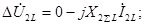 (4.55)
(4.55) (4.56)
(4.56) - симметричные составляющие падения напряжения фазы
- симметричные составляющие падения напряжения фазы  - результирующие реактивности схем замещения соответст-
- результирующие реактивности схем замещения соответст- (4.57)
(4.57)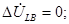 (4.58)
(4.58) (4.59)
(4.59) Так при разложении на симметричные составляю-
Так при разложении на симметричные составляю- (4.60)
(4.60) и
и  через
через  :
: (4.61)
(4.61) (4.62)
(4.62) ,
, , (4.63)
, (4.63)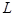 указывает обрыв соответственно одной и двух фаз.
указывает обрыв соответственно одной и двух фаз. . (4.64)
. (4.64) ; (4.65)
; (4.65) . (4.66)
. (4.66) получают симметричные составляющие напряжений с другой стороны продольной несимметрии.
получают симметричные составляющие напряжений с другой стороны продольной несимметрии. и реактивности
и реактивности  и
и 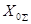 должны быть соответственно замененены током
должны быть соответственно замененены током  и реактивностями
и реактивностями  и
и  .
.
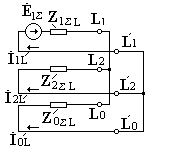
 (4.67)
(4.67)
 (4.68)
(4.68) (4.69)
(4.69) . (4.70) С другой стороны, поскольку согласно (4.69)
. (4.70) С другой стороны, поскольку согласно (4.69) (4.71)
(4.71) , (4.72)
, (4.72) (4.73)
(4.73) (4.74)
(4.74) (4.75)
(4.75) Ом.
Ом.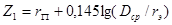 , (5.6)
, (5.6)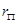 - активное сопротивление фазы;
- активное сопротивление фазы;  - среднее геометрическое расстояние между шинами фаз
- среднее геометрическое расстояние между шинами фаз  ;
;  - эквивалентный радиус шины;
- эквивалентный радиус шины; )
)  ; для полосовой прямоугольной шины (с размерами
; для полосовой прямоугольной шины (с размерами  и
и  )
)  .
. .
. ).
). Ом/км
Ом/км  мОм – для воздушных линий;
мОм – для воздушных линий;  Ом/км=
Ом/км= , (5.7)
, (5.7) - длина линии, км;
- длина линии, км;  - сечение провода(жилы) фазы,
- сечение провода(жилы) фазы,  ;
;  - удельная проводимость проводника,
- удельная проводимость проводника,  .
. , (5.8)
, (5.8) -активные потери мощности короткого замыкания в трансформато-
-активные потери мощности короткого замыкания в трансформато- - номинальная мощность трансформатора, кВА.
- номинальная мощность трансформатора, кВА. , (5.9)
, (5.9) -напряжение короткого замыкания трансформатора, %.
-напряжение короткого замыкания трансформатора, %.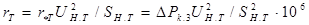 , мОм; (5.10)
, мОм; (5.10) мОм. (5.11)
мОм. (5.11) для соответствующих ступеней трансформации рекомендуется принимать: 690, 400, 230 В.
для соответствующих ступеней трансформации рекомендуется принимать: 690, 400, 230 В.


