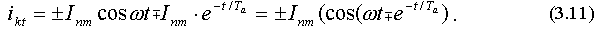Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы приведения схем замещения к простейшему видуСодержание книги
Поиск на нашем сайте
а)Замена нескольких генераторных ветвей, сходящихся в одной точке, одной эквивалентной.
Рис.2.4. Согласно [1] эквивалентная э.д.с., то есть э.д.с. генератора, которая заменяет э.д.с.
где б)Преобразование многолучевой звезды в соответствующий многоугольник
Рис.2.5. Сопротивления сторон многоугольника определяют по формуле
где
Далее, получив многоугольник, рассекают точку  и получают схему (рис.2.6), дальнейшее преобразование которой не вызывает затруднений. и получают схему (рис.2.6), дальнейшее преобразование которой не вызывает затруднений.
Рис.2.6. в)Преобразование трехлучевой звезды в треугольник и наоборот (рис.2.7)
Рис.2.7. В качестве примера приведем формулы для определения
г) Металлическое трехфазное к.з. находится в узле с несколькими сходящимися в нем ветвями (рис.2.8, а).
В этом случае этот узел можно разрезать, сохранив на конце каждой образовавшейся ветви такое же к.з. Далее полученную схему нетрудно преобразовать относительно любой из точек к.з., учитывая другие ветви с к.з., как нагрузочные с э.д.с, равными нулю (рис.2.8, б). Рис.2.8.
Рис.2.9.
д)Разнесение мощностей или токов, подходящих к вершине треугольника сопротивлений (рис.2.11, а, б) по ветвям разомкнутого треугольника (рис.2.11, в) При разнесении мощности расчетные соотношения имеют вид:
 ; ;  ; ; 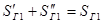 . (2.22) . (2.22)
Рис.2.11. a-исходная принципиальная схема;б-схема замещения;
Анализ трёхфазного к.з. Простейшая трёхфазная цепь - это цепь с сосредоточенными активными сопротивлениями и индуктивностями, при отсутствии в ней трансформаторных связей. Питание данной цепи осуществляется от источника с сопротивлением отличным от 0 и напряжение имеет незначительную амплитуду и постоянную частоту.
Рассмотрим схему замещения (рис.3.1.) Как видно, она является симмеричной, так как сопротивления всех трех фаз равны между собой. Рис.3.1. Предположим, что до к.з. в схеме протекал процесс, характеризуемый параметрами
Допустим, что произошло металлическое трехфазное к.з. так, что схема распалась на две независимые части.
После этого в левой части схемы наступит новый установившийся режим, характеризуемый параметрами: установившиеся значения токов фаз. Построим векторную диаграмму, характеризующую режим левой части схемы до к.з. и после к.з. (рис.3.2), где ось
Рис.3.2. Следует отметить, что в новом режиме фаза и величина токов изменились в сторону увеличения. Увеличение фазы (углового сдвига тока относительно напряжения своей фазы) обусловлено увеличением доли реактивной составляющей сопротивления цепи к.з. по сравнению с ее активной составляющей (сказывается отсутствие сопротивления нагрузок, имеющего преимущественно активную составляющую сопротивления с целью получения высокого значения коэффициента мощности). Аналитическое описание переходного процесса 3-х фазного к.з. в простейшей эл.цепи при питании ее от источника неограниченной мощности. дифференциальное уравнение равновесия падений напряжений для фазы
где Имея в виду, что в трехфазной сети с изолированной нейтралью в любой момент времени имеет место соотношение
где Решение (3.2), например, для фазы
где
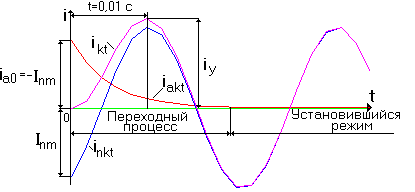
Первый член правой части (3.3) - периодическая составляющая
Рис.3.3.
Рис.3.5.
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 481; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.80.194 (0.007 с.) |


 генераторов и эквивалентное сопротивление, могут быть определены по формулам:
генераторов и эквивалентное сопротивление, могут быть определены по формулам: ; (2.17)
; (2.17)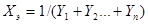 , (2.18)
, (2.18) - проводимости генераторных ветвей.
- проводимости генераторных ветвей.
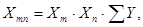 (2.19)
(2.19)
 - сопротивление стороны многоугольника
- сопротивление стороны многоугольника  ;
; -сопротивления лучей звезды
-сопротивления лучей звезды  и
и  -сумма проводимостей всех лучей звезды.
-сумма проводимостей всех лучей звезды.

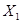 и
и 
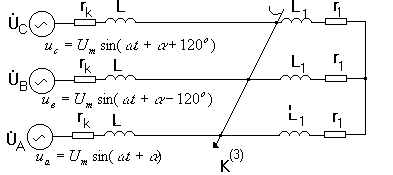
 ; (2.20)
; (2.20) . (2.21)
. (2.21)


 .
.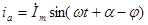 .
. , где
, где 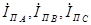 -
-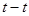 - есть ось времени.
- есть ось времени.
 , имеет вид
, имеет вид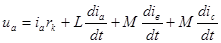 , (3.1)
, (3.1)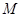 -коэффициент взаимоиндукции между фазами.
-коэффициент взаимоиндукции между фазами. , можно это уравнение представить (опуская индекс фазы)
, можно это уравнение представить (опуская индекс фазы) , (3.2)
, (3.2) - результирующая индуктивность фазы, то есть индуктивность с учетом влияния двух других фаз.
- результирующая индуктивность фазы, то есть индуктивность с учетом влияния двух других фаз. , (3.3)
, (3.3) - полное сопротивление присоединенного к источнику участка цепи или цепи к.з.;
- полное сопротивление присоединенного к источнику участка цепи или цепи к.з.; 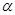 - угол, определяющий значение проекции
- угол, определяющий значение проекции 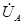 на ось времени
на ось времени  (иначе, фаза включения);
(иначе, фаза включения); - угол сдвига тока фазы по отношению к напряжению фазы в цепи к.з.;
- угол сдвига тока фазы по отношению к напряжению фазы в цепи к.з.; - постоянная времени цепи к.з.
- постоянная времени цепи к.з. . Второй член решения - апериодическая составляющая
. Второй член решения - апериодическая составляющая  . (3.4)
. (3.4)