
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По правилам дифференцирования дроби получим
б)
Решение. По правилам дифференцирования произведения получим
в)
Решение. Дифференцируем как сложную функцию.
г)
Решение.
Задача 6. С помощью правила Лопиталя вычислить пределы функций: 1) Решение. Непосредственная подстановка х = 0 приводит к неопределенности вида
2)
Решение. При
Задача 7. Исследовать функцию Решение.
Исследование выполним по примерной схеме, имеющейся в учебниках и практических руководствах. График можно строить либо по ходу исследования, либо конце исследования (рис.2).
Вертикальная асимптота может быть в точке разрыва или на границе области определения. Здесь вертикальная асимптота Здесь Итак,
5) Найти интервалы монотонности (возрастания и убывания) функции и точки экстремума. Найдем производную первого порядка.
Найдем критические точки первого рода и выясним знаки
Возьмем интервал
Итак, функция возрастает на интервалах
6) Найти интервалы выпуклости и вогнутости графика функции и точки перегиба. Вычислим производную второго порядка и найдем критические точки второго рода.
Задача 8. Три пункта А.В. и С расположены так, что угол АВС (рис.3) равен 600. Расстояние между пунктами А и В равно 200 км. Одновременно из пункта А выходит автомобиль, а из пункта В – поезд. Автомобиль движется по направлению к пункту В со стороны 80 км/ч, а поезд движется по направлению к пункту С со скоростью 50 км/ч. Через скорость времени расстояние между автомобилем и поездом будет наименьшим? Решение.
рис. 3.
Тогда получим уравнение
Отсюда
Квадратный трехчлен под корнем в знаменателе в ноль не обращается ни при каких действительных значениях t, поскольку его дискриминант Д Легко видеть, что при переходе через критическую точку t0 от меньших значений t к большим, например, от t = 1 до t = 2, первая производная меняет знак с минуса на плюс
Задача 9. Найти частные производные и полный дифференциал функции двух независимых переменных: а) Решение. Найти частные производные
Получим б) Решение. Найдем частные производные
Составим полный дифференциал
Задача 10. Найти экстремум функции Решение. Найдем частные производные: и смешанную производную Необходимое условие экстремума: Решим систему уравнений x = -9 Итак, точка P(-9; -3) критическая точка. Составим выражение а если Если Установим характер экстремума в точке P(-9; -3).
Задача 11. Найти неопределенные интегралы а) в) Предлагаемые интегралы можно, применив основные методы интегрирования; метод замены переменной подстановка, метод интегрирования по частям. Решение. а) Подстановка: или б) В первом из интегралов, стоящих справа, введем подстановку Второй интеграл справа является табличным Итак, в) Подстановка: Получим табличный интеграл типа г) Примем В первом из этих двух равенств обе части дифференцируем, чтобы найти Применив формулу интегрирования по частям, получим
д)
Такое равенство отношений с одинаковыми знаменателями возможны только в случае равенства числителей, то есть Приравнивая коэффициенты при x в одинаковых степенях в левой и правой частях последнего равенства, получим систему уравнений
Переходим к интегрированию !! Приведем две задачи геометрического характера, связанные с вычислениями определенного интеграла.
Задача 12. Вычислить площадь фигуры, ограниченной линиями
рис. 4.
Определенные интегралы вычисляются по ф>рмуле Ньютона-Лейбница
Задача 13. Вычислить объем тела, полученного в результате вращения
вокруг оси
рис. 5.
Задача 14. Найти частное решение дифференциального уравнения
Решение. Это уравнение первого порядка является линейным, так как это удовлетворяет общему виду линейных уравнений
или Приравняем нулю выражение, стоящее в скобках и получим уравнение с разделяющимися переменными А так как решение ищется в виде Задача 15. Найти область сходимости степенного ряда Решение. Область сходимости называется множество всех точек сходимости данного ряда. Найдем радиус и интервал сходимости.
Где 1) Подставим в данный степенной ряд 2) Подставляя в степенной ряд Итак, область сходимости данного степенного ряда
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 269; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.23.123 (0.062 с.) |
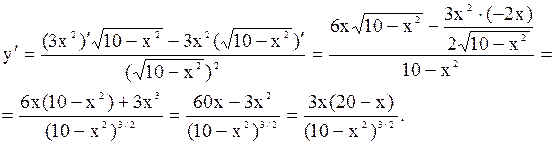
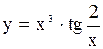 .
.


 . Это неявная функция.
. Это неявная функция.
 ,
,  ,
,  .
. .
. , следовательно, можно применить правило Лопиталя: заменить предел отношения функций пределом отношения их производных.
, следовательно, можно применить правило Лопиталя: заменить предел отношения функций пределом отношения их производных.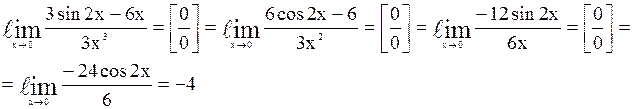

 получим неопределенность вида
получим неопределенность вида  , когда можно применить правило Лопиталя.
, когда можно применить правило Лопиталя.

 и построить ее график.
и построить ее график.





 Область определения функции
Область определения функции
 .
2) Найдем точки пересечения графика функции с осями координат. Пусть
.
2) Найдем точки пересечения графика функции с осями координат. Пусть  , тогда
, тогда  . Пусть
. Пусть  или
или  . Значит, график функции проходит через начало координат.
3) Проверить является ли функция четной, нечетной, общего вида.
. Значит, график функции проходит через начало координат.
3) Проверить является ли функция четной, нечетной, общего вида.
 .
Функция общего вида.
4) Найти асимптоты графика функции (вертикальные, наклонные, горизонтальные).
.
Функция общего вида.
4) Найти асимптоты графика функции (вертикальные, наклонные, горизонтальные).


 .
.  , - предел слева в точке
, - предел слева в точке  - предел справа. Наклонные асимптоты вида
- предел справа. Наклонные асимптоты вида  Найдем, если существуют конечные пределы
Найдем, если существуют конечные пределы 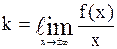 и
и  .
.
 - уравнение наклонной асимптоты.
- уравнение наклонной асимптоты.
 на полученных интервалах в окрестности критических точек. Критические точки: х1 = 0, х2 = 3, х3 = 1 - последняя н входит в область определения функции. Используя достаточные признаки экстремума, выясним, как меняет знак
на полученных интервалах в окрестности критических точек. Критические точки: х1 = 0, х2 = 3, х3 = 1 - последняя н входит в область определения функции. Используя достаточные признаки экстремума, выясним, как меняет знак  , содержащий точку
, содержащий точку  ;
;  . Так как при переходе через точку
. Так как при переходе через точку 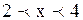 , содержащий точку х = 3.
, содержащий точку х = 3. ;
;  . Здесь производная меняет знак с «-» на «+», значит, х =3 – точка минимума функции
. Здесь производная меняет знак с «-» на «+», значит, х =3 – точка минимума функции  .
. и
и  , убывает на интервале (1;3).
, убывает на интервале (1;3). Критические точки второго рода, при которых
Критические точки второго рода, при которых  в нуль или существует, такие
в нуль или существует, такие  ,
,  , но эта последняя не входит в область определения функции. Остается точка х = 0. Проверим меняет ли знак
, но эта последняя не входит в область определения функции. Остается точка х = 0. Проверим меняет ли знак  при переходе через эту точку. Возьмем интервал (-1;
при переходе через эту точку. Возьмем интервал (-1;  ), содержащий точку х = 0. Вычислим
), содержащий точку х = 0. Вычислим  ,
,  . Отсюда следует, что х = 0 – точка перегиба,
. Отсюда следует, что х = 0 – точка перегиба, 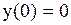 .
.  . Отсюда следует, что
. Отсюда следует, что  - интервал выпуклости;
- интервал выпуклости;  ,
,  - интервалы вогнутости кривой.
- интервалы вогнутости кривой.
 H0 MB = 200 – 80t,
NB = 50t,
cos600 =
H0 MB = 200 – 80t,
NB = 50t,
cos600 =  .
.
 ;
; км.
км. . Найдем первую производную по t:
. Найдем первую производную по t: . Приравнивая первую производную к нулю получим
. Приравнивая первую производную к нулю получим  откуда
откуда  или
или  - критическая точка.
- критическая точка. .
. . Следовательно, t0 = 1.6279 часа – точка минимума функции s. А так как других экстремумов эта функция не имеет, то в точке минимума функция имеет наименьшее значение:
. Следовательно, t0 = 1.6279 часа – точка минимума функции s. А так как других экстремумов эта функция не имеет, то в точке минимума функция имеет наименьшее значение:  .
.
 ;
;  . Составим полный дифференциал по формуле
. Составим полный дифференциал по формуле  .
. .
. .
.
 .
. .
.


 .
. и
и 
 x = 2y, 4y – y = -9, y = -3
x = 2y, 4y – y = -9, y = -3 и вычислим его значение в критической точке P(-9; -3). Тогда, если
и вычислим его значение в критической точке P(-9; -3). Тогда, если  , то P- точка экстремума. При этом, если
, то P- точка экстремума. При этом, если  , то Р – точка минимума,
, то Р – точка минимума, , то Р – точка максимума,
, то Р – точка максимума, , экстремума нет, а если
, экстремума нет, а если  - экстремум может быть, а может не быть. Нужны дополнительные исследования.
- экстремум может быть, а может не быть. Нужны дополнительные исследования. , следовательно, P(-9; -3)- точка экстремума, а так как
, следовательно, P(-9; -3)- точка экстремума, а так как  независимо от координат точки Р, то P(-9; -3) – точка минимума данной функции.
независимо от координат точки Р, то P(-9; -3) – точка минимума данной функции. , б)
, б)  ,
, , г)
, г)  , д)
, д)  .
. . Найдем дифференциалы обеих частей подстановки
. Найдем дифференциалы обеих частей подстановки 
 . Произведем замену переменной в подынтегральном выражении и найдем интеграл
. Произведем замену переменной в подынтегральном выражении и найдем интеграл  .
. .
. . откуда
. откуда  или
или  . Таким образом,
. Таким образом,  .
. .
. , где
, где 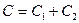 , две произвольные постоянные суммы неопределенных интегралов объединяют в одну.
, две произвольные постоянные суммы неопределенных интегралов объединяют в одну.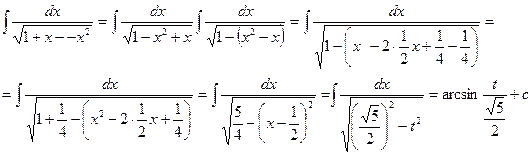

 . Возвращаясь к прежней переменной, будем иметь
. Возвращаясь к прежней переменной, будем иметь  .
. .
. ,
,  .
. , а во втором интегрируем, чтобы найти
, а во втором интегрируем, чтобы найти  . Получим
. Получим  ,
,  (здесь произвольную постоянную интегрирования принимаем равной нулю, поскольку достаточно хотя бы одного значения
(здесь произвольную постоянную интегрирования принимаем равной нулю, поскольку достаточно хотя бы одного значения  ).
). .
. на простейшие дроби по известному правилу, предварительно разложив знаменатель дроби на множители
на простейшие дроби по известному правилу, предварительно разложив знаменатель дроби на множители  . Тогда
. Тогда  , где A, B, M, N – неопределенные коэффициенты, которые надо найти. Приведя обе части последнего равенства к общему знаменателю, найдем
, где A, B, M, N – неопределенные коэффициенты, которые надо найти. Приведя обе части последнего равенства к общему знаменателю, найдем .
. .
. Решение системы:
Решение системы: 
 .
. ,
,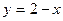 ,
,  (рис.2)
(рис.2) и примой
и примой  . Таким образом искомая площадь вычисляется с помощью определенного интеграла как сумма двух площадей по формуле
. Таким образом искомая площадь вычисляется с помощью определенного интеграла как сумма двух площадей по формуле 
 . Итак, площадь ОМА равна
. Итак, площадь ОМА равна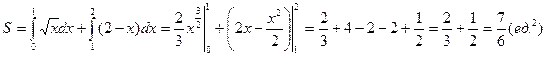 .
. фигуры, ограниченной линиями
фигуры, ограниченной линиями 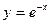 ,
,  ,
,  . (рис. 5).
. (рис. 5).
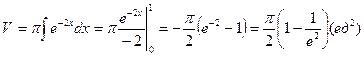
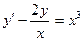 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям при
при  .
. . Будем искать решение в виде
. Будем искать решение в виде  , где
, где  ,
, 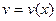 - дифференцируемые функции от
- дифференцируемые функции от  . Тогда
. Тогда  . Подставляя
. Подставляя  ,
, 
 .
. 
 или
или  , или
, или  . Интегрируя обе части уравнения, находим
. Интегрируя обе части уравнения, находим  или
или  (Здесь полагают произвольную постоянную равной нулю). Откуда
(Здесь полагают произвольную постоянную равной нулю). Откуда  . Подставляя его уравнение
. Подставляя его уравнение  или
или 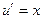 , или
, или  , или
, или  , откуда
, откуда  .
. . Это- общее решение, в котором
. Это- общее решение, в котором  - произвольная постоянная. Решим теперь задачу Коши: из общего решения по заданным начальным условиям определим частное решение. Для этого подставим в общее решение начальные условия. Получим
- произвольная постоянная. Решим теперь задачу Коши: из общего решения по заданным начальным условиям определим частное решение. Для этого подставим в общее решение начальные условия. Получим  или
или 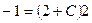 , или
, или  , или
, или  , откуда
, откуда  . Подставляя это значение постоянной в общее решение, получим частное решение
. Подставляя это значение постоянной в общее решение, получим частное решение  удовлетворяющее начальным условиям.
удовлетворяющее начальным условиям. .
. .
. . Радиус сходимости
. Радиус сходимости  . Тогда интервал сходимости
. Тогда интервал сходимости  . Исследуем сходимость ряда на концах этого интервала.
. Исследуем сходимость ряда на концах этого интервала. . Получим числовой ряд
. Получим числовой ряд  . Этот ряд является расходящимся, так как не выполняется необходимое условие его сходимости
. Этот ряд является расходящимся, так как не выполняется необходимое условие его сходимости  .
. , получим знакочередующийся числовой ряд
, получим знакочередующийся числовой ряд  , который расходится по той же причине: его общий член при
, который расходится по той же причине: его общий член при  стремится к 1, а не к 0.
стремится к 1, а не к 0.


