
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 13. Построение основных видов статистических графиковСодержание книги
Поиск на нашем сайте
Полем графика является место, на котором он выполняется. Оно характеризуется форматом. Графический образ – это символические знаки, с помощью которых изображаются статистические данные (линии, точки, прямоугольные фигуры и т.д.). Пространственные ориентиры определяют размещение графических образов на поле графика (декартовые, полярные координаты и т.д.). Масштаб графика – мера перевода численной величины в графическую. Экспликация графика - это пояснение его содержания, включающее заголовок, объяснение масштабных шкал, пояснение отдельных элементов графического образа, называемых легендой. К основным видам графиков относятся: линейные диаграммы, столбиковые диаграммы, ленточные (полосовые) графики, круговые диаграммы. Посредством построения линейных диаграмм формируется эмпирическая линия графика (статистическая кривая). При этом по оси абсцисс откладываются варианты или показатели времени, а по оси ординат значение изучаемого показателя (например, вес, стоимость, количество деклараций) По виду линейной диаграммы можно судить об изменении изучаемого явления во времени. Применение столбиковых и ленточных диаграмм позволяют наглядно представить статистическую информацию по атрибутивным рядам распределения. Количество столбиков - количество элементов ряда, а его высота значением анализируемого статистического показателя. (распределение объемов перемещаемых грузов по таможням, внешнеторговый оборот региона по субъектам РФ, входящим в регион). круговые диаграммы, - можно определить удельный вес (долю) составных частей анализируемого показателя от его общего объема(доля экспорта или импорта в общем объеме внешней торговли, распределение экспорта по отраслям промышленности...
Статистические показатели могут быть представлены абсолютными, относительными и средними величинами. Абсолютные показатели являются первичными, а относительные и средние – их производными. Абсолютные показатели выражают размеры, уровни, объемы, имеют натуральные и денежные измерения. Широкий спектр товаров, являющихся предметом внешней торговли измеряется в натуральных единицах: штуках, килограммах, куб. метрах. Неоднородным является и стоимостный показатель, т.к. оценивается в различных валютах. Абсолютные показатели подразделяются на индивидуальные и суммарные. Вес товара, содержащийся в одной ДТ, - индивидуальным, сумма веса товара по всем ДТ - суммарным абсолютным показателем. Абсолютные величины могут быть моментными или интервальными. Моментные абсолютные величины показывают уровень изучаемого явления или процесса на определенный момент времени или дату (стоимость основных фондов на первое число месяца). Интервальные — это итоговый накопленный результат за определ.период (интервал) времени (зарплата за месяц, квартал или год). Интервальные абсолютные величины, в отличие от моментных, допускают последующее суммирование. Абсолютная статистическая величина обозначается X, а их общее число в статистической совокупности — N. Количество величин с одинаковым значением признака обозначается f - частота (повторяемость, встречаемость). Cами по себе абсолютные статистические величины не дают полного представления об изучаемом явлении, т.к. не показывают его динамику, структуру, соотношение частей. А относительные …
Относительные величины Относительные величины представляют собой частное от деления двух величин и характеризуют количественное соотношение между ними. При расчете относительных величин следует иметь в виду, что в числител е всегда находится показатель, отражающий то явление, которое изучается, а в знаменателе - показатель, с которым производится сравнение, принимаемый за основание или базу сравнения. В завис-ти от базы сравнения- результат отношения может быть выражен в форме коэффициента или %. Если значение основания или базы сравнения принимается за единицу (приравнивается к единице), то относительная величина (результат сравнения) является коэффициентом и показывает, во сколько раз изучаемая величина больше основания. (только если сравниваемая величина существенно больше той, с которой она сравнивается.) Если значение основания или базу сравнения принять за 100%, результат вычисления относительной величины будет выражаться также в %. По своему значению они подразделяются на относительные величины структуры, сравнения, динамики, интенсивности, координации. Относительные величины структуры характеризуют состав изучаемых совокупностей, исчисляются как отношение абсолютной величины каждого из элементов группировки к общему объему, т.е. как отношение части к целому. Сравнивая относительные величины структуры за разные периоды можно проследить структурные изменения. (Удел.вес (долю) экспорта и импорта в объеме внешнеторгового оборота…. а на долю экспорта – 3:4*100=75%). Относительные величины сравнения отражают количественное соотношение одноименных показателей, т.е. показывают во сколько раз (или на сколько %) один показатель больше (меньше) другого. (коэффициент покрытия импорта экспортом. - экспорт превышает импорт в.=3 раза.) Относительные величины динамики характеризуют изменение изучаемого явления во времени, т.е. показывают во сколько раз или на сколько %, уровень отчетного периода больше или меньше уровня базисного периода. (базис или цепной) интенсивности - сколько единиц одной совокупности приходится на единицу другой. Рассчитываются делением абсолютной величины одной совокупности изучаемого явления на величину, характеризующую объем среды.(На 1 сотрудника в год пришлось – 500 деклараций). координации - соотношение между отдельными частями стат. совокупности, и показывает во сколько раз сравниваемая часть больше или меньше части, которая принимается за базу сравнения. Относительная величина координации рассчитывается следующим образом.650: 6500= 10%, т.е. на 10 человек с высшим образованием приходится 1 чел. со средним техническим.
Средние величины сглаживание различий в величине признака, которые возникают по тем или иным причинам. Средняя величина - один из распространенных способов обобщений количественных показателей. Рассмотрим признак x (осредняемый признак), по которому необходимо найти среднее значение Сред. величина измер-ся в той же размер-ти, что и признак. Каждая средняя величина характеризует изучаемую совокупность по какому-либо одному признаку. суммарные * средняя арифметическая; * средняя геометрическая; * средняя гармоническая; Средняя арифметическая используется для характеристики абсолютных величин. 1. Если каждое значение признака в ряду встречается по одному разу, расчет производится по формуле простой (сумма всех значений, деленная на число этих значений n - количество значений.
2. Если одно и то же значение признака встречается несколько раз, используют формулу средней арифметической взвешенной. f i - частота повторения этого признака (вес товара). Среднее арифметическое рассчитывается по разному в дискретных и интервальных вариационных рядах. В дискретных рядах варианты признака умножаются на частоты, эти произведения суммируются и полученная сумма произведений делится на сумму частот. В интервальных рядах значение признака задано в виде интервалов, поэтому нужно перейти к дискретному. В качестве вариантов Xi используется середина соответствующих интервалов. - как полусумма нижней и верхней границ. Средней гармонической величинойназывают величину, рассчитанную из обратных значений варьирующего признака. Она применяется и как обобщающая характеристика относительных величин. Средняя гармоническая простая:
Средняя гармоническая взвешенная:
Средней геометрической принято именовать величину, исчисляемую как корень n –ной степени из произведения n отдельных вариантов признака. Она также обычно используется для характеристики относительных величин и рассчитывается по формуле:
В случаях, когда некоторые либо все варианты (коэффициенты темпов роста, например) относятся к периодам, не одинаковым по продолжительности:
где х - варианты; fi - веса;
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 669; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.15.111.109 (0.006 с.) |

 . Значения осредняемого признака представлены рядом индивидуальных значений или вариант (х1, х2, х3….хn) (например, вариационным рядом) с частотами индивидуальных значений (f1,f2,f3,…fn).
. Значения осредняемого признака представлены рядом индивидуальных значений или вариант (х1, х2, х3….хn) (например, вариационным рядом) с частотами индивидуальных значений (f1,f2,f3,…fn). , где x1,x2 – знач-я признака (цена)
, где x1,x2 – знач-я признака (цена) ,
,
 ,
, ,
,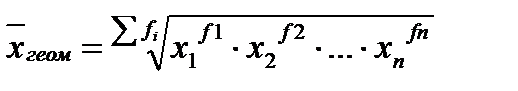 , (10.6)
, (10.6) - сумма весов.
- сумма весов.


