
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Средние показатели в рядах динамики.Содержание книги
Поиск на нашем сайте
Средние показатели динамики – средний уровень ряда, средние абсолютные изменения и ускорения, средние темпы роста – характеризуют тенденцию. Они необходимы при обобщении характеристик тенденции за длительный периода по различным периодам и незаменимы при сравнении развития за неодинаковые по длительности отрезки времени, при выборе аналитического выражения. 1)Средний уровень интервального ряда динамики определяется как простая арифметическая средняя из уровней за равные промежутки времени: 3)Средний абсолютный прирост (абсолютное изменение) определяется как простая арифметическая средняя из абсолютных изменений за равные промежутки времени (цепных абсолютных изменений) или как частное от деления базисного абсолютного изменения на число осредняемых отрезков времени от базисного до сравниваемого периода:
Укрупнение интервалов Укрупнение интервалов от квартальных до годовых (итоговая сумма), позволяет получить более наглядную тенденцию объема реализации продукции. Смысл приема заключается в том, что первоначальный ряд динамики преобразуется и заменяется другим, показатели которого относятся к большим по продолжительности периодам времени. Например, ряд, содержащий данные о квартальном объеме реализации продукции, может быть преобразован в ряд годовых данных. Вновь образованный ряд может содержать либо абсолютные величины за укрупненные по продолжительности промежутки времени (эти величины получаю путем простого суммирования уровней первоначального ряда абсолютных величин), либо средние величины. При суммировании уровней или при выявлении средних по укрупненным интервалам отклонения в уровнях, обусловленные случайными причинами, взаимопогашаются, сглаживаются и более четко обнаруживается действие основных факторов изменения уровней
Сглаживание скользящей средней Сглаживание скользящей средней – для этого метода необходимо установить количество уровней ряда по которому будет усредняться данный динамический ряд – квартальные – 4, данные по месяцам – 12. Для нашего примера расчет состоит в определении средних величин из четырех уровней ряда.
……………………………………………………..
При сглаживании почетному числу уровней скользящая средняя может быть отнесена только к середине между двумя датами, находящимися в середине интервала сглаживания
Выравнивание с помощью МНК Для нахождения неизвестных коэффициентов методом наименьших квадратов (МНК) можно составить систему нормальных уравнений для рассмотренных функций и решить их, определив неизвестные коэффициенты
Изучение сезонных явлений Под сезонными колебаниями понимается устойчивое колебание ряда динамики, повторяющееся через определенные периоды времени в течение года.
|
||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 273; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.195.30 (0.005 с.) |

 2)Средняя хронологическая (для моментного ряда). В моментном ряду смысл среднего уровня в том, что он характеризует уже не состояние объекта в отдельные моменты, а его среднее, обобщенное состояние между начальным и конечным моментом учета. Средняя хронологическая рассчитывается по формуле:
2)Средняя хронологическая (для моментного ряда). В моментном ряду смысл среднего уровня в том, что он характеризует уже не состояние объекта в отдельные моменты, а его среднее, обобщенное состояние между начальным и конечным моментом учета. Средняя хронологическая рассчитывается по формуле: 
 4)Среднегодовой темп роста вычисляется по формуле средней геометрической:
4)Среднегодовой темп роста вычисляется по формуле средней геометрической:  или
или  где m – число коэффициентов роста. 5)Средний темп прироста определяется по формуле:
где m – число коэффициентов роста. 5)Средний темп прироста определяется по формуле: 



 ,
,  и
и  . Рассмотрим пример составления системы нормальных уравнений для гиперболической функции. МНК минимизирует сумму квадратов отклонений (
. Рассмотрим пример составления системы нормальных уравнений для гиперболической функции. МНК минимизирует сумму квадратов отклонений ( ) наблюдаемых значений от теоретических. Символьно это можно записать так.
) наблюдаемых значений от теоретических. Символьно это можно записать так.  где
где  – наблюдаемые значения временного ряда;
– наблюдаемые значения временного ряда; 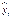 – теоретические значения временного ряда;
– теоретические значения временного ряда; 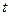 – временные отсчеты, например, годы
– временные отсчеты, например, годы  ;
;  – количество наблюдаемых значений временного ряда;
– количество наблюдаемых значений временного ряда;  – неизвестные коэффициенты.
– неизвестные коэффициенты. . После этого определяем индивидуальные индексы сезонности по формуле.
. После этого определяем индивидуальные индексы сезонности по формуле. 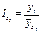 Затем находим средние значения индивидуальных индексов сезонностей по формуле.
Затем находим средние значения индивидуальных индексов сезонностей по формуле.  где
где  Затем определяют теоретические значения тренда
Затем определяют теоретические значения тренда 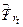 по приведенным выше функциям от времени. Для осуществления прогноза может быть использована следующая модель
по приведенным выше функциям от времени. Для осуществления прогноза может быть использована следующая модель 



