
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Абсолютні міри варіації: розмах варіації, середнє лінійне та середнє квадратичне відхилення. Формули розрахунку та економічний зміст.Содержание книги
Поиск на нашем сайте
Размах вариации – разность между max и min значением признака R=X max - X min «+» - простота расчета, интерпретация результатов«-» - данный показатель не дает представления о степени вариации в середине совокупности т.к. рассчитывается только на основании 2-х крайних значений; не учитывает частот в вариационном ряду Пример: в данной совокупности max стаж работника отклоняется от min на 2 года Среднее линейное отклонение представляет собой среднюю арифм из абсолютных значений отклонений отдельных вариантов, от их средней арифметической Л= Пример: В данной совокупности стаж отдельных работников отклоняется от среднего стажа в среднем по модулю на 3 года Среднее кв отклонение характеризует степень абсолютного колебания признака относительно средней величины и рассчитывается как корень квадратный из дисперсии δ= Например: в данной совокупности стаж отд работников отклоняется от среднего стажа в среднем на 5 лет в ту или иную сторону. Все показатели х-вали меру абсолютной колеблимости признаков, т.е. выражались в ед. измерения варьирующего признака.
18Формули розрахунку дисперсії (проста та зважена), коли кожна з них використовується? Дисперсия – средний квадрат отклонений отдельных значений признака от их средней арифметической. Дисперсия простая: Дисперсия взвешенная: Дисперсия является безразмерным показателем. Коефіцієнти варіації, їх роль у статистичному аналізі. Для характеристики колеблимости признака рассчитывают коэффициенты вариации: 1Линейный коэффициент вариации Vл = Например: в данной совокупности стаж отдельных работников отклоняется от среднего стажа работников среднем по модулю на 7% 2Квадратический Vδ= Статистическая совокупность считается количественно-однородной, если Vδ Например: в данной совокупности стаж отд работников отклоняется от среднего стажа в среднем на 55% в ту или иную, так как рассчитанный коэф вариации > 33%, то данная совокупность явл количественно неоднородной и рассчитанная средняя величина не явл типичной для данной совокупности.
позволяет сравнивать вариацию одного признака в разных совокупностей или вариацию нескольких признаков в одной совокупности Поняття моди в статистиці та формула розрахунку моди для інтервального варіаційного ряду. Модой в ст наз. наиболее часто встречающееся значение признака. В интервальных вариационных рядах сначала определяется модальный интервал, т.е. интервал, обладающий наибольшей частотой и частостью. А значение моды рассчитывается по ф-ле Мо = Хмо + Хмо – нижняя граница модального инт. Hмо – ширина мод инт Fмо – частота мод инт
Поняття медіани в статистиці та формула розрахунку медіани для інтервального варіаційного ряду. Медианой в ст наз. значение признака, который делит упорядоченный ряд пополам, при чем первая половина значения признака меньше медианы, а вторая свыше. В инт вар ряду медиана рассчитывается по ф-ле Ме = Хме – нижняя граница мед инт hме – ширина мед инт Sме-1 – накопленная частота предмедиан. инт fме – частота мед. инт. Расчет медианы начинается с нахождения медианного инт для чего находят накопленные частоты. Медианным инт будет тот интервал, где сумма накопленных частот превышает полу сумму частот ряда.
Квартилі та децилі: поняття, формули розрахунку для інтервального варіаційного ряду. Для изучения структуры вариационного ряда рассчитываются квартили и децили. Квартили делят ряд на 4 части, но рассчитывают 3 квартиля. Qi =xQi+ і-номер квартиля ХQi-нижние границы соответствующих кварт инт Децили делят ряд на 10 частей, но рассчитывают 9 децилей. Di =xQi+
|
|||||
|
Последнее изменение этой страницы: 2016-04-20; просмотров: 326; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.153.240 (0.007 с.) |

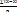 – для не сгруппированных Л=
– для не сгруппированных Л= 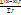 - для сгруппированных
- для сгруппированных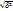 =
= 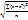 – для не сгруппированных δ=
– для не сгруппированных δ= 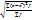 - для сгруппированных
- для сгруппированных =
= 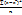 - для не сгруппированных данных
- для не сгруппированных данных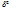 =
= 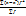 - для сгруппированных данных (для вариационного ряда)
- для сгруппированных данных (для вариационного ряда) *100 – процентное отношение среднего линейного отклонения средней арифметической
*100 – процентное отношение среднего линейного отклонения средней арифметической * 100
* 100 33%
33%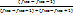 *hмо
*hмо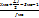 * hме
* hме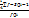 *hQi
*hQi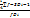 *hDi
*hDi


