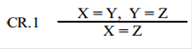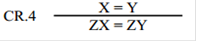Комбинаторная логика: алфавит

Рассмотрим алфавит комбинаторной логики.

Допускаются элементы четырех видов:

1) константы;

2) переменные;

3) комбинаторные выражения (или, иначе, термы);

4) специальные символы.

При этом принимаются следующие обозначения.

Константы( остающееся неизменным при всех изменениях ирасчетах ): c1, c2, … обозначаются малыми буквами латинского алфавита, возможно, с индексами.

Переменные( величина, которая может принимать в процессе своего изменения различные значения ): x, y, … обозначаются малыми буквами латинского алфавита, возможно, с индексами.

Выражения (термы): M, N, … обозначаются заглавными буквами латинского алфавита, возможно, с индексами.

Допускается использование следующих специальных символов (взяты в кавычки и разделены запятыми): “(“, “)”.

 

 

Комбинаторная логика: построение термов

Рассмотрим далее порядок конструирования допустимых для заданного алфавита комбинаторных выражений, или, иначе, термов Определение. Пусть М – непустое множество. Тогда n- местным предикатом, заданным на М, называется выражение, содержащее n переменных и обращающееся в высказывание при замене этих переменных элементами множества М.

Рассмотрим примеры. Пусть М есть множество натуральных чисел N. Тогда выражения «x – простое число», «x – четное число», «x – больше 10» являются одноместными предикатами. При подстановке вместо x натуральных чисел получаются высказывания: «2 – простое число», «6 – простое число», «3 – четное число», «5 больше 10» и т.д. Выражения «x больше y», «x делит y нацело», «x плюс y равно 10» являются двухместными предикатами. (Конечно, последнее выражение можно было записать и так: «x+y=10»). Примеры трехместных предикатов, заданных на множестве натуральных чисел: число z лежит между «x и y», «x плюс y равно z», «|x-y|z».).

Комбинаторные термы строятся по индукции (порядок построения можно считать определением) следующим образом:

Базис индукции: любая переменная или константа является комбинаторным термом по определению.

Шаг индукции: если M, N – произвольные комбинаторные термы и x – произвольная переменная, то справедливо, что:

• выражение (MN) является допустимым комбинаторным термом.

Заметим, что при этом комбинаторное выражение (MN) обозначает операцию аппликации (или применения функции к аргументу).

Операции абстракции в комбинаторной логике не существует.

Кроме того, примем, что никакой другой набор символов не является допустимым комбинаторным термом.

 

 

Комбинаторная логика: аксиомы

После определения алфавита и порядка построения допустимых комбинаторных выражений посредством операции аппликации, перечислим аксиомы комбинаторной логики.

Отметим, что употребляемый ниже символ “=” понимается в комбинаторной логике как обозначение отношения конвертируемости, которым связываются соединенные этим значком комбинаторные термы. Конвертируемость двух комбинаторных термов означает, что один комбинаторный терм может быть преобразован к другому. Отношение конвертируемости моделирует переобозначения и во многих отношениях, как отмечалось ранее, напоминает процесс программирования.

Следующие аксиомы задают свойства отношения конвертируемости:

(I) Ix = x;

(K) Kxy = x;

(S) Sxyz = xz(yz).

Правила вывода

Комбинаторная логика - это теория с единственным предикатом равенства, и все ее формулы имеют вид равенства двух термов. Смысл аксиом и правил вывода очевиден.

(I) - аксиома рефлексивности равенства, а правила CR.1 и CR.2 - его

транзитивность и симметричность.

Оставшиеся два правила CR.3 и CR.4 - это конгруэнтность равенства.

Аксиомы (K) и (S) постулируют существование двух базисных преобразований

 

Аксиома (I) означает существование комбинатора (функции) тождества, т.е. наличие тождественного преобразования, при котором любой аргумент отображается сам в себя.

Аксиома (K) означает существование комбинатора (функции) взятия первой проекции, т.е. первого элемента упорядоченной пары или первого элемента списка. Интуитивно ясно, что эта аксиома близка языкам функционального программирования, оперирующим списками, и соответствует фундаментальной операции взятия головного (первого) элемента списка.

Если восстановить опущенные скобки, они примут вид

((Kx)y) = x

(((Sx)y)z) = ((xz)(yz))

С их помощью можно определять другие комбинаторы. Например, комбинатор тождественного преобразования, который в применении к любому терму x оставляет его неизменным, можно определить как SKK

SKKx=Kx(Kx)=x

В качестве другого примера можно привести комбинатор K(SKK), реализующий функцию проекции на второй аргумент:

K(SKK)xy=SKKy=Ky(Ky)=y

 

Несколько проще это же преобразование можно задать с помощью комбинатора SK:

SKxy=Ky(xy)=y

 

Таким образом, одно и то же соотношение вход-выход можно представить в языке комбинаторной логики различными алгоритмическими преобразованиями.

В качестве дополнительной иллюстрации покажем, как средствами комбинаторной логики представить свойство коммутативности сложения.

x+y=y+x

 

Легко проверить, что комбинатор S(S(KS)(S(KK)S))(KS), который мы для

краткости обозначим посредством C, осуществляет следующее преобразование.

Cxyz=xzy

 

Свойство коммутативности сложения в аппликативной записи имеет вид

 

Axy=Ayx.

 

Поскольку CAxy=Ayx, то же самое может быть представлено как Axy=CAxy. Так как переменные x и y играют лишь вспомогательную роль, они могут быть опущены. Результирующая запись, выражающая коммутативность операции A,выглядит очень просто.

A=CA

 

Никакие переменные не нужны, поскольку по правилам комбинаторной логики для любых двух термов X и Y из A=CA выводимо AXY=AYX.

A=CA ⇒ AX=CAX ⇒ AXY=CAXY ⇒ AXY=AYX