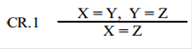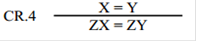Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
По предмету: Дискретная математикаСодержание книги
Поиск на нашем сайте
РЕФЕРАТ По предмету: Дискретная математика
тема: Комбинаторная логика как формальная система
Выполнили: студентки 2 курса 23 группы Рашидова Татьяна Козлова Кристина
Орел
Содержание 1. Определение комбинатора 2. Комбинаторная логика как формальная система: алфавит, аксиомы, правила вывода Комбинаторная логика: алфавит Комбинаторная логика: построение термов Комбинаторная логика: аксиомы Комбинаторная логика: правила вывода 3. Примеры комбинаторов Соглашения об обозначениях Синтаксис комбинаторной логики Редукция комбинаторов 4. Определение базиса. Основные базисы комбинаторной логики 5. Приписывание типов комбинаторам. Выводимость типов 6. Примеры функций базисных комбинаторов на SML 7. Библиография
Введение В ходе реферата будут рассмотрены важнейшие научные исследования, относящиеся к эволюции подходов к математическому моделированию ключевой сущности функционального подхода к программированию, а именно, функции. При этом будет особо отмечено то обстоятельство, что (типизированные) функции языков программирования естественным и интуитивно понятным образом моделируются посредством комбинаторов – ламбда-выражений специального вида (с приписанными им типами). Далее будет представлено формальное введение в типизированный вариант комбинаторной логики, первоначально предложенный Х. Карри. Изложение формальной теории будет производиться в традиционной для математики последовательности: алфавит, аксиомы и правила вывода. Затем будет обсуждаться понятие базисного набора комбинаторов: будут рассмотрены несколько вариантов базисов, включая минимально возможный. По результатам представленной теории будут сделаны выводы о преимуществах и недостатках комбинаторной логики для моделирования конструкций языков функционального программирования со строгой типизацией. При этом существенное внимание будет уделено формализации языка функционального программирования SML, который изучается на протяжении всего курса, в частности, вопросу выводимости типов.
Определение комбинатора Переменная x называется свободной в ламбда-выражении(терме) вида λx.A, если она не имеет вхождений в терм A; в противном случае переменная x называется связанной. Для составных термов понятие связанной и свободной переменной определяется индукцией по построению с учетом возможных способов комбинирования, а именно, операций аппликации и абстракции. Аппликация означает применение или вызов функции по отношению к заданному значению. Её обычно обозначают Абстракция или λ-абстракция в свою очередь строит функции по заданным выражениям. Именно, если Примеры: λx.(xx), λx.((xz) λy((yy)x))
Терм, не содержащий свободных переменных, называется комбинатором.
Комбинаторная логика как формальная система: алфавит, аксиомы, правила вывода Перейдем к описанию комбинаторной логики как формальной системы. Согласно математической практике, необходимо определить следующие элементы теории: Алфавит – множество допустимых символов. Утверждения – правила образования терминальных символов. Аксиомы – элементарные утверждения, истинность, которых принимается без доказательства. Правила вывода – правила преобразования одних символов (объектов) языка в другие.
Правила вывода
Комбинаторная логика - это теория с единственным предикатом равенства, и все ее формулы имеют вид равенства двух термов. Смысл аксиом и правил вывода очевиден. (I) - аксиома рефлексивности равенства, а правила CR.1 и CR.2 - его транзитивность и симметричность. Оставшиеся два правила CR.3 и CR.4 - это конгруэнтность равенства. Аксиомы (K) и (S) постулируют существование двух базисных преобразований
Аксиома (I) означает существование комбинатора (функции) тождества, т.е. наличие тождественного преобразования, при котором любой аргумент отображается сам в себя. Аксиома (K) означает существование комбинатора (функции) взятия первой проекции, т.е. первого элемента упорядоченной пары или первого элемента списка. Интуитивно ясно, что эта аксиома близка языкам функционального программирования, оперирующим списками, и соответствует фундаментальной операции взятия головного (первого) элемента списка. Если восстановить опущенные скобки, они примут вид ((Kx)y) = x (((Sx)y)z) = ((xz)(yz)) С их помощью можно определять другие комбинаторы. Например, комбинатор тождественного преобразования, который в применении к любому терму x оставляет его неизменным, можно определить как SKK SKKx=Kx(Kx)=x В качестве другого примера можно привести комбинатор K(SKK), реализующий функцию проекции на второй аргумент: K(SKK)xy=SKKy=Ky(Ky)=y
Несколько проще это же преобразование можно задать с помощью комбинатора SK: SKxy=Ky(xy)=y
Таким образом, одно и то же соотношение вход-выход можно представить в языке комбинаторной логики различными алгоритмическими преобразованиями. В качестве дополнительной иллюстрации покажем, как средствами комбинаторной логики представить свойство коммутативности сложения. x+y=y+x
Легко проверить, что комбинатор S(S(KS)(S(KK)S))(KS), который мы для краткости обозначим посредством C, осуществляет следующее преобразование. Cxyz=xzy
Свойство коммутативности сложения в аппликативной записи имеет вид
Axy=Ayx.
Поскольку CAxy=Ayx, то же самое может быть представлено как Axy=CAxy. Так как переменные x и y играют лишь вспомогательную роль, они могут быть опущены. Результирующая запись, выражающая коммутативность операции A,выглядит очень просто. A=CA
Никакие переменные не нужны, поскольку по правилам комбинаторной логики для любых двух термов X и Y из A=CA выводимо AXY=AYX. A=CA ⇒ AX=CAX ⇒ AXY=CAXY ⇒ AXY=AYX
Примеры комбинаторов Проиллюстрируем представленную формальную систему комбинаторной логики необходимыми примерами комбинаторов. Рассмотрим характеристические соотношения для комбинаторов, которые впоследствии окажутся теоретически интересными и практически полезными в данном курсе (некоторые из соотношений совпадают с введенными ранее аксиомами): (I) I a = a; Соотношение (I), как уже отмечалось, характеризует комбинатор тождества. (K) К ab = a; Соотношение (K) характеризует комбинатор первой проекции (иначе именуемый канцелятором, т.е. «отменяющим» «выполнение» всех «инструкций», кроме первой). (S) S abc = ac(bc); Соотношение (S) характеризует комбинатор- коннектор, который определяет порядок «связывания» «инструкций» программы таким образом, что третья «инструкция» «распределяется» по паре из двух первых. (B) B abc = a(bc); Соотношение (B) характеризует комбинатор композиции, который образует последовательность комбинаторных термов и служит для объединения более элементарных «инструкций» в более сложные, а в итоге – в «программы». (C) C abc = acb; (W) W xy = xyy. Соотношения (C) и (W) определяют соответственно пермутацию (перестановку) и дублирование аргументов.
Соглашения об обозначениях К сожалению, относительная простота описания предыдущих этапов формальной теории комбинаторной логики (алфавита, аксиом и правил вывода) порождает довольно громоздкие выкладки при моделировании вычислений. В этой связи из соображения экономии пространства для вывода соотношений принимаются следующие умолчания, позволяющие значительно сократить запись и увеличить удобство прочтения и обработки комбинаторных термов. Во-первых, скобки для операции аппликации восстанавливаются по ассоциации влево, например: X Y = (X Y), X Y Z = ((X Y) Z), … Во-вторых, избыточные скобки могут опускаться, например: (X Y) = X Y, ((X Y) Z) = X Y Z, …
Редукция комбинаторов Редукция (преобразование для сокращения записи) комбинаторных термов возможна в соответствии с правилами вывода, аналогичным аксиомам (K) и (S). Напомним, что одной из основных причин возникновения ламбда-исчисления была необходимость исследовать возможность кратчайшей перезаписи выражения (функции) с сохранением эквивалентного значения. Для реализации этой возможности вводилось преобразование редукции ламбда-термов. Оказывается, что в комбинаторной логике наследуется возможность редукции. Поскольку она интересна теоретически (для сокращения выкладок) и полезна практически (для оптимизации программного кода абстрактных) машин, рассмотрим ее более подробно. В ходе исследований было выяснено, что редукция (преобразование для сокращения записи) комбинаторных термов возможна в соответствии с правилами вывода, аналогичными аксиомам (K) и (S). Проиллюстрируем моделирование механизма редукции следующим примером. Пример. Рассмотрим комбинаторный терм вида S K K x. Пользуясь аксиомами (К) и (S), а также правилами вывода, произведем редукцию терма: S K K x = (по правилу S) = K x (K x) = (по правилу K) x. В результате получаем, что S K K x = x, откуда, с учетом аксиом и правила (I), I = SKK
Базисы комбинаторов Множество (минимальной мощности) комбинаторов, через элементы которого выразим произвольный комбинатор, называется (минимальным) базисом. Минимальный базис: {K,S}. Другие примеры базисов: {I,K,S}; {I,B,C,S}; {B,W,K}. Примеры. Разложение термов в базисе {K,S}: B = S(KS)K; W = SS(K(SKK)); C = S(BBS)(KK). Разложение в базисе – аналог программирования. Как видно из предыдущего примера, одни комбинаторы можно выразить через другие. Возникает вопрос: существует ли некоторый конечный набор комбинаторов, посредством которого возможно выразить произвольный терм комбинаторной логики? Оказывается, что ответ на поставленный вопрос утвердительный, причем введенные аксиомы и правила вывода обеспечивают весьма лаконичный набор такого рода. Необходимость продолжения рассуждений приводит нас к понятию базиса. Множество (минимальной мощности) комбинаторов, через элементы которого выразим произвольный комбинатор, называется (минимальным) базисом. Как оказывается, можно доказать, что: 1) базис термов для комбинаторной логики действительно существует (причем существует бесконечное множество возможных базисов); 2) для любого базиса справедливо, что он обеспечивает представление произвольного комбинаторного терма (в силу свойства полноты, которым обладает система комбинаторной логики); 3) минимальный базис состоит всего из двух «инструкций»-комбинаторов, например, {K,S}.
Приведем еще несколько примеров базисов: {I,K,S}; {I,B,C,S}; {B,W,K}. Разложение термов в базисе {K,S} для ранее рассмотренных комбинаторов имеет вид: B = S(KS)K; W = SS(K(SKK)); C = S(BBS)(KK). Разложение в базисе аналогично программированию на языке базисных инструкций.
Библиография 1) Комбинаторная логика как формальная система © Учебный Центр безопасности информационных технологий Microsoft Московского инженерно-физического института (государственного университета), 2003г. 2) Доклад на заседании научно-исследовательского семинара сектора логики Института философии РАН. 6 мая 2010 г.
РЕФЕРАТ по предмету: Дискретная математика
тема: Комбинаторная логика как формальная система
Выполнили: студентки 2 курса 23 группы Рашидова Татьяна Козлова Кристина
Орел
Содержание 1. Определение комбинатора 2. Комбинаторная логика как формальная система: алфавит, аксиомы, правила вывода
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 510; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.206.141 (0.009 с.) |

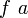
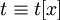 — выражение, свободно содержащее x, тогда запись
— выражение, свободно содержащее x, тогда запись  означает: λ функция от аргумента x, которая имеет вид t) обозначает функцию
означает: λ функция от аргумента x, которая имеет вид t) обозначает функцию  . Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы x свободно входило в t, не очень существенно — достаточно предположить, что
. Таким образом, с помощью абстракции можно конструировать новые функции. Требование, чтобы x свободно входило в t, не очень существенно — достаточно предположить, что  , если это не так.
, если это не так.