Дайте определение равнозначных понятий.

Равнозначными (или тождественными; равнообъемными) называются понятия, которые различаются по своему содержанию, но объемы которых совпадают.

Множество предметов, которое мыслится в понятии, называется объемом понятия. Объем понятия «преступление» охватывает все преступления, поскольку они имеют общие существенные признаки.

Совпадение объемов- это когда все элементы объема данного понятия полностью исчерпывают объем другого понятия (например, «квадрат» и «прямоугольник с равными сторонами»; «река Волга» и «самая длинная река в Европе».

 

31. Подчинение понятий (subordinatio notionurn) мы имеем в том случае, когда одно понятие относится к другому, как вид к своему роду, когда одно понятие входит в объём другого как часть его объема. Для примера возьмём понятие «дерево» А и понятие «берёза» В. Последнее понятие входит в объём первого. (Символ подчинения понятий см. на рис. 4.) Другие примеры: «духовная деятельность», «ощу­щение вкуса», «человек», «математик».

32. Скрещивающиеся понятия (notiones inter se convenientes). Если мы имеем два понятия, содержание которых различно, но объёмы некоторыми своими частями совпадают, то такие два понятия на­зываются скрещивающимися. Возьмём два понятия, например А — «писатели» и В — «учёные». В объёме понятия «писатели» заключается часть объёма понятия «учёные», ибо некоторые пи­сатели суть учёные, и, с другой сторо­ны, в объёме понятия «учёные» заключается некоторая часть объёма поня­тия «писатели», ибо некоторые из учёных суть писатели. Это мы могли бы изобразить при помощи схемы на рис. 9.

Так как та часть объёма понятия «писатели», которая состоит из учёных, и та часть объёма понятия «учёные», которая состоит из писателей, логически между собой равны, то символически их можно представить равными частями двух кругов, которые при наложении могли бы совпасть. Поэтому схемой скрещиваю­щихся понятий могут служить два скрещивающихся круга, причём круги символизируют объёмы данных понятий, а место их скрещивания — совпадающие, логически равные части этих объёмов. Другой пример — прямоугольные фигуры и параллелограммы, ибо некоторые прямоугольные фигуры суть параллелограммы и некоторые параллелограммы суть прямоугольные фи­гуры.

 

33. Соподчинение понятий (c oordinatio notionum) мы имеем в том случае, если а объём одного и того же более широкого понятия входят два иди несколько одинаково подчинённых ему низших понятий. Эти низшие понятия называются соподчи­нёнными (координированными). Напри­мер, «мужество» В, «умеренность» С, «добродетель» А. Оба первых понятия входят в объём последнего (рис. 5).

Рис. 5.

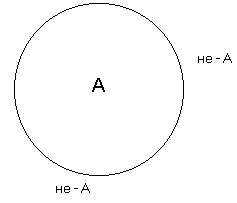
2. 34. Приведите пример двух понятий, находящихся в отношении противоречия (контрадикторности), объясните суть этого отношения.

Если мы имеем какое-нибудь понятие А и другое понятие В, относительно которого известно только то, что оно не есть А, то такие понятия называются противоречащими (contradictoriae). Например, понятия «белый» и «небелый» суть понятия противо­речащие. Итак, два термина, из которых один получен путём прибавления отрицательной частицы «не» к другому, относятся между собой, как противореча­щие. Символически отношение между противоречащими поня­тиями выражается следующим образом (рис. 8). Кругом сим­волизируется какое-нибудь одно понятие А, и вне его ставится другое понятие В, которое есть не-А, причём это понятие В может быть поставлено где угодно, лишь бы не внутри круга, не в его объёме; это второе понятие по своим свойствам называется понятием отрицательным или нёопредёленным (notio negativa seu indefinita).

35. Объясните на примере отношение противоположности понятий.

Если мы возьмём объём какого-нибудь понятия и будем рас­пределять по степени сходства виды, входящие в него, таким образом, что после каждого вида мы будем брать следующий, наименее от него отличный, то в конце концов из этих понятий-видов получится ряд, в котором первый и последний члены очень сильно отличаются друг от друга. Эти-то два понятия, пер­вое и последнее, во взятом нами ряде видов находятся в отноше­нии противности или противоположности. Будем, например, указанным способом распределять виды понятия «цвет». В его объём входят различные оттенки всевозможных цветов: красного, зелёного, чёрного, белого, серого и т. п. Если мы указанным выше способом будем размещать виды в ряд по мере сходства их, то можем получить приблизительно следующий ряд: белый, беловатый, светло-серый, серый, темно-серый, черноватый, чёрный.

Рис. 7.

Рис. 8.

 

 

Как видно из этого, наибольшее различие здесь между понятиями «белый» и «чёрный»; они-то и суть противопо­ложные или противные понятия. Итак, понятия, входящие в один и тот же объём, но очень отличающиеся друг от Друга, назы­ваются противными (contrariae). Схема: в круге, символизирую­щем объём какого-нибудь понятия, двумя линиями отделены два крайних отрезка, один против другого (рис. 7). Другие примеры: «добрый», «злой»; «высокий», «низкий»; «красивый», «уродли­вый»; «громкий», «тихий»; «глубокий», «мелкий». Надо заме­тить, что не все понятия имеют противные им понятия. Напри­мер, понятие «голубой» не имеет противного ему понятия.

 

36. Покажите принципиальные отличия таких отношений между понятиями как противоположность и противоречие.

 

.Если мы возьмём для сравнения два понятия противополож­ные и два противоречащие:

«белый» — «чёрный» (противоположные), «белый» - «небелый» (противоречащие),

то мы можем наглядно убедиться, что разница между этими двумя логическими отношениями огромная: тогда как второй член первой пары (чёрный) имеет вполне определённое содержание, которое можно представить, второй член второй пары (небелый) такого определённого содержания не имеет. Его содержание отличается неопределённостью, т. е., употребляя слово «небелый», мы можем под ним понимать и красный, и зе­лёный, и синий, и даже большой, красивый, добрый и т. п.