Деление должно производиться только по одному основанию.

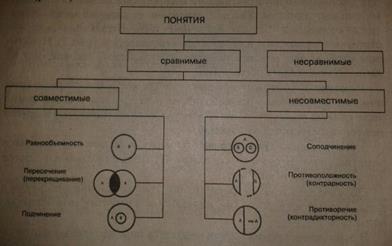
ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ.

Сравнимыми называются понятия, имеющие некоторые призна­ки, позволяющие эти понятия сравнивать друг с другом.

Несравнимыми называются понятия, не имеющие общих при­знаков, поэтому и сравнивать эти понятия невозможно.

Сравнимые понятия делятся на совместимые и несовместимые.

Совместимые понятия

Понятия, объемы которых полностью или частично совпадают, называются совместимыми. В содержании этих понятий нет при­знаков, исключающих совпадение их объемов. Существуют три вида отношений совместимости: 1) равнообъемность, 2) пересечение (перекрещивание) и 3) подчинение (субординация).

1. В отношении равнообъемности находятся понятия, в которых мыслится один и тот же предмет. Объемы этих понятий полностью совпадают. Эти понятия отражают один предмет мысли: равно­угольный (равносторонний) треугольник, их объемы полностью со­впадают, однако содержание различно, поскольку каждое из них содержит разные признаки треугольника.

Отношение между понятиями принято изображать с помощью круговых схем (кругом Эйлера), где каждый круг обозначает объем понятия, а каждая его точка — предмет, мыслимый в его объеме.

Например - студент и учащийся в высшей школе.

2. В отношении пересечения (перекрещивания) находятся поня­тия, объем одного из которых частично входит в объем другого. Содержание этих понятий различно.

Например - «летчик» и «космонавт»: некоторые летчики являются космонавтами, есть летчики, не являющиеся космонавтами, и есть космонавты, не являющиеся летчиками.

3. В отношении подчинения (субординации) находятся понятия, объем одного из которых полностью входит в объем другого, состав­ляя его часть.
например - понятие «цветок» есть род для вида «роза».

 

Несовместимые понятия

Понятия, объемы которых не совпадают ни полностью, ни час­тично, называются несовместимыми (или внеположными). Эти понятия содержат признаки, исключающие совпадение их объ­емов.

Существуют три вида отношений несовместимости: 1) соподчине­ние (координация), 2) противоположность (контрарность), 3) про­тиворечие (контрадикторность).

1. В отношении соподчинения (координации) находятся два или больше неперекрещивающихся понятий, подчиненных общему для них понятию. Понятия, находящиеся в отношении подчинения к обще­му для них понятию, называются соподчиненными.
Например - А дерево, В – дуб, С – берёза.

2. В отношении противоположности (контрарности) находятся понятия, одно из которых содержит некоторые признаки, а дру­гое — признаки, не совместимые с ними. Такие понятия называются противоположными (контрарными). Объемы двух противополож­ных понятий составляют в своей сумме лишь часть объема общего для них родового понятия, видами которого они являются и которо­му они соподчинены. Например - Хороший – Плохой, Белый – Чёрный

3. В отношении противоречия (контрадикторности) находятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки исключает.

Объемы двух противоречащих понятий составляют весь объем рода, видами которого они являются и которому они соподчи­нены.
например - А – белый, Не-А – не белый. Изображается с черточкой сверху Ā

ЛОГИЧЕСКИЕ ОПЕРАЦИИ С ПОНЯТИЯМИ –

ДЕЙСТВИЯ, КОТОРЫЕ МОЖНО СОВЕРШИТЬ ЛИБО С ОБЪЕМОМ ПОНЯТИЯ ЛИБОС ЕГО СОДЕРЖАНИЕМ ЛИБО И С ТЕМ И С ДРУГИМ ОДНОВРЕМЕННО.

I. Обобщить понятие — значит перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но с меньшим содержанием. Например, обобщая понятие «Минис­терство юстиции Российской Федерации», мы переходим к понятию «министерство юстиции». Объем нового (общего) понятия шире исходного (единичного) понятия; первое относится ко второму как индивид к виду. Вместе с тем содержание понятия, образованного в результате обобщения, уменьшилось, так как мы исключили его индивидуальные признаки.

Обобщение понятия не может быть беспредельным. Наиболее общими являются понятия с предельно широким объемом — кате­гории, например «материя», «сознание», «движение», «свойство», «отношение» и т.п. Категории не имеют родового понятия, обоб­щить их нельзя.

II. Ограничить понятие — значит перейти от понятия с ббльшим объемом, но с меньшим содержанием к понятию с меньшим объемом, но ббльшим содержанием. Иначе говоря, чтобы ограничить понятие «юрист», мы переходим к поня­тию «следователь», которое в свою очередь можем ограничить, об­разовав понятие «следователь прокуратуры». Пределом ограниче­ния понятия является единичное понятие.

III. Определение понятия – логическая операция, раскрывающая содержание понятия

Понятие, содержание которого требуется раскрыть, называется определяемым (дефиниендум); понятие, раскрывающее содержа­ние определяемого понятия, — определяющим (дефиниенс).

Виды определения

Определения делятся на:

1. Номинальным называется опре­деление, посредством которого взамен описания какого-либо пред­мета вводится новый термин (имя), объясняется значение термина, его происхождение и т.п.

Реальным называется определение, раскрывающее существен­ные признаки предмета.

2. По способу выявления содержания понятия определения де­лятся на явные и неявные. Явные определения раскрывают сущест­венные признаки предмета; к неявным относятся определение через отношение предмета к своей противоположности, контекстуальное, остенсивное и некоторые другие виды определений.

Правила определения

1. Определение должно быть соразмерным.

объем определяемого по­нятия был равен объему определяющего.Т.е., эти понятия должны находиться в отношении равно-объемности.

2. Определение не должно заключать в себе круга.

Если при определении мы прибегаем к другому понятию, кото­рое, в свою очередь, определяется при помощи первого, то такое определение содержит в себе круг. Разновидностью круга в определении является тавтология — ошибочное определение, в котором определяющее понятие повто­ряет определяемое. Тавтология, отличается от круга в определении меньшей сложностью построения. Опреде­ляющее понятие является повторением определяемого.

3. Определение должно быть ясным.

Оно должно указывать на известные признаки, не нуждающиеся в определении и не содержащие двусмысленности.

А. в определении не должно быть неизвестных слов и выражений

Б. в определении не должно быть метафор и иных художественных средств.

Демократия – вечно цветущее дерево народовластия.

4. Определение не должно быть отрицательным. Отрицательное определение не раскрывает определяемого поня­тия. Оно указывает, чем не является предмет, не указывая, чем он является.

Определяющее понятие – понятие, которое указывает на содержание определяемого – dfn
Определяемое понятие – понятие, содержание которого надо раскрыть - dfd

Возможные ошибки

1. Слишком широкого определения - объем определяющего понятия шире, чем объем определяемого. Такую ошибку мы допустили бы, определив, к примеру, ромб просто как плоский четырехугольник.

2. Слишком узкого определения - объем определяющего понятия уже объема определяемого. «Студент высшего учебного заведения – лицо, зачисленное на конкурсной основе для обучения по программам высшего образования».

3. «Как попало» или В одном отношении широкое, в другом узкое. Ящик – тара для хранения овощей. Но в ящиках хранят не только овощи, а овощи – не только в ящиках.

IV. Деления понятия – логическая операция, раскрывающая объем понятий.

Деление по видоизменению признака – деление понятия на виды по какому-то определенному основанию

Дихотомическое деление – деление на 2 вида, находящиеся в отношении противоречия.

Состав:

А. делимое понятие – понятие, объем которого раскрывается

Б. классы (члены) деления – результат деления

В. основания деления – признак, видоизменение которого используется для образования классов деления

Правила деления

1. Деление должно быть соразмерным.

Поэтому объем членов деления должен быть равен в своей сумме объему делимого понятия.

Ошибки в делении понятия.

1. 2 ошибки: а. лишние виды выделены (деление с лишними классами); б. неполное деление
2. Подмена основания деления
3. Получившиеся при делении классы являются совместимыми по объему понятия
4. Скачок в делении – деление, лишенное последовательности.

 

СУЖДЕНИЕ –

Состав простого суждения

1. Субъект -предмет мысли, то, о чем говорится в суждении

2. Предикат – то, что говорится о предмете мысли

3. Логическая связка – отношение субъекта и предиката

4. Кванторное слово – количественная характеристика области предметов, к которой относится суждение.

Виды простых суждений

1. Общеутвердительное суждение (А)— это суждение, общее по коли­честву и утвердительное по качеству. Все S есть P (каждый, любой)
2. Общеотрицательное суждение (Е) — суждение, общее по количе­ству и отрицательное по качеству. Ни одно S не есть Р
3. Частноутвердительное суждение (I) — суждение, частное по коли­честву и утвердительное по качеству. Некоторые S есть Р.
4. Частноотрцательное суждение (О) — суждение, частное по количе­ству и отрицательное по качеству. Некоторые S не есть Р. (многие, часть, большинство)

СЛОЖНЫЕ СУЖДЕНИЯ.

ВИДЫ СЛОЖНЫХ СУЖДЕНИЙ.

1. Конъюктивное суждение – суждение, состоящее из нескольких простых суждений, связанных логической связкой «и».

Правило – истинно тогда и только тогда, когда истинны все составляющие суждения

Грамматически союзы – а, но, да, а также, как и, хотя и, однако, несмотря их, одновременно, не только … но и, в то время как, зато.

1. Дизъюнкция

А. простая (нестрогая) дизъюнкция – суждение, в котором связка «или» употребляется в соединительно-разделительном значении.

Правило – истинно тогда и только тогда, когда истинно хотя бы одно из составляющих его суждения

Б. строгая дизъюнкция – суждение, в котором связка «или» употребляется в разделительном значении

Правило – истинно тогда и только тогда, когда составляющие его суждения имеют разные истинностные значения.

Грамматические союзы – или, либо, то ли.. то ли

1. Импликация – суждение, состоящее из 2 простых, связанных логической связкой «если … то»

Правило – ложно тогда, когда основание истинное, а следствие ложно

Грамматические союзы – тогда,когда; там где, постольку поскольку, так как, при наличии… следует, в случае … следует, следовательно, при условии… наступает.

1. Эквиваленция

Грамматические союзы – если и только если …, то…; лишь при условии что …, то; в том и только в том случае, когда …, тогда.

Правило – истинно тогда и только тогда, когда составляющие его суждения имеют одинаковые истинностные значения (оба истинны, оба ложны).

 

ИЗ Модульного теста

А. по правилам логического квадрата частично совместимые суждения не могут быть одновременно ложными

Б. субъект всегда нераспределен в частных суждениях

В. предикат всегда распределен в отрицательных суждениях

Г. субъект всегда распределен в общих суждениях

Д, качественная характеристика – логическая связка

Е. количественная характеристика – квантор (кванторное слово)

Ж. субъект – понятие о предмете суждения

З. предикат – понятие о признаке предмета

И. если сложное суждение ложно, тогда и только тогда, когда ложны все составляющие его суждения, то это СЛАБАЯ ДИЗЪЮНКЦИЯ

p	q	p q	p v q	p q	p q	p q
и	и	и	и	л	и	и
и	л	л	и	и	л	л
л	и	л	и	и	и	л
л	л	л	л	л	и	и

 

УМОЗАКЛЮЧЕНИЕ –

это форма мышления, посредством кото­рой из одного или нескольких суждений выводится новое суждение.

СТРУКТУРА УМОЗАКЛЮЧЕНИЯ

1. Посылка - исходные суждения, из кото­рых выводится новое суждение.
2. Заключение – новое суждение
3. Вывод – логический переход от посылки к заключению

 

ОПЕРАЦИИ

1. Превращение – суждение, в котором заключение является суждением, противоположным посылке, с предикатом, противоречащим предикату посылки

1. А в Е

А - Все S есть Р _________
Е - Ни одно S не есть не-Р

2.Е в А
е - Все S не есть Р
а- Все S есть не-Р

3.I превращается в О.

I - Некоторые S есть Р
О - Некоторые S не есть не-Р

 

4.О превращается в I.

О - Некоторые S не есть Р
I - Некоторые S есть не-Р

Обращение.

Преобразование суждения, в результате которого субъект ис­ходного суждения становится предикатом, а предикат — субъек­том заключения, называется обращением.

А I	Все S есть Р _________ Некоторые Р есть S
Е Е	Все S не есть Р Все Р не есть S
I I	Некоторые S есть Р Некоторые Р есть S
О	Некоторые S не есть Р – не превращается

 

3.Противопоставление предикату – превращение суждения, а затем обращение получившегося суждения.

А Е Е	Все S есть Р _________ Все S не есть не-Р Все не-Р не есть S
Е А I	Все S не есть Р Все S есть не-Р Некоторые не-Р есть S
I I	Некоторые S есть Р нельзя преобразовать противопоставление предикату
О I	Некоторые S не есть Р Некоторые не-Р есть S

4. противопоставление субъекту – обращение суждения и превращение получившегося суждения.

А I O	Все S есть Р _________ Некоторые Р есть S Некоторые Р не есть не-S
Е Е А	Все S не есть Р Все Р есть не- S Все Р есть не-S
I О	Некоторые S есть Р Некоторые Р не есть не-S
О	Некоторые S не есть Р нельзя преобразовать противопоставление субъекту

ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ –

УМОЗАКЛЮЧЕНИЕ, В КОТОРОМ УСТАНАВЛИВАЕТСЯ ОТНОШЕНИЕ КРАЙНИХ ТЕРМИНОВ К СРЕДНЕМУ

СОСТАВ

1. Я (М) – человек
2. Ты не я (м)
   Ты (S) не человек (Р)

ОБЩИЕ ПРАВИЛА ПКС

(ПРАВИЛА ТЕРМИНОВ).

1. в силлогизме должно быть только три термина.

2. средний термин должен быть распределен хотя бы в одной из посылок.

3. термин, не распределенный в посылке, не может быть распределен и в заключении.

ПРАВИЛА ПОСЫЛОК

1. хотя бы одна из посылок должна быть утверди­тельным суждением. Из двух отрицательных посылок заключение с необходимостью не следует.

2. если одна из посылок — отрицательное суждение, то и заключение должно быть отрицательным.

3. хотя бы одна из посылок должна быть общим суждением.

4. если одна из посылок — частное суждение, то и заключение должно быть частным.

 

ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ.

Сравнимыми называются понятия, имеющие некоторые призна­ки, позволяющие эти понятия сравнивать друг с другом.

Несравнимыми называются понятия, не имеющие общих при­знаков, поэтому и сравнивать эти понятия невозможно.

Сравнимые понятия делятся на совместимые и несовместимые.

Совместимые понятия

Понятия, объемы которых полностью или частично совпадают, называются совместимыми. В содержании этих понятий нет при­знаков, исключающих совпадение их объемов. Существуют три вида отношений совместимости: 1) равнообъемность, 2) пересечение (перекрещивание) и 3) подчинение (субординация).

1. В отношении равнообъемности находятся понятия, в которых мыслится один и тот же предмет. Объемы этих понятий полностью совпадают. Эти понятия отражают один предмет мысли: равно­угольный (равносторонний) треугольник, их объемы полностью со­впадают, однако содержание различно, поскольку каждое из них содержит разные признаки треугольника.

Отношение между понятиями принято изображать с помощью круговых схем (кругом Эйлера), где каждый круг обозначает объем понятия, а каждая его точка — предмет, мыслимый в его объеме.

Например - студент и учащийся в высшей школе.

2. В отношении пересечения (перекрещивания) находятся поня­тия, объем одного из которых частично входит в объем другого. Содержание этих понятий различно.

Например - «летчик» и «космонавт»: некоторые летчики являются космонавтами, есть летчики, не являющиеся космонавтами, и есть космонавты, не являющиеся летчиками.

3. В отношении подчинения (субординации) находятся понятия, объем одного из которых полностью входит в объем другого, состав­ляя его часть.
например - понятие «цветок» есть род для вида «роза».

 

Несовместимые понятия

Понятия, объемы которых не совпадают ни полностью, ни час­тично, называются несовместимыми (или внеположными). Эти понятия содержат признаки, исключающие совпадение их объ­емов.

Существуют три вида отношений несовместимости: 1) соподчине­ние (координация), 2) противоположность (контрарность), 3) про­тиворечие (контрадикторность).

1. В отношении соподчинения (координации) находятся два или больше неперекрещивающихся понятий, подчиненных общему для них понятию. Понятия, находящиеся в отношении подчинения к обще­му для них понятию, называются соподчиненными.
Например - А дерево, В – дуб, С – берёза.

2. В отношении противоположности (контрарности) находятся понятия, одно из которых содержит некоторые признаки, а дру­гое — признаки, не совместимые с ними. Такие понятия называются противоположными (контрарными). Объемы двух противополож­ных понятий составляют в своей сумме лишь часть объема общего для них родового понятия, видами которого они являются и которо­му они соподчинены. Например - Хороший – Плохой, Белый – Чёрный

3. В отношении противоречия (контрадикторности) находятся понятия, одно из которых содержит некоторые признаки, а другое эти же признаки исключает.

Объемы двух противоречащих понятий составляют весь объем рода, видами которого они являются и которому они соподчи­нены.
например - А – белый, Не-А – не белый. Изображается с черточкой сверху Ā

ЛОГИЧЕСКИЕ ОПЕРАЦИИ С ПОНЯТИЯМИ –

ДЕЙСТВИЯ, КОТОРЫЕ МОЖНО СОВЕРШИТЬ ЛИБО С ОБЪЕМОМ ПОНЯТИЯ ЛИБОС ЕГО СОДЕРЖАНИЕМ ЛИБО И С ТЕМ И С ДРУГИМ ОДНОВРЕМЕННО.

I. Обобщить понятие — значит перейти от понятия с меньшим объемом, но с большим содержанием к понятию с большим объемом, но с меньшим содержанием. Например, обобщая понятие «Минис­терство юстиции Российской Федерации», мы переходим к понятию «министерство юстиции». Объем нового (общего) понятия шире исходного (единичного) понятия; первое относится ко второму как индивид к виду. Вместе с тем содержание понятия, образованного в результате обобщения, уменьшилось, так как мы исключили его индивидуальные признаки.

Обобщение понятия не может быть беспредельным. Наиболее общими являются понятия с предельно широким объемом — кате­гории, например «материя», «сознание», «движение», «свойство», «отношение» и т.п. Категории не имеют родового понятия, обоб­щить их нельзя.

II. Ограничить понятие — значит перейти от понятия с ббльшим объемом, но с меньшим содержанием к понятию с меньшим объемом, но ббльшим содержанием. Иначе говоря, чтобы ограничить понятие «юрист», мы переходим к поня­тию «следователь», которое в свою очередь можем ограничить, об­разовав понятие «следователь прокуратуры». Пределом ограниче­ния понятия является единичное понятие.

III. Определение понятия – логическая операция, раскрывающая содержание понятия

Понятие, содержание которого требуется раскрыть, называется определяемым (дефиниендум); понятие, раскрывающее содержа­ние определяемого понятия, — определяющим (дефиниенс).

Виды определения

Определения делятся на:

1. Номинальным называется опре­деление, посредством которого взамен описания какого-либо пред­мета вводится новый термин (имя), объясняется значение термина, его происхождение и т.п.

Реальным называется определение, раскрывающее существен­ные признаки предмета.

2. По способу выявления содержания понятия определения де­лятся на явные и неявные. Явные определения раскрывают сущест­венные признаки предмета; к неявным относятся определение через отношение предмета к своей противоположности, контекстуальное, остенсивное и некоторые другие виды определений.

Правила определения

1. Определение должно быть соразмерным.

объем определяемого по­нятия был равен объему определяющего.Т.е., эти понятия должны находиться в отношении равно-объемности.

2. Определение не должно заключать в себе круга.

Если при определении мы прибегаем к другому понятию, кото­рое, в свою очередь, определяется при помощи первого, то такое определение содержит в себе круг. Разновидностью круга в определении является тавтология — ошибочное определение, в котором определяющее понятие повто­ряет определяемое. Тавтология, отличается от круга в определении меньшей сложностью построения. Опреде­ляющее понятие является повторением определяемого.

3. Определение должно быть ясным.

Оно должно указывать на известные признаки, не нуждающиеся в определении и не содержащие двусмысленности.

А. в определении не должно быть неизвестных слов и выражений

Б. в определении не должно быть метафор и иных художественных средств.

Демократия – вечно цветущее дерево народовластия.

4. Определение не должно быть отрицательным. Отрицательное определение не раскрывает определяемого поня­тия. Оно указывает, чем не является предмет, не указывая, чем он является.

Определяющее понятие – понятие, которое указывает на содержание определяемого – dfn
Определяемое понятие – понятие, содержание которого надо раскрыть - dfd

Возможные ошибки

1. Слишком широкого определения - объем определяющего понятия шире, чем объем определяемого. Такую ошибку мы допустили бы, определив, к примеру, ромб просто как плоский четырехугольник.

2. Слишком узкого определения - объем определяющего понятия уже объема определяемого. «Студент высшего учебного заведения – лицо, зачисленное на конкурсной основе для обучения по программам высшего образования».

3. «Как попало» или В одном отношении широкое, в другом узкое. Ящик – тара для хранения овощей. Но в ящиках хранят не только овощи, а овощи – не только в ящиках.

IV. Деления понятия – логическая операция, раскрывающая объем понятий.

Деление по видоизменению признака – деление понятия на виды по какому-то определенному основанию

Дихотомическое деление – деление на 2 вида, находящиеся в отношении противоречия.

Состав:

А. делимое понятие – понятие, объем которого раскрывается

Б. классы (члены) деления – результат деления

В. основания деления – признак, видоизменение которого используется для образования классов деления

Правила деления

1. Деление должно быть соразмерным.

Поэтому объем членов деления должен быть равен в своей сумме объему делимого понятия.

Деление должно производиться только по одному основанию.

В процессе деления избранный нами признак должен оставаться одним и тем же и не подменяться другим признаком. Например, граждан какой-либо страны в зависимости от поставленной задачи можно разделить по их социальному положению или национальнос­ти, профессии или полу. Но нельзя смешивать эти признаки и де­лить, скажем, граждан России на рабочих, русских, шахтеров и жен­щин.

3. Члены деления должны исключать друг друга. Если выбрано не одно основание, то члены деления — видовые понятия — будут находить­ся в отношении частичного совпадения. Подобный же результат получим при делении преступле­ний на умышленные, неосторожные и воинские. Деление всех сту­дентов института на заочников, первокурсников и спортсменов также приведет к нарушению данного правила.

4. Деление должно быть непрерывным.

В процессе деления родового понятия нужно переходить к бли­жайшим видам, не пропуская их. Но нельзя переходить от деления на виды одного порядка к делению на виды другого порядка, например делить преступления на преступления против личности, в сфере экономики, и утрату военного имущества.

Ошибки в делении понятия.

1. 2 ошибки: а. лишние виды выделены (деление с лишними классами); б. неполное деление
2. Подмена основания деления
3. Получившиеся при делении классы являются совместимыми по объему понятия
4. Скачок в делении – деление, лишенное последовательности.

 

СУЖДЕНИЕ –