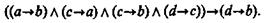Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сложный силлогизм. Части сложного силлогизма. Сориты.Содержание книги
Поиск на нашем сайте Полисиллогизмом (сложным силлогизмом) называются два или несколько простых категорических силлогизмов, связанных друг с другом таким образом, что заключение одного из них становится посылкой другого. Различают прогрессивные и регрессивные полисиллогизмы. В прогрессивном полисиллогизме заключение предшествующего силлогизма становится большей посылкой последующего силлогизма. Приведем пример прогрессивного полисиллогизма, представляющего собой цепь из трех силлогизмов и имеющего такую схему:
Возьмем полисиллогизм, состоящий из двух силлогизмов, и справа запишем его схему.
Разъясним получение схемы 2. Если общие категорические суждения заменить совпадающими с ними по смыслу условными суждениями, то второй полисиллогизм примет следующий вид: Если предмет есть металл, то он теплопроводен. Если предмет есть щелочноземельный металл, то он, конечно, металл. Если предмет есть щелочноземельный металл, то он теплопроводен. Если предмет есть кальций, то он щелочноземельный металл. Значит, если предмет есть кальций, то он теплопроводен. Выразив суждение «Предмет есть металл» буквой а, суждение «Предмет теплопроводен» — буквой b, суждение «Предмет есть щелочноземельный металл» — буквой с, суждение «Предмет есть кальций» — буквой d, мы получим схему 2.В виде правила вывода схему 2 данного прогрессивного полисиллогизма можно записать так:
где Это правило вывода путем преобразований можно перевести в формулу алгебры логики:
Эта формула тождественно-истинна, если все посылки полисиллогизма являются общими суждениями. Регрессивный полисиллогизм — это такой сложный силлогизм, в котором заключение предшествующего силлогизма становится меньшей посылкой последующего силлогизма.
1. Всеорганизмы (В) суть тела (С). 2. Все тела (С) имеют вес (D). Все растения (А) суть организмы (B) Все растения (А) суть тела (С). _____________________ _____________________ Все растения (А) суть тела (С). Все растения (А) имеют вес (D).
Запишем эти два силлогизма схематически: 1. Все В суть С. 2. Все С суть D. Все А суть В. Все А суть С. _______________ ____________ Все А суть С. Все А суть D.
Соединив их вместе и не повторяя дважды суждение «Все А суть С», мы получим схемы регрессивного полисиллогизма для общеутвердительных посылок:
В виде правила вывода последнюю схему можно записать так:
Это правило вывода путем преобразования можно перевести в формулу алгебры логики:
Сорит – полисиллогизм, в котором пропущена посылка последующего силлогизма, являющаяся выводом предыдущего. б) отрицающий-утверждающий Н: люди бывают европеоидами или монголоидами или негроидами
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 475; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.113 (0.006 с.) |




 — знак вывода.
— знак вывода.