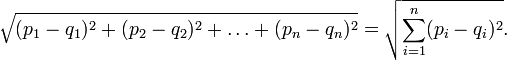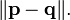Математичний алгоритм методу найближчих сусідів

Алгоритм методу найближчих сусідів в чомусь схожий з алгоритмом, використовуваним в методі кластеризації. Метод визначає відстань між невідомою точкою і всіма відомими точками даних. Визначення відстані - цілком тривіальна процедура, що легко виконується в рамках електронних таблиць, так що досить потужний комп'ютер впорається з цим завданням практично миттєво. Найпростіший і найбільш поширений спосіб визначення відстані - це нормалізована евклідова відстань.

 

Евклідова відстань (Евклідова метрика) — формула традиційної відстані між двома точками

та

для Евклідового простору:

Позначається

 

Опис звучить складніше, ніж власне обчислення. Звернемося до конкретного прикладу і спробуємо визначити, який товар схильний придбати покупець № 5.

Математична модель методу найближчих сусідів

Покупець Вік Дохід Куплений продукт1 45 46k Книга2 39 100k TV3 35 38k DVD4 69 150k Акустична система для автомобіля5 58 51k??? Крок 1: Формула для визначення відстаніВідстань = SQRT(((58 - Вік)/(69-35))^2) + ((51000 - Дохід)/(150000-38000))^2) Крок 2: Розрахунок балівПокуцпець Бали Куплений продукт1.385 Книга2.710 TV3.686 DVD4.941 Акустична система для автомобіля5 0.0???

Щоб відповісти на питання, який товар з найбільшою ймовірністю придбає покупець № 5, ми скористалися алгоритмом методу найближчих сусідів, наведеним вище, і отримали в результаті в якості найбільш вірогідної покупки книгу. Справа в тому, що відстань між покупцем № 5 і покупцем № 1 менше (значно менше), ніж відстань між покупцем № 5 і будь-яким іншим покупцем. Ґрунтуючись на цій моделі, можна стверджувати, що поведінка покупця № 5 з великою часткою ймовірності співпаде з поведінкою найближчого до нього покупця.

Однак корисність методу найближчих сусідів цим не вичерпується. Цей алгоритм може бути розширений таким чином, що замість одного найближчого сусіда можна було б визначати будь-яку кількість досить близьких відповідників. Таке розширення алгоритму називається N найближчих сусідів (наприклад, три найближчих сусіда). Наприклад, якщо в розглянутому вище прикладі потрібно визначити два найбільш вірогідних придбання покупця № 5, то відповідь буде книга іDVD. Якщо потрібно визначити 12 найбільш вірогідних покупок, то слід скористатися алгоритмом 12 найближчих сусідів.

Крім того, алгоритм не обмежується визначенням найбільш вірогідної покупки, він може бути використаний для отримання бінарної відповіді так/ні. Якщо в розглянутому вище прикладі ми замінимо значення в останньому стовпці на «Так, Ні, Так, Ні» (для покупців з першого по четвертий), то метод одного найближчого сусіда визначить «Так» у якості найбільш прогнозованої відповіді покупця № 5, метод двох найближчих сусідів теж видасть «Так» (покупці № 1 і № 3 відповіли «Так»), і метод трьох найближчих сусідів теж спрогнозує позитивну відповідь (покупці № 1 і № 3 відповіли «Так», покупець № 2 відповів «Ні», так що середнє значення дорівнює «Так»).

Останнє питання, на яке потрібно відповісти, перш ніж приступити до використання методу найближчих сусідів у практичних завданнях, це вирішити, скільки сусідів потрібно для нашої моделі. Ну що ж, не на всі питання можна легко знайти відповідь. Вам буде потрібно декілька експериментальних спроб для того, щоб визначити, яка кількість сусідів є оптимальною. Крім того, якщо ви використовуєте модель для отримання бінарного результату (0 або 1), то очевидно, що вам буде потрібна парна кількість сусідів.

 

Набір даних для WEKA

Набір даних, який ми будемо аналізувати методом найближчих сусідів, вам вже знайомий - це той же самий набір даних, який ми використовували для вивчення методу класифікації в попередній роботі, а саме, дані рекламної компанії вигаданого дилера BMW з продажу розширеної дворічної гарантії своїм постійним покупцям.

Наведемо тут ще раз короткий опис цього набору даних.

Дилерський центр має дані про 4500 продажів розширеної гарантії. Цей набір має такі атрибути:

· розподіл за доходами

[0 = $ 0 - $ 30k,

1 = $ 31k-$ 40k,

2 = $ 41k-$ 60k,

3 = $ 61k-$ 75k,

4 = $ 76k-$ 100k,

5 = $ 101k-$ 150k,

6 = $ 151k-$ 500k,

7 = $ 501k+],

· рік/місяць покупки першого автомобіля BMW,

· рік/місяць покупки останнього автомобіля BMW,

· чи скористався клієнт розширеною гарантією.

Файл даних для аналізу методом найближчих сусідів за допомогою пакету WEKA

@attribute IncomeBracket {0,1,2,3,4,5,6,7}@attribute FirstPurchase numeric@attribute LastPurchase numeric@attribute responded {1,0} @data 4,200210,200601,05,200301,200601,1...