
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Динамическое описание систем.Содержание книги
Поиск на нашем сайте
Данное описание удобно тем, что используется богатый математический аппарат. В данном случае все переменные называются переменными состояния, а пространство, где меняется переменная, называется пространством состояний.
Rn – n-мерное Эвклидово пространство x – переменная состояния и определенная на Rn U – переменная состояния и определенная на Rm y – переменная состояния и определенная на Rr Условия существования единственного решения выполняется в том случае, если переменная управления U(t) принадлежит одному из следующих классов функций: постоянная, кусочно-постоянная, кусочно-непрерывная, кусочно-гладка функция.
Частными случаями динамической системы являются: линейные системы x’=Ax+Bu y =Cx билинейные системы
Y(t)=Cx(t) линейно-аналитическая система: x’(t)=f(x(t))+U(t)g(x(t)) y(t)=Cx(t)
Минусом динамических систем является отсутствие информации о топологии и структуре системы/модели.
Динамические системы можно представлять нелинейными ДУ:
i=1,n
x – внутренняя переменная системы f – внешнее воздействие на систему – смотри нормальную форму Коши
Представление систем с помощью графов Граф G на множестве вершин X и множестве друг U. G(X,U) Uij=(xi,xj), Дуга Uj исходя из xi и заходит в xj. Такая дуга становится инцидентной вершинам xi и xj. Если взять две вершины Если записано x≤y следовательно x=y или из вершины x в y существует путь. Дуги называются смежными, если они различны, но имеют 1 общую вершину. Вершины смежные, если они различны и существует дуга из одной вершины в другую.
Некая вершина
Вершина
Для неориентированного графа вводится понятие: локальная степень вершины X – число ребер инцидентных вершине x. Обозначается: Если Граф называется однородным степени n, если локальная степень всех вершин
Для ориентированного графа: множество дуг, исходящих из вершины xi записывается
Ориентированный граф называется однородным, если все локальные степени имеют одно и тоже значение:
Если Если Если Неориентированный граф является связанным, если любые xi, xj можно соединить цепью, следовательно для ориентированного графа вводятся понятия сильно связанного графа.
Граф сильно связан, если любые xi, xj существуют из xi в xj.
Способы представления графов 1. Матрица смежности
Для неориентированного графа симметрична. Ее вид зависит от выбора алгебраической нумерации вершин. Для ориентированного их можно подобрать так, что матрица будет треугольной. Свойства матрицы смежности для ориентированного графа: 1) каждый нулевой столбец соответствует источнику 2) каждая нулевая строка – строку 3) если все элементы главной диагонали равны 0, то в графе нет петель 4) появление единицы для любого xi,j. i=j соответствует петле 5) матрица не симметрична 2. Матрица инцидентности В
в Ребра должны быть пронумерованы!
3. Матрица изоморфности В строках через запятую представлены номера входных дуг с плюсом и номера с выходом с минусом. Пример:
Структурный анализ системы Структура – совокупность элементов системы и связей между ними. Модель структуры системы должна отображать отношение элементов как между собой, так и с внешней средой. Система часто является многоуровневой:
Общее задание структуры анализа состоит в том, что исходя из заданного описания элементов системы и связей между ними получают некоторое представление о свойствах системы в целом и о свойствах ее подсистемы. Различают 3 уровня описания связей между элементами в системе: 1) определяет наличие связей в системе 2) изучение направленности связей 3) изучение вида и направления сигналов, определяющих взаимодействие между элементами С помощью графов 1. Неориентированные графы системы, где вершины – это элементы, ребра – связи между элементами. На этом этапе возникают следующие задачи: a) определение целостности системы(связности). Если система не связана, то выделение изолированных подсистем b) выделение циклов c) определение минимальной и максимальной последовательности элементов, которые соответствует заданной задаче. 2. Ориентированный граф, где направление дуг соответствует направлению связей. Основные задачи: a) определение связности системы b) топологическая декомпозиция системы с выделением сильно связанных подсистем c) перечисление входных и выходных полюсов, определение углов, приема выдачи информации d) определение уровней в структуре и определение их взаимосвязей e) определение минимальных и максимальных путей f) определение топологических характеристик значимости элементов g) получение информации о слабых местах структуры 3. Раскрывается состав и характер сигналов взаимосвязей элементов между собой и с внешней средой. Наиболее простой способ определения путей и контуров в системе – матрично-алгоритмический. Они строятся путем последовательного взаимодействия в степень матрицы смежности. «1» в матрице смежности А говорит о наличии путей между i-той и j-той вершинами длины пути = 1. Если возвести матрицу А в квадрат, то наличие единиц в позиции i,j означает путь между этими вершинами длиной 2.
Элемент i,j определяет число путей длиной к от i к j. Таким образом можно определить вершины входящие в контур и его дину. Но для определения конкретного вида контура необходим дополнительный алгоритм. «–» низкое быстродействие «+» просто и наглядно
Порядковая функция на графе Пусть дан граф без контура, тогда порядковая функция будет отображением разбиения всех вершин графа на не пересекаемые подмножества, которые упорядочены таким образом, что если вершина входит в подмножество с номером больше i. Полученные в результате разложения подмножества носят название уровней системы.
|
||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 690; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.148.115.187 (0.009 с.) |






 – это для перехода от векторной формы к матричным преобразованиям.
– это для перехода от векторной формы к матричным преобразованиям.  – матрица Якоби.
– матрица Якоби.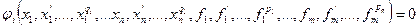



 , и x<y, то вершина Х предшествует вершине Y, следовательно y следует за x.
, и x<y, то вершина Х предшествует вершине Y, следовательно y следует за x. , которая следует за всеми вершинами подмножества Y множества X называется мажорантой (стоком). Может существовать несколько мажорант.
, которая следует за всеми вершинами подмножества Y множества X называется мажорантой (стоком). Может существовать несколько мажорант.
 четно, то вершина тоже и наоборот.
четно, то вершина тоже и наоборот. для любого
для любого  .
. и называются локальной степенью вершины или полустепень исходящей вершины xi.
и называются локальной степенью вершины или полустепень исходящей вершины xi.
 , для любого
, для любого  , то вершина x является изолированной.
, то вершина x является изолированной. , а
, а  , то эта вершина является входом.
, то эта вершина является входом.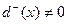 – вершина является выходом.
– вершина является выходом.
 неориентированный
неориентированный ориентированный
ориентированный
 матрица смежности
матрица смежности матрица инцидентности
матрица инцидентности матрица изоморфности
матрица изоморфности
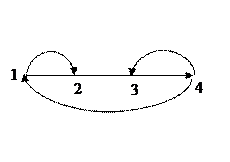
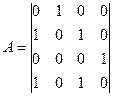
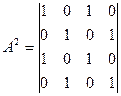
 2-2 разные пути длиной 3
2-2 разные пути длиной 3 2-2 разные пути длиной 4
2-2 разные пути длиной 4


