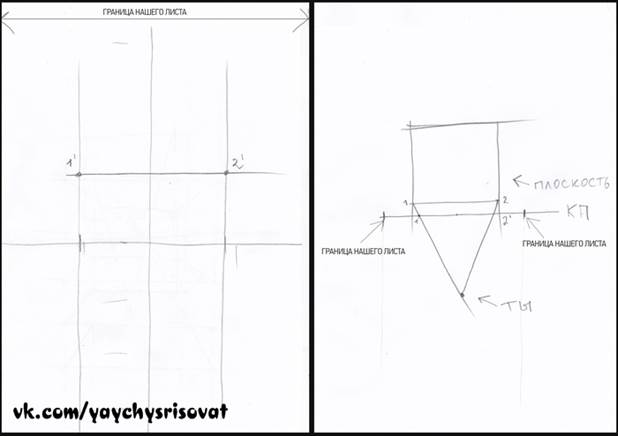
Проецируем переднее ребро плоскости на картинную плоскость

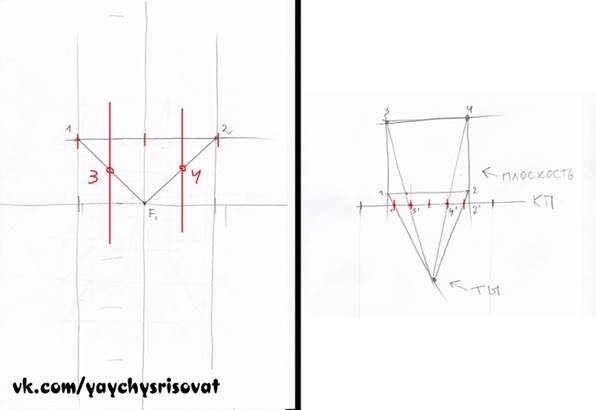
4) Проецируем переднее ребро плоскости на картинную плоскость

 

 

 

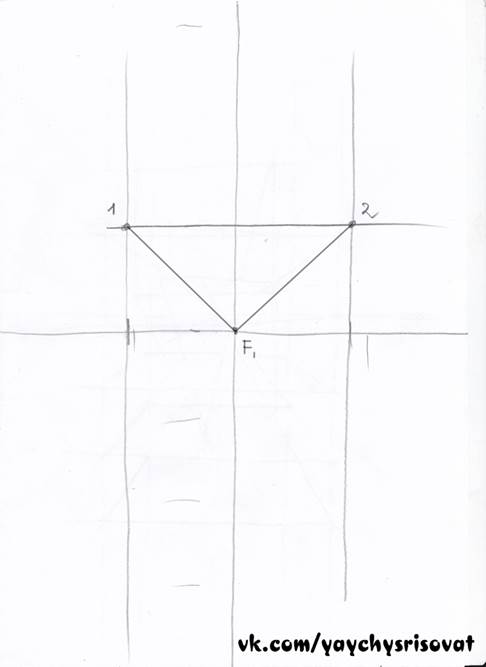
Все просто. Соединяем вершины и получаем пересечения на картинной плоскости. Точки у объекта обозначаем цифрой, а их проекции на картинной плоскости той же цифрой, но уже со штрихом. Соединяем полученные вершины с точкой схода. В результате должно получится следующее

 

 

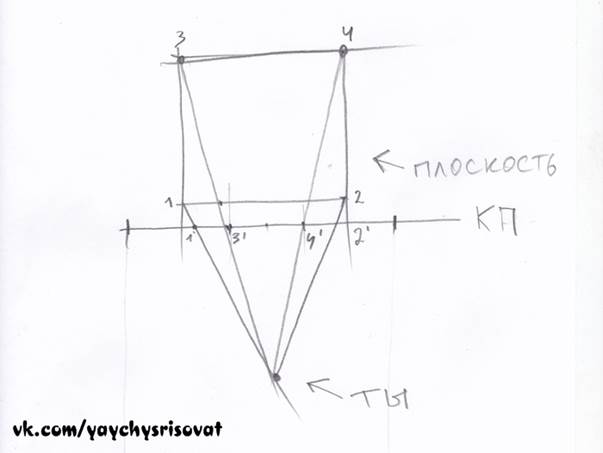
У нас есть переднее ребро плоскости и уходящие в перспективу линии.

5) Проецируем заднее ребро плоскости на картинную плоскость

 

 

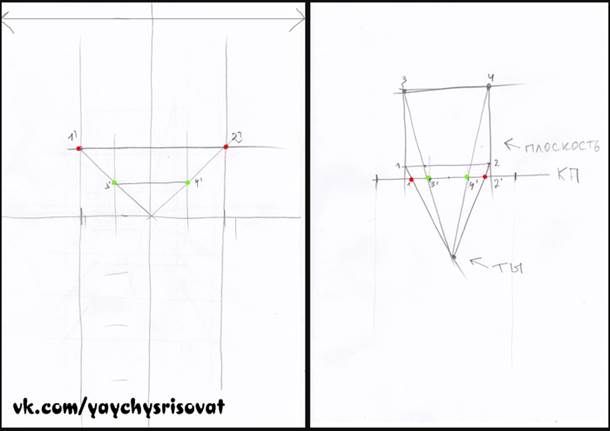
Соединив вершины 3 и 4 c точкой зрения, мы получили точки пересечения на картинной плоскости 3' и 4'.

 

 

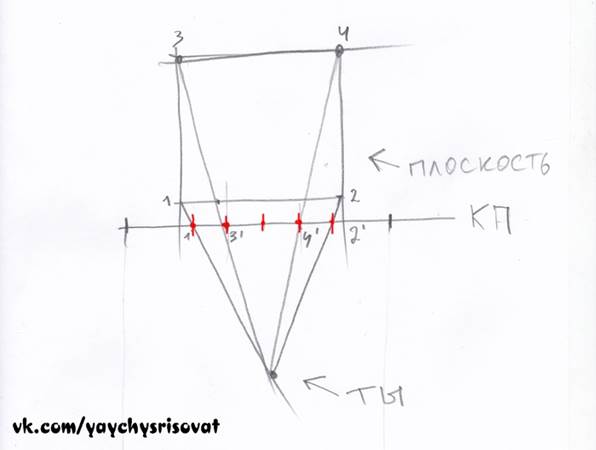
Отмечаем эти точки на проекции. Находим их отношение. Как видим, длина проекции заднего ребра составляет 2/4 от переднего ребра.

 

 

 

Соединив на плане (слева на картинке) вершины 3 и 4 c точкой зрения, мы получили точки пересечения на картинной плоскости 3' и 4'. В результате, должна получится такая фигня

 

 

 

Что ж, на этом остановимся. Для заинтересовавшихся, рекомендую перейти к просмотру ролика, традиционно в конце этого поста) Приятного просмотра.

 

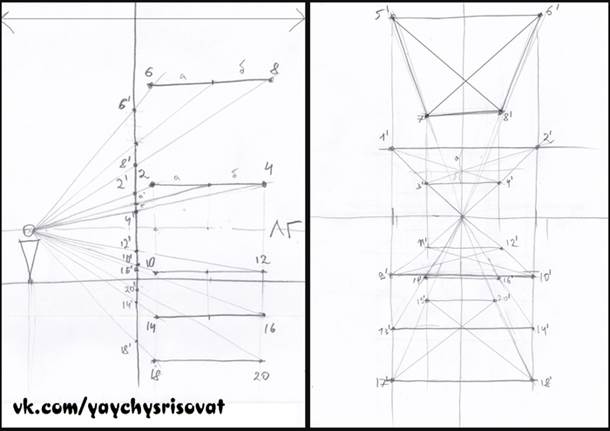
Еще хотел вас домучить объяснениями, почему плоскости сокращаются и их передняя часть больше чем задняя и завершить построение этого упражнения, но, я вовремя осознал, что повествование усложняется, что не вписывается пока в рамки уроков для начинающих.

 

 

ВЫВОД

 

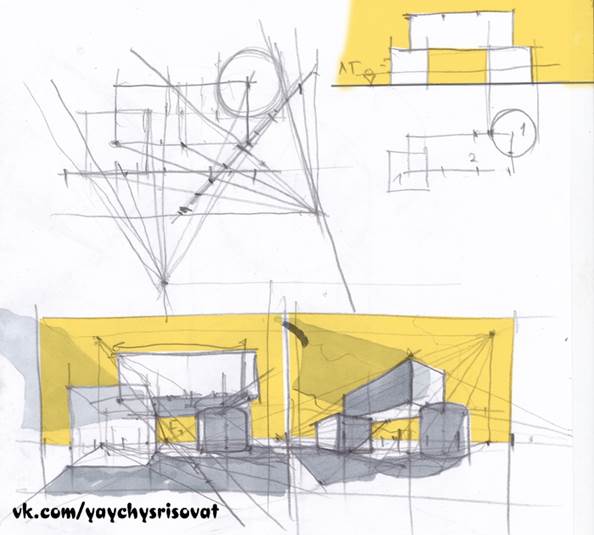
Работа с проекцией на первых порах очень не ясна и непонятна. Однако она дает большие возможности в изображения сложных композиций с разных точек зрения с полным сохранением их взаимного расположения. К примеру, эскиз того, о чем я хочу рассказать в будущем.

 

 

 

Именно умение оперировать объемами фигур в пространстве, отличает архитекторов от художников других дисциплин.

 

Видео: https://youtu.be/FnJniYnTSYY

 

Автор: g4tech