
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгоритмы построения выпуклой оболочки и триангуляцииСодержание книги
Поиск на нашем сайте
Триангуляция Делоне Алгоритм логически делится на два этапа: построение первого тетраэдра и последующий обход с построением остальных тетраэдров разбиения. Опишем первый этап алгоритма – Построение первого тетраэдра. I этап: Построение первого тетраэдра Делоне. Вход: Множество точек N в пространстве. N – количество точек в конечном множестве N. Выход: Первый тетраэдр Делоне (n1,n2,n3,n4).
Рис. 10.6 1. Пусть существует точка внутри выпуклой оболочки множества N, и существуем сколько угодно малая окрестность этой точки, не содержащая точек из N. Такой точкой может быть, например, среднее арифметическое радиус-векторов всех точек N: s= Окрестность точки s не содержит точек множества. Пусть эта окрестность ограничена некой сферой с центром в s. Будем увеличивать эту сферу, так чтобы в итоге на ней лежали четыре и только четыре точки из N, которые и составят первый тетраэдр Делоне.
Рис. 10.7. 2. Сначала включим только одну точку (n1). Начнём расширять сферу, до тех пор, пока она не коснётся одной из точек N. Очевидно, что такой точкой окажется ближайшая к s: n1 Получим сферу с центром в s и радиусом |n1-s|. 3. Будем расширять имеющуюся сферу, пока она не коснётся второй точки из N (n2 Программно этот процесс выглядит как построение для каждой точки из N\{n1} сферы, проходящей через эту точку и n1, центр которой лежит на прямой n1, s, с последующим выбором сферы наименьшего радиуса и соответствующей точки. Построение сферы сводится к вычислению положения центра, который есть точка равноудалённая от всех точек, лежащих на поверхности сферы, кроме того известна прямая, на которой лежит центр. Прямым путём является решение системы из 3-х линейных уравнений (3 неизвестных – координаты центра), и хотя существует множество эффективных алгоритмов решения таких систем, был найден другой способ определения центра сферы. Пусть есть прямая с направляющим вектором v и точка на этой прямой, тогда любую точку прямой можно выразить через сумму радиус вектора исходной точки и вектора t v, где t Итак: a) построим направляющий вектор: v=s-n1; b) определим центр сферы: c=n1+ t v, где t c) для каждой точки ni |ci-n1|=|ci-ni| d) из всех получившихся сфер выберем сферу с наименьшим радиусом: ci=n1+ ti v | ti Получили сферу, центр которой лежит на прямой, перпендикулярной отрезку, соединяющему точки n1 и n2, и проходящей через середину этого отрезка.
Рис. 10.8. 4. Поиск третьей точки происходит аналогично поиску второй. Выберем направляющий вектор, пусть это будет v=c2-m, где m – середина отрезка n1, n2 ((n1+n2)/2), а центр новой сферы определяется как c3=m+t v (Рис. 10.8). Следует заметить, что до текущего шага центр оставался в одной плоскости, а теперь он перейдёт в другую плоскость, которая определяется точками n1, n2 и c2 (непрерывность изменения сферы при этом по-прежнему сохраняется). Снова расширяем сферу, проходящую через точки n1 и n2, сдвигая центр от точки c2 по направлению заданному вектором c2-m и увеличивая радиус, пока сфера не коснётся какой-либо точки из N\{n1,n2}. Формально: a) найдём середину отрезка (n1,n2): m=(n1+n2)/2; b) построим направляющий вектор: v=c2-m; c) центр сферы: c=m + t v, где t d) для каждой точки ni |ci-n1|=|ci-ni|
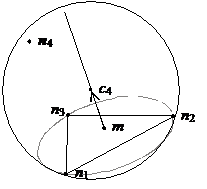
Рис. 10.9. e) из всех получившихся сфер выберем сферу с наименьшим радиусом: ci=m+ ti v | ti 5. Найдём четвёртую точку n4. Три полученных точки составляют треугольник, а описанная вокруг него окружность представляет собой пересечение сферы и плоскости, проходящей через три найденные точки. Центр сферы лежит на прямой, перпендикулярной плоскости полученного треугольника и проходящей через центр описанной вокруг него окружности (Рис. 10.9). Т.о. v=c3-m, где m – центр описанной вокруг треугольника n1,n2,n3 окружности. Будем сдвигать центр сферы из c3 по линии, перпендикулярной плоскости точек n1, n2, n3 и проходящей через центр окружности, описанной вокруг треугольника (n1,n2,n3), увеличивая радиус, так, чтобы точки n1, n2 и n3 продолжали оставаться на сфере. Будем продолжать до тех пор, пока сфера не коснётся какой-либо точки из N\{n1,n2,n3}. Формально: a) найдём центр окружности (m), описанной вокруг треугольника (n1,n2,n3): пусть: m´ – середина отрезка n1, n2; m´=(n1+n2)/2 n´ – вектор нормали плоскости трёх найденных точек v´ – вектор в плоскости треугольника, v´ тогда m=m´+t´ v´ решив уравнение |m´-n1|=|m´-n3|, получим t´. b) построим направляющий вектор: v=c3-m; c) центр сферы: c=m + t v, где t d) для каждой точки ni |ci-n1|=|ci-ni| e) из всех получившихся сфер выберем сферу с наименьшим радиусом: ci=m+ ti v | ti 6. По точкам n1, n2, n3, n4 построим первый тетраэдр Делоне. После выполнения первого этапа алгоритма имеем: тетраэдр, построенный по четырём точкам исходного множества N и удовлетворяющий условию Делоне; новое множество точек в пространстве: N´=N\{n1,n2,n3,n4}. Дальнейший процесс тетраэдеризации сводится к построению тетраэдров на свободных гранях-треугольниках полученной на данном шаге структуры. Для реализации обхода организуется очередь граней, в которую заносятся свободные грани вновь построенных тетраэдров. Треугольник, полученный с верхушки очереди, достраивается до тетраэдра аналогично поиску четвёртой точки в I этапе алгоритма (п. 5).
Рис. 10.10. Различия заключаются лишь в диапазоне возможных значений скаляра t. Рассмотрим эту ситуацию на плоском примере (Рис. 10.10). Имеется уже построенный треугольник и окружность, описанная вокруг него (серый цвет). При построении смежного треугольника используется направляющий вектор построенного треугольника, а именно, разность центра описанной окружности и середины той стороны треугольника, к которой строится смежный треугольник. Центр окружности существующего треугольника делит перпендикулярную к стороне прямую на две полупрямых. Очевидно, что для расположения центра окружности нового треугольника подходит только одна полупрямая, та, которая пересекает сторону треугольника. При этом центр может лежать на полупрямой как с одной, так и с другой стороны, относительно точки пересечения со стороной. Т.о. t Опишем подробно второй этап алгоритма: II этап: Построение полного разбиения на тетраэдры Делоне Вход: Первый тетраэдр (n1,n2,n3,n4), множество точек N´=N\{n1,n2,n3}. Выход: Разбиение на тетраэдры Делоне. 1. Определим B – множество элементов [o, p, r, h] (очередь граней), где o, p, r 2. Инициализируем B гранями первого тетраэдра: B={[n1, n2, n3, h1], [n1, n2, n4, h2], [n2, n3, n4, h3], [n3, n1, n4, h4]}.
Рис. 10.11. 3. Вычтем элемент из B, для которого найдём четвёртую точку q, т.к. три точки мы уже знаем (первые три точки определяет грань уже построенного тетраэдра). Будем двигать центр сферы по линии, перпендикулярной плоскости известной грани и проходящей через центр окружности, описанной вокруг треугольника-грани, увеличивая радиус, так, чтобы известные точки грани продолжали оставаться на сфере (Рис. 10.11). Будем расширять сферу до тех пор, пока она не коснётся какой-либо точки из N´. Формально: a) возьмём элемент из B [o, p, r, h] (точки o, p, r определяют грань тетраэдра, а h является вектором нормали этой грани); b) найдём центр окружности (m), описанной вокруг треугольника (o,p,r): пусть: m´ – середина отрезка o, p; m´=(o+p)/2 v´ – вектор в плоскости треугольника, v´ тогда m=m´+t´ v´ решив уравнение |m´-o|=|m´-r|, получим t´. c) центр сферы: c=m + t h, где t d) для каждой точки ni |ci-o|=|ci-ni| e) из всех получившихся сфер выберем сферу, которой соответствует максимальное t: ci=m+ ti h | ti f) если ни одного ti не найдено, то грань (o,p,r) является внешней гранью множества. 4. По точкам o, p, r, q построим очередной тетраэдр Делоне. 5. Добавим к B три грани очередного тетраэдра, содержащие точку q, причём, если добавляемая грань уже принадлежит B, то вместо добавления удаляем существующую. Такое действие соответствует операции исключающего или (xor). Итак: B=B xor {[o, p, q, g2], [p, r, q, g3], [r, o, q, g4]}, где g2, g3, g4 – вектора-нормали плоскостей соответствующих граней, направленные внутрь тетраэдра. 6. Если B не пусто, то вернёмся к п. 3. Ячейки Вороного Ячейки Вороного строятся только для внутренних точек множества (т.е. для точек не лежащих на оболочке множества). Значит нужно выделить такие точки и построить вокруг каждой ячейку Вороного. Затем полученные ячейки объединяются в единую структуру. Опишем построение отдельной ячейки Вороного: I этап: поиск вершин ячейки Вороного Вход: По аналогии с двумерным случаем, вершинами ячейки являются центры описанных вокруг тетраэдров Делоне сфер. Для расчёта этих центров берутся тетраэдры, содержащие точку, вокруг которой строится ячейка (далее: точка p). 1. Создадим очередь B, элементами которой будут указатели на грани тетраэдров. 2. Возьмём какой-либо тетраэдр, содержащий точку p. Вычислив центр описанной сферы, занесём его в массив вершин ячейки. Добавим к B три грани этого тетраэдра, содержащие p. Пометим тетраэдр. 3. Берём элемент с верхушки очереди: b=first(B). 4. Если грань b принадлежит не помеченному тетраэдру, то переходим по грани b к следующему тетраэдру. 5. Вычислив центр описанной вокруг него сферы, занесём его в массив вершин ячейки. Добавим к B две грани (три грани содержат точку, а та из них, по которой перешли к данному тетраэдру, уже обработана) этого тетраэдра, содержащие p. Пометим тетраэдр. 6. Если очередь B не пуста, то перейти к (3). Получим массив вершин ячейки. Т.о. задача сводится к построению выпуклой оболочки множества точек. Алгоритм использует метод «заворачивания подарка», который заключается в последовательном обходе точек множества, лежащих на его границе. 1. Пусть одна грань оболочки (грань f0) уже известна. 2. Создадим очередь Q, содержащую ребра оболочки. 3. Занесём в Q грани f0. 4. Берём элемент с верхушки очереди: q=first(Q). 5. f – грань, к которой принадлежит q. 6. Найдём точку p из множества, такую, что плоскость, проходящая через q и эту точку, образует с f максимальный угол < 7. Построим новую грань на q и p. Занесём её рёбра в Q, кроме q, и тех, которые не смыкаются с другими гранями. 8. Если очередь Q не пуста, то перейти к (4). Получим выпуклую оболочку, которая и будет являться ячейкой Вороного. 10.6 Вопросы и упражнения 1. Дайте определение триангуляции Делоне. 2. Сформулируйте задачу построения триангуляции в пространстве. 3. Привести пример неоднозначной триангуляции Делоне. 4. Дайте определение диаграммы Вороного. 5. Для каких центров из конечной системы точек, для которой строится диаграмма Вороного, их ячейка Вороного бесконечна. 6. В чем состоит дуальность разбиений Делоне и Вороного? 7. Адаптировать алгоритм построения триангуляции Делоне методом вкатывания «пустого» шара в пространстве к подобной задаче на плоскости. 8. Сколько минимально ячеек в диаграмме Вороного на плоскости и в пространстве может сходиться в одной точке?
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 7; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.130.127 (0.01 с.) |


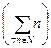 / |N|
/ |N|
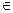 N | |n1-s|=
N | |n1-s|= 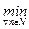 (|n-s|)
(|n-s|)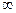 ) (в силу непрерывности). Т.о. центр сферы для второй точки можно задать: c2=n1+ t v, остаётся выбрать сферу с минимальным радиусом. Нетрудно заметить, что радиус принимает минимальное значение при минимальном значении t. Значение t для заданной точки ni из N\{n1} вычисляется путём решения линейного уравнения: |c2-n1| = |c2-ni|
) (в силу непрерывности). Т.о. центр сферы для второй точки можно задать: c2=n1+ t v, остаётся выбрать сферу с минимальным радиусом. Нетрудно заметить, что радиус принимает минимальное значение при минимальном значении t. Значение t для заданной точки ni из N\{n1} вычисляется путём решения линейного уравнения: |c2-n1| = |c2-ni|  |t v| = |n1+ t v-ni|.
|t v| = |n1+ t v-ni|. min
min 
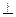 (n1-n2); v´=(n1-n2)
(n1-n2); v´=(n1-n2) 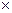 n´
n´
 .
.


