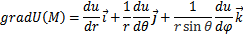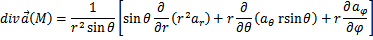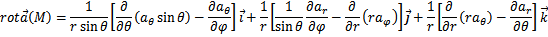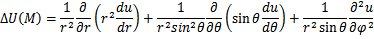Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
e1,e2,e3-единичные, e1*e1=e2*e2=e3*e3=1Содержание книги
Поиск на нашем сайте
в) Выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи коэффициентов Ламе.
г) Запишите основные дифференциальные операции в криволинейных координатах.
2. Решение дифференциальных уравнений в частных производных методом функции Грина. (35 баллов) а) Что такое дифференциальное уравнение в частных производных? Дифференциальное уравнение в частных производных— дифференциальное уравнение, содержащее неизвестные функции нескольких переменных и их частные производные. б) В чем заключается метод функции Грина? Фу́нкция Гри́на используется для решения неоднородных дифференциальных уравнений с граничными условиями (неоднородной краевой задачи). Они помогают находить стационарные и нестационарные решения, в том числе при разнообразных граничных условиях. в) Приведите пример. Пусть многообразие задаётся первой четвертью плоскости (x,y) : x,y≥0 L- оператор Лапласа. Также предположим, что при х=0 наложены краевые условия Дирихле, при у=0 краевые условия Неймана. Тогда функция Грина примет вид
11)1. Цилиндрическая система координат. (35 баллов) а) Назовите цилиндрические координаты. Покажите связь цилиндрических и декартовых координат. (1)Цилиндрической системой координат называют трёхмерную систему координат, являющуюся расширением полярной системы координат путём добавления третьей координаты(обычно обозначаемой z) которая задаёт высоту точку над плоскостью. Цилиндрические координаты точки состоит из упорядоченной тройкой (
б) Назовите координатные поверхности и координатные линии в цилиндрической системе координат. Координатными поверхностями в цил.сис.коордат явл.: в) Определите коэффициенты Ламе в цилиндрической системе координат и выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи этих коэффициентов Ламе.
г) Запишите основные дифференциальные операции в цилиндрических координатах.
2. Определите потенциал электростатического поля методом функции Грина. (35 баллов) а) Запишите уравнение Пуассона для потенциала электростатического поля. Уравнение Пуассона для потенциала электростатического поля:
б) Сформулируйте граничное условие для данной задачи. в) Примените метод функции Грина для определения потенциала электростатического поля. 12) 1. Сферическая система координат. (35 баллов) а) Назовите сферические координаты. Покажите связь сферических и декартовых координат. Сферическими координатами наз. систему координат для отображения геометрических свойств фигуры в трёх измерениях посредством задания трёх координат-( б) Назовите координатные поверхности и координатные линии в сферической системе координат. Координатные поверхности в сферической системе координат являются:r=const-сферы с центрами в точке 0; в) Определите коэффициенты Ламе в сферической системе координат и выразите элементы длин дуг соответствующих координатных линий, элементы площадей координатных поверхностей и элемент объема при помощи этих коэффициентов Ламе. Линии (
г) Запишите основные дифференциальные операции в сферических координатах.
2. Уравнения гиперболического типа и метод их решения. (35 баллов)
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.2.242 (0.006 с.) |

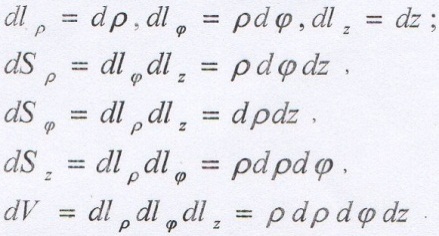
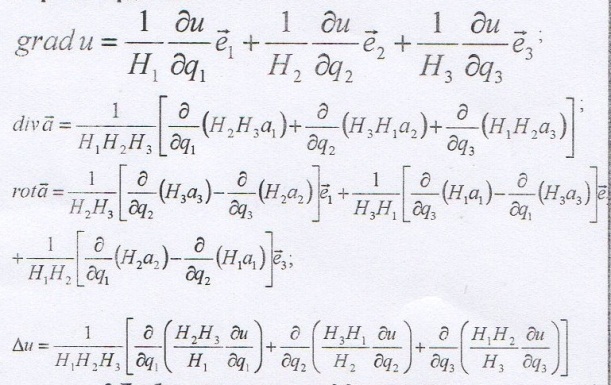
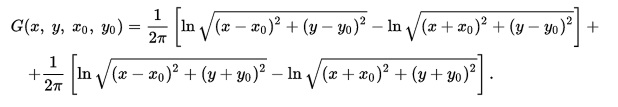
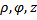 ) а также (x,y,z). Орты цилиндрической системы координат связаны с декартовыми ортами следующими соотношениями:
) а также (x,y,z). Орты цилиндрической системы координат связаны с декартовыми ортами следующими соотношениями: 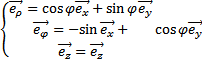 , и образует правую тройку:
, и образует правую тройку: 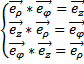 , обратные соотношения имеют вид
, обратные соотношения имеют вид 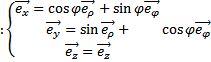 , закон преобразования координат от цилиндрических к декартовым:
, закон преобразования координат от цилиндрических к декартовым: 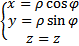 , закон преобразования координат от декартовым к цилиндрических:
, закон преобразования координат от декартовым к цилиндрических: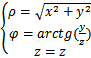 Якобиан равен: J=
Якобиан равен: J= 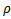
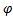 =const-полуплоскости, ограниченные осью 0z;
=const-полуплоскости, ограниченные осью 0z;  =const-плоскости,
=const-плоскости,  к осью 0z. Коэф-ты Ламе в цил.сис.коордат имеют вид:
к осью 0z. Коэф-ты Ламе в цил.сис.коордат имеют вид: 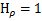 ;
; 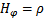 ;
; 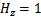 . Их элементы:
. Их элементы: 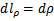 ,
, 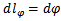 ,
, 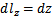 ;
; 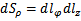 =
= 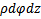 ,
, 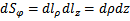 ,
, 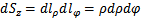 ,
, 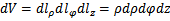 Пересечение двух коорд. поверхностей явл. коорд. линиями.
Пересечение двух коорд. поверхностей явл. коорд. линиями.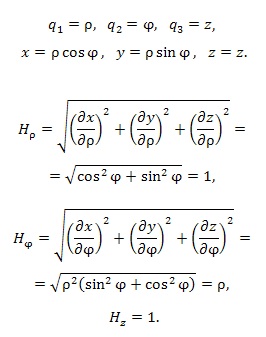
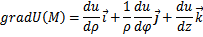
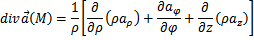
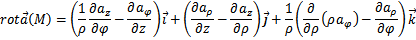
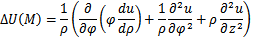
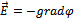 ;
; 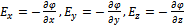 ;
;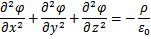
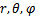 ). Связь между декартовыми и сферическими координатами описывается формулами---
). Связь между декартовыми и сферическими координатами описывается формулами--- 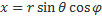 ;
; 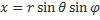 ;
; 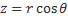 ;
; 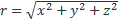 ;
; 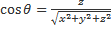 ;
; 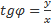 .
.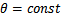 -конусы с осью Oz;
-конусы с осью Oz; 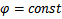 -полуплоскости, ограниченные осью Oz. Координатными линиями будут: (r)=лучи, выходящие из центра 0; линии(
-полуплоскости, ограниченные осью Oz. Координатными линиями будут: (r)=лучи, выходящие из центра 0; линии( 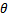 )-окружности с центрами в точке 0 и радиусами r, пересекающие ось Oz;
)-окружности с центрами в точке 0 и радиусами r, пересекающие ось Oz;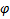 )-окружности с центрами на оси Oz и радиусами MM3=
)-окружности с центрами на оси Oz и радиусами MM3= 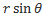 . Коэффициенты Ламе в сферической системе координат
. Коэффициенты Ламе в сферической системе координат 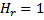 ;
; 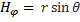 ;
; 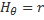 . Элементы:
. Элементы:  ;
; 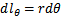 ;
; 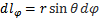 ;
; 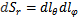 =
= 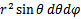 ;
; 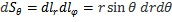 ;
; 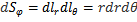 ;
; 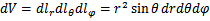 .
.