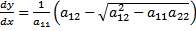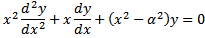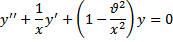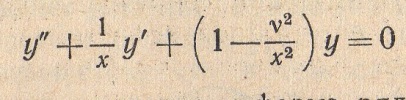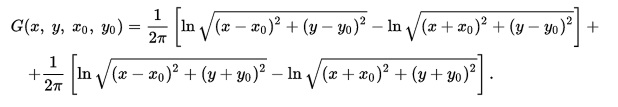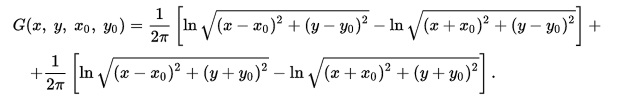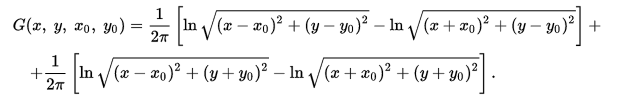Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения эллиптического типа и метод их решенияСодержание книги
Поиск на нашем сайте
уравнение Шрендингера
б) Какие существуют методы решения уравнений параболического типа? (задача Коши для параболического уравнения) используют специальную интегральную формулу, метод разделения переменных Фурье. метод конечных элементов, метод конечных разностей, метод конечных объёмов, а так же их комбинации и другие численные методы, в) С помощью одного из методов решить уравнение данного типа.
14) 1. Скалярные, векторные и тензорные величины. (35 баллов) а) Что такое скалярная величина? Скалярная величина это величина, каждое значение которой может быть выражено одним действительным числом. То есть скалярная величина определяется только значением, в отличие от вектора, который кроме значения имеет направление. К скалярным величинам относятся длина, площадь, время, температура и т. д. б) Что такое векторная величина? Векторная величина это физическая величина, являющаяся вектором. Противопоставляется с одной стороны скалярным с другой — тензорным величинам. Также может противопоставляться тем или иным объектам совершенно другой математической природы. в) Что такое тензор? Тензор это объект линейной алгебры, линейно преобразующий элементы одного линейного пространства в элементы другого. Частными случаями тензоров являются скаляры, векторы, билинейные формы и т. п. Термин «тензор» также часто служит сокращением для термина «тензорное поле», изучением которых занимается тензорное исчисление.
2. Уравнения эллиптического типа и метод их решения. (35 баллов) а) Назовите физические задачи, описываемые уравнениями эллиптического типа. Физические задачи, описываемые уравнениями эллиптического типа это ур.Пуассона, ур.Лапласа, стационарное ур.Шредингера. Для решения уравнения эллиптического типа применяются различные типы методов. Один из расппрастраненных методов это метод функции Грина. Оно состоит в том что сначало находят некоторые специальные решение задачи такого же типа, а затем через него в квадратурах выражают интеграл исходный задач.
в) С помощью одного из методов решить уравнение данного типа.
15)1. Векторные линии. (35 баллов) Векторной линией называется такая линия векторного поля, в каждой точке которой вектор ноля касается линии. Понятие о векторной линии возникает как обобщение линии тока в стационарном потоке жидкости, т. е. линии, но которой движется частица жидкости такого потока. Хорошо известными примерами векторных линий являются также силовые линии магнитного и электрического полей. Для геометрической характеристики векторного поля служат векторные линии. В силовом поле векторные линии называется силовыми линиями, в поле скоростей движения жидкости векторные линии называется линиями тока.
2. Приведение дифференциальных уравнений в частных производных к каноническому виду. (35 баллов) Уравнение связывающии искомую функцию, нез.перменами в част.произ.по этим переменным от искомый функции наз.дифф.урав.в частных произ. Порядком диф.уравнения называется порядок старшии производной, входящей в это уравнения.
В зависимости от соотн.между коэф-ми при старших производных ур.в част.произ.делятся на 3 типа: 1) если Для того чтобы привести к каноническому виду надо состовит его характерическое уравнения: 16) 1. Основные задачи математической физики. (35 баллов) Основная задача математической физики являются аналитическая исследования сука скалярных, векторных и тензорных полей физических величин. Математическая физика – теория математических моделей физических явлений; занимает особое положение и в математике, и в физике, находясь на стыке этих наук. Математическая физика тесно связана с физикой в той части, которая касается построения математической модели, и в то же время математическая физика - раздел математики, поскольку методы исследования моделей являются математическими. В понятие методов математической физики включаются те математические методы, которые применяются для построения и изучения математических моделей, описывающих большие классы физических явлений. В мат.физике расс. 2 задачи(пролемы): 1.Прямая-заданные поле требуется установить характер этого поля. Этим занимается-мат.теория поля. 2.Обратное-опр.конкретного вида мат.поля, если известно условия в который находится физ.объект. Эту проблему решает теория дифф.урав.в.част.произ. Решение уравнения Бесселя
Цилиндрические функции - Функции Бесселя, Функции Ганкеля, Функция Бурже, Модифицированные функции Бесселя, Функции параболического цилиндра, Функции Кельвина
2. Решение уравнения Бесселя. (35 баллов) а) Напишите уравнение Бесселя.
В)
в) Назовите цилиндрические функции. Запишите выражения для цилиндрических функций.
{\displaystyle (r,\varphi ,z).}() {\displaystyle (r,\varphi ,z).}()
|
||||
|
Последнее изменение этой страницы: 2024-06-27; просмотров: 7; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.2.242 (0.007 с.) |

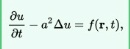 Уравнение теплопроводности
Уравнение теплопроводности

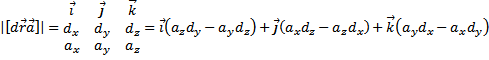
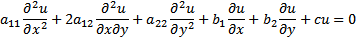
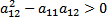 , то уравнения будет гиперюболического типа; 2) если
, то уравнения будет гиперюболического типа; 2) если 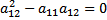 , то это будет ур.параболического типа; 3) если
, то это будет ур.параболического типа; 3) если 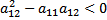 , а это ур.эллиптического типа.
, а это ур.эллиптического типа.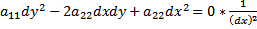 ;
; 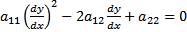 ;
; 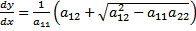 ;
;