Генерация решений с помощью экспертных систем

3.2. Постановка задачи

 Постановка конкретной задачи принятия решений (ЗПР) включает:

- формулировку задачи;

- определение типа задачи;

- выбор метода решения;

- определение множества альтернатив и основных критериев для выбора из них наилучшей и согласование критериев.

Для решения задач широко применяются различные методы.

3.2.1. Математическое моделирование при принятии решений

При построении, изучении и применении экономико-математических моделей принятия решений используются различные математические методы, именуемые экономико-математическими. Их можно разделить на несколько групп:

- методы оптимизации;

- методы, учитывающие неопределенность, прежде всего вероятностно-статистические;

- методы построения и анализа имитационных моделей;

- методы анализа конфликтных ситуаций (теории игр).

Во всех этих группах можно выделить статическую и динамическую постановки. При наличии фактора времени используют дифференциальные уравнения и разностные методы.

Математическое программирование – это семейство инструментальных средств, созданных для помощи в процессе решения управленческих задач, при котором лицо, принимающее решения, должно выделить ограниченные ресурсы для различных действий или операций с условием оптимизации измеримой цели. Наиболее известным методом этого семейства инструментов является линейное программирование. Оно широко используется в информационных системах поддержки руководителя (ИСПР) и имеет много важных практических приложений, например решение задачи распределения (ресурсов или времени).

Задачи распределения, решаемые на основе линейного программирования, обычно отражают следующие характеристики:

- для распределения доступно ограниченное количество ресурсов;

- ресурсы используются в производстве продукции или услуг;

- существует два или более путей использования ресурсов, каждый из которых называется решением или программой;

- распределение обычно ограничивается несколькими доступными пределами и требованиями, называемыми ограничениями.

Модель распределения линейного программирования основывается на следующих различных экономических допущениях:

- отдача или доходность при различных вариантах распределения могут сравниваться, т.е. они могут быть измерены в общих единицах
(например, денежных);

 

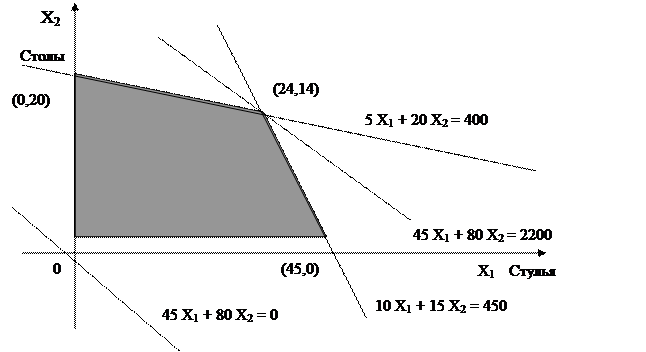
- отдача от одного распределения независима от других распределений;

- общая доходность является суммой доходностей, принесенных различными действиями;

- все исходные данные известны и определены.

Наиболее известны задачи линейного программирования, в которых максимизируемая функция F(X) является линейной, а ограничения А задаются линейными неравенствами.

Пример [4].Цех может производить стулья и столы. На производство стула идет 5 единиц материала, на производство стола – 20 (футов красного дерева). Трудоемкость изготовления одного стула 10 человеко-часов, стола – 15. Имеется 400 единиц материала и 450 человеко-часов. Прибыль при производстве стула – 45 долларов США, при производстве стола −
80 долларов США. Сколько надо сделать стульев и столов, чтобы получить максимальную прибыль?

Введем обозначения: Х₁ – число изготовленных стульев;

Х₂ – число сделанных столов. Задача оптимизации имеет вид:

45 Х₁ + 80 Х₂  → max;

5 Х₁ + 20 Х₂ ≤ 400;

10 Х₁ + 15 Х₂ ≤ 450;

Х₁  ≥ 0;

Х₂ ≥ 0.

В первой строке выписана целевая функция − прибыль при выпуске Х₁ стульев и Х₂ столов. Ее требуется максимизировать, выбирая оптимальные значения переменных Х₁ и Х₂ . При этом должны быть выполнены ограничения по материалу (вторая строчка) − может быть истрачено не более 400 футов красного дерева, а также и ограничения по труду (третья строчка) − работы выполнялись в течение 450 часов. Кроме того, нельзя забывать, что числа столов и  стульев положительны.

В четвертой и пятой строчках задачи и констатируется, что переменные неотрицательны.

 Условия производственной задачи можно изобразить на координатной плоскости. По горизонтальной оси абсцисс будем откладывать значения Х₁ , а по вертикальной оси ординат − значения Х₂ .

   Рис. 4. Основная идея линейного программирования

 

  

 

Таким образом, множество возможных значений объемов выпуска стульев и столов (Х₁, Х₂) представляет собой выпуклый четырехугольник, показанный на рисунке 4. Три его вершины очевидны − это (0,0), (45,0) и (0,20). Четвертая − это пересечение двух прямых, т. е. решение системы уравнений следующее:      

                       5Х₁ + 20Х₂ = 400;

                       10Х₁ + 15Х₂ = 450.

Из первого уравнения: 5Х₁ = 400 − 20Х₂; Х₁ = 80 − 4Х₂ . Подставляем во второе уравнение: 10(80 − 4Х₂) + 15Х₂ = 800 − 40Х₂ + 15Х₂ =
= 800 − 25Х₂ = 450, следовательно, 25Х₂ = 350, Х₂ = 14. Отсюда
Х₁ = 80 − 4×14 = 80 − 56 = 24. Итак, четвертая вершина четырехугольника − это (24, 14).

Основная идея линейного программирования состоит в том, что максимум достигается в вершинах многоугольника. Максимум целевой функции, равный 2200, достигается в вершине (24, 14).

Таким образом, оптимальный выпуск таков: 24 стула и 14 столов. При этом используется весь материал и все трудовые ресурсы, а прибыль равна 2200 долларам США.

При решении ЗПР часто возникают проблемы, которые по различным причинам не могут быть формализованы и решены с применением разработанного в настоящее время математического аппарата. В этих случаях прибегают к услугам экспертов (системных аналитиков), чей опыт и интуиция помогают упростить проблему.

На работу эксперта оказывают влияние следующие факторы:

 – ответственность за использование результатов экспертизы;

 – знание того, что привлекаются и другие эксперты;

 – наличие информационного контакта между экспертами;

 – межличностные отношения экспертов (если между ними есть информационный контакт);

 – личная заинтересованность эксперта в результатах оценки;

 – личностные качества экспертов (самолюбие, конформизм, и др.).

Существуют различные методы математической обработки мнений экспертов. Экспертам предлагают оценить различные альтернативы либо одним, либо системой показателей. Кроме того, им предлагают оценить степень важности каждого показателя (его «вес» или «вклад»). Самим экспертам также приписывается уровень компетентности, соответствующий вкладу эксперта в результирующее мнение группы.

Экспертная система, используя знания, получен­ные от специалистов в данной предметной области, решает те же проблемы, экспертами в которых являются эти же специалисты, но только с применением компьютера.

Необходимо особо подчеркнуть, что существует принципиальное различие в характере использования экспертных методов в экспертных системах и в поддержке принятия решений. Если в первом случае от экспертов требуется формализация способов принятия решений, то во втором  – лишь само решение как таковое.