Выражение скалярного произведения через координаты векторов

27. Выражение скалярного произведения через координаты векторов

Теорема: Скалярное произведение двух векторов равно сумме попарных произведений соответствующих координат этих векторов

1) (a,b)=X₁X₂в R¹

2) (a,b)=X₁X₂ + Y₁Y₂ в R²

3) (a,b)=X₁X₂ + Y₁Y₂ + Z₁Z₂в R³

 

28. Прямая линия на плоскости

1) y=kx+b – уравнение прямой с угловым коэффициентом (k=tgα, α – угол наклона прямой к Ох)

2) Уравнениепрямой проходящей через тоску М₀ (х₀;у₀) с k: у-у₀=k(х-х₀)

3) Уравнение прямой проходящей через 2 точки А(х₁:у₁) и В(х₂;у₂)

 

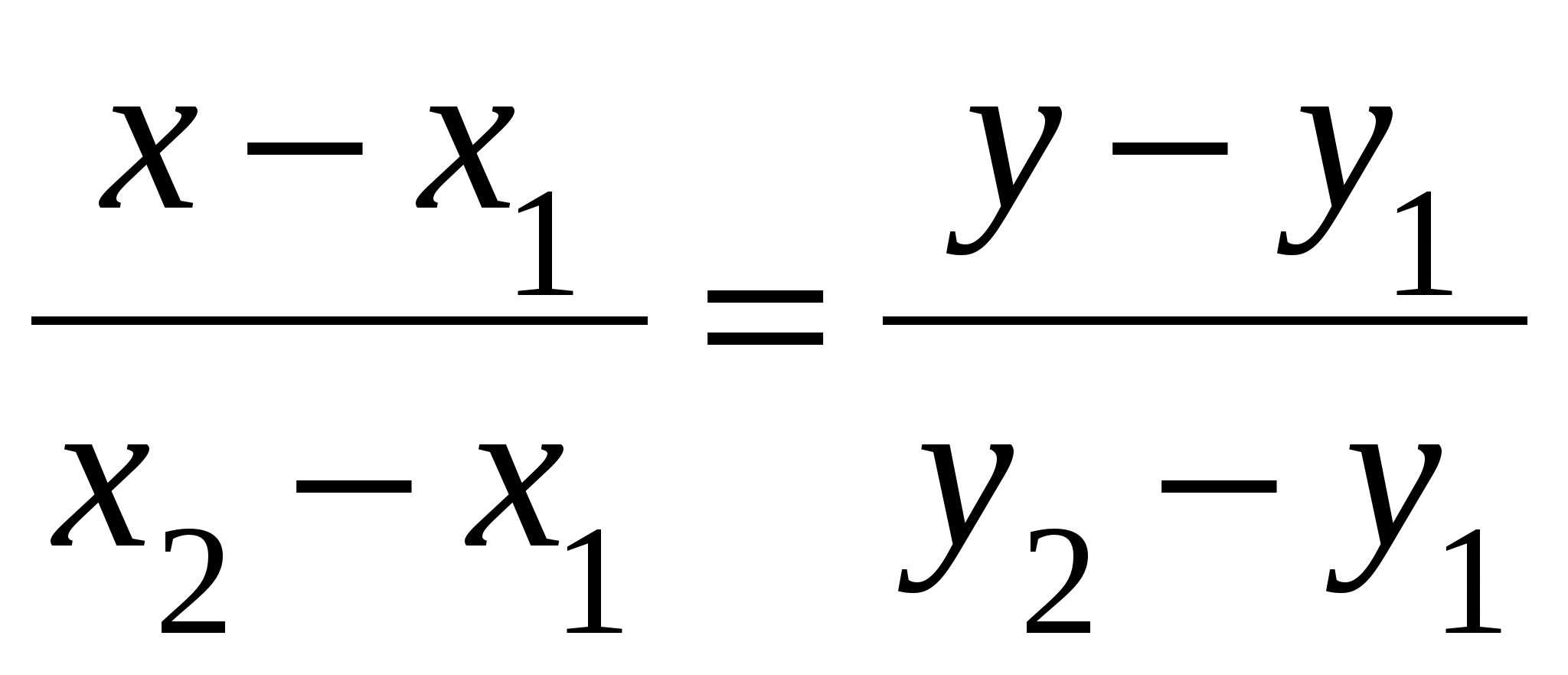
4) Уравнение прямой в отрезках

 

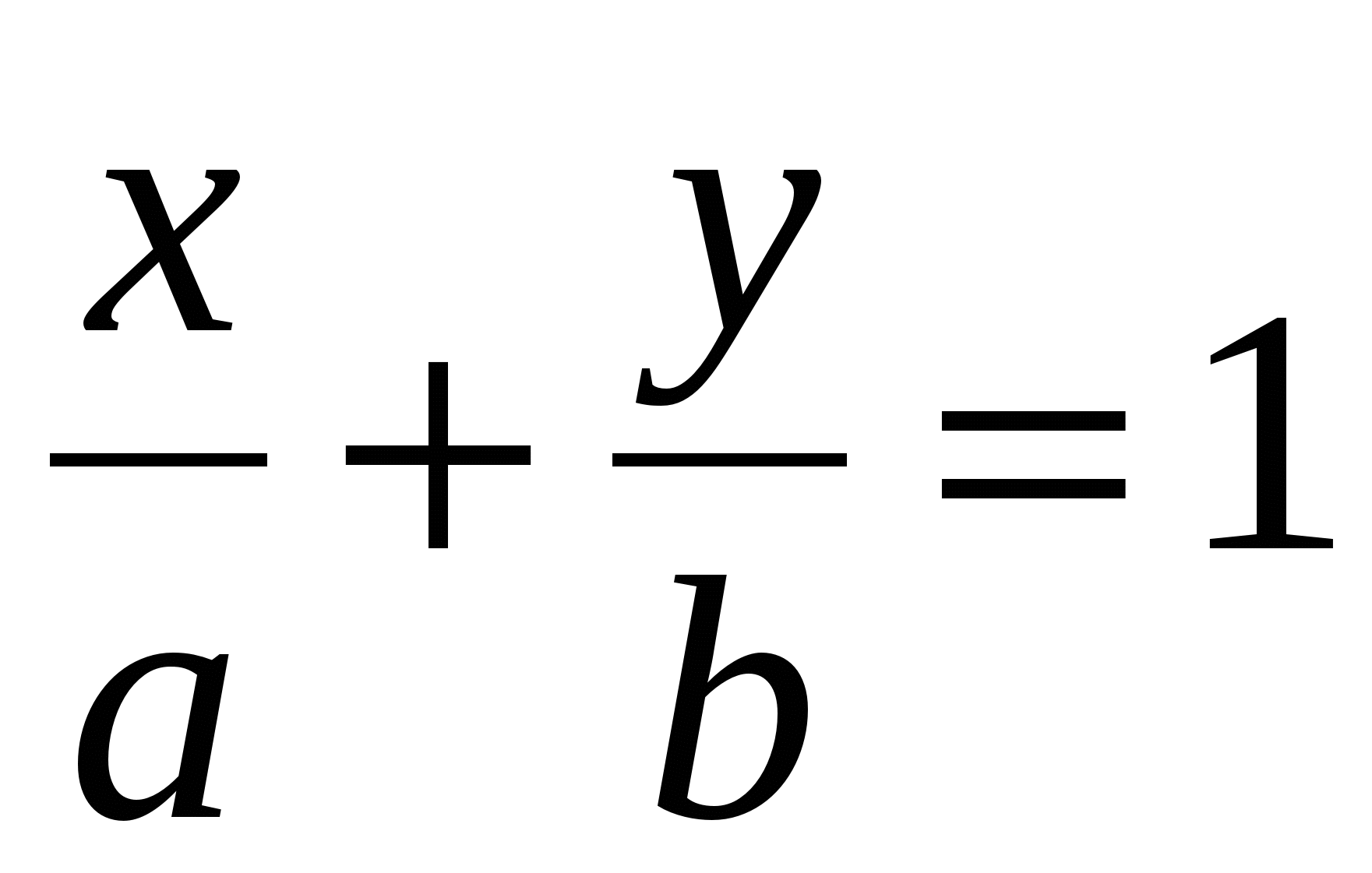
5) Общее уравнение прямой

Ах + Ву + С = 0

1. С=0

Ах + Ву = 0 (прямая через (0;0))

2. А=0, В и С≠0

Ву + С = 0 (прямая || Ох)

3. В=0, А и С≠0

Ах + С = 0 (прямая ||Оу)

 

29. Взаимное расположение прямых линий на плоскости

1) r(Q)=r(Q)=2, т.е. ранги матриц совпадают и равны 2

Прямые пересекаются. Т.к. ранги матриц Qи Qсовпадают, то система совместна, т.е. имеет решения. А т.к. ранг матрицы системы равен числу неизвестных, то решение системы единственно, прямые пересекаются в одной точке.

2) r(Q)≠r(Q)

Система не имеет решений, следовательно, прямые параллельны

3) r(Q) = r(Q) = 1

т.к. ранги матриц совпадают, то система совместна. А т.к. ранг матрицы системы меньше числа неизвестных, то система имеет бесчисленное множество решений. Следовательно прямые совпадают.

 

30. Окружность и эллипс (канонические уравнения)

Ax² + By² + Cx + Dy + E = 0

1) A=B – задана окружность

(х – х₀)² + (у – у₀)² = R²

(x₀;y₀) – центр окружности

R–радиус

2) А≠В , одинаковый знак – эллипс

 

 

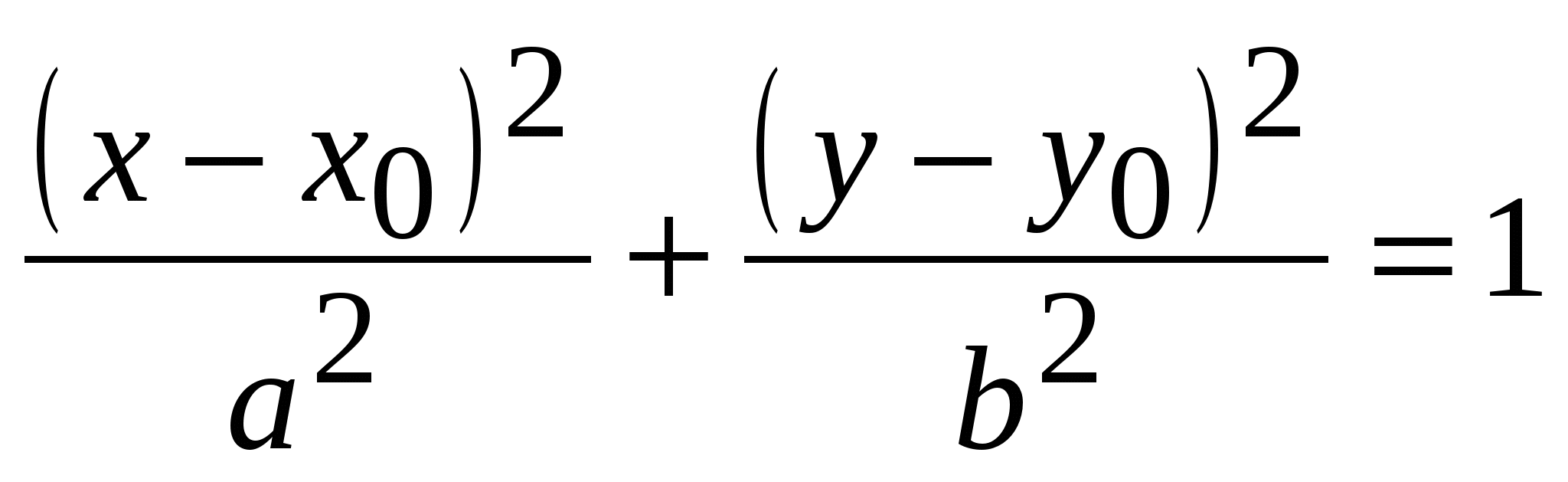
(x₀;y₀) – центр эллипса

а и b– полуоси

a||Ox; b||Oy