
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Описание лабораторной установкиСодержание книги
Поиск на нашем сайте
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ __________________________ Пензенский государственный университет
Изучение вращательного движения Методические указания
Пенза 2003 УДК 531.23 ББК 22я7 И39 Рекомендовано Редсоветом университета
Рецензент – кандидат физико-математических наук, доцент И.Д.Караман
И39
Изучениевращательного движения с помощью маятника Обербека и его компьютерного имитатора: Методические указания к лабораторной работе № 9
Изложены основные положения кинематики и динамики твердого тела. Приведена методика и описан эксперимент по проверке основного закона динамики вращательного движения. Эксперимент может быть выполнен как на реальной лабораторной установке (маятнике Обербека), так и на ее компьютерном имитаторе. Методические указания подготовлены на кафедре физики и предназначены для студентов тех специальностей, учебные планы которых предусматривают изучение курса физики.
© Пензенский государственный университет архитектуры и строительства, 2003 © Г.И.Грейсух, С.А.Степанов, С.В.Голобоков, 2003 Цель работы - проверка основного закона динамики вращательного движения и определение момента инерции маятника Обербека. Приборы и принадлежности: лабораторная установка, включающая маятник Обербека, линейку, набор гирей различной массы, секундомер, штангенциркуль, а также IBM-совместимый персональный компьютер и пакет компьютерных программ, имитирующих работу лабораторной установки.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ При изучении различных видов движения протяженных тел широко используется физическая модель абсолютно твердого тела. В рамках этой модели полагают, что действие сил на тело не приводит к его деформации, а влияет лишь на особенности движения тела. В дальнейшем для краткости такую модель будем называть просто «твердым телом». Чтобы указать положение твердого тела в пространстве, необходимо зафиксировать какие-либо три его точки, не лежащие на одной прямой. Эти три точки описываются девятью координатами, между которыми имеются три соотношения, выражающие постоянство расстояний между точками твердого тела. Следовательно, в общем случае движение твердого тела - это движение с шестью степенями свободы. Простейшими видами движения твердого тела являются поступательное и вращательное движения. Поступательным называется движение, при котором любая прямая, жестко связанная с движущимся телом, остается параллельной своему первоначальному положению. Вращательное движение - это такой вид движения, при котором по крайней мере две точки тела остаются неподвижными. Прямая, проходящая через эти точки, называется осью вращения. Все точки твердого тела, лежащие на оси вращения, неподвижны, другие его точки движутся по окружностям в плоскостях, перпендикулярных оси вращения. Центры этих окружностей лежат на оси вращения. Вращательное движение можно рассматривать как движение с одной степенью свободы, если ввести угловую координату j, т.е. угол между двумя плоскостями, проходящими через ось вращения. Одна из этих плоскостей зафиксирована в пространстве, а вторая - жестко связана с телом. При этом для определенности полагают, что в начальный момент времени эти плоскости совпадают, т.е. j0=0.
Быстроту вращения тела характеризуют угловой скоростью
а быстроту изменения угловой скорости – угловым ускорением
Для того чтобы изменить угловую скорость тела, к нему необходимо приложить вращающий момент – величину, характеризующую вращательный эффект силы F при ее воздействии на твердое тело. Вращающий момент численно равен
где Тело, обладая инертностью, противодействует изменению его скорости. Момент инерции – это мера инертности тела при его вращательном движении. Эта величина зависит от массы, формы и размеров тела, а также от расположения оси вращения. Кроме того, для неоднородных тел момент инерции зависит от того, как распределена плотность вещества по объему тела. Обычно момент инерции различных тел приводят относительно оси, проходящей через центр их инерции. Например, момент инерции однородного стержня относительно оси, проходящей через его центр перпендикулярно оси стержня, определяется формулой
где Если же необходимо рассчитать момент инерции I относительно оси, не проходящей через центр инерции тела, то используют теорему Штейнера, связывающую моменты инерции относительно двух параллельных осей, одна из которых проходит через центр инерции тела:
где
Из формулы (5), в частности, следует, что если тело движется по окружности радиусом
Иногда говорят, что формула (6) определяет момент инерции частицы (материальной точки), движущейся по окружности. Ниже приведены моменты инерции некоторых однородных тел правильной геометрической формы: - сплошного цилиндра относительно продольной оси
- полого цилиндра относительно продольной оси
- шара относительно оси, проходящей через его центр
Часто при расчете момента инерции оказывается полезным использовать его свойство аддитивности: момент инерции составного тела равен сумме моментов инерции его отдельных частей:
В соответствии с законом динамики вращательного движения угловое ускорение тела пропорционально результирующему вращающему моменту всех сил, приложенных к телу, и обратно пропорционально моменту инерции тела, т.е.
Результирующий вращающий момент находится как алгебраическая сумма всех вращающих моментов, приложенных к телу. Вращающие моменты, стремящиеся повернуть тело против часовой стрелки, считаются положительными, по часовой стрелке – отрицательными. В зависимости от их соотношения угловое ускорение также может быть положительным или отрицательным. Закон, выражаемый формулой (11), при изучении вращения тел играет ту же роль, что и второй закон Ньютона в динамике частиц. Внешний вид лабораторной установки представлен на рис. 1. Маятник Обербека состоит из двух стержней 1 длиной
Рис. 1 Вращая маятник Обербека, наматывают шнур 5 на барабан 4. При этом гиря 6 поднимается на некоторую высоту
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 5; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.111 (0.006 с.) |

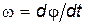 , (1)
, (1)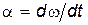 . (2)
. (2)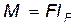 , (3)
, (3)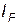 – плечо силы – кратчайшее расстояние от оси вращения до линии действия силы.
– плечо силы – кратчайшее расстояние от оси вращения до линии действия силы.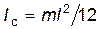 , (4)
, (4)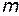 и
и 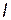 –соответственно масса и длина стержня.
–соответственно масса и длина стержня.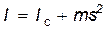 , (5)
, (5)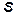 – расстояние между параллельными осями.
– расстояние между параллельными осями.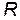 и размерами тела можно пренебречь (
и размерами тела можно пренебречь ( 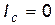 ), то его момент инерции
), то его момент инерции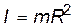 . (6)
. (6)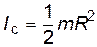 ; (7)
; (7)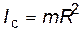 ; (8)
; (8)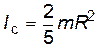 . (9)
. (9)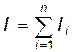 . (10)
. (10)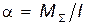 . (11)
. (11)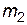 , закрепленных на валу 2 так, что ось вращения проходит через центр тяжести системы. На концах стержней укреплены четыре одинаковых груза 3 массой
, закрепленных на валу 2 так, что ось вращения проходит через центр тяжести системы. На концах стержней укреплены четыре одинаковых груза 3 массой 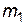 на расстоянии
на расстоянии 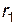 и
и 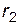 , на которые наматывается шнур 5. Шнур перекинут через ролик 7. К свободному концу шнура прикрепляется гиря 6 массой
, на которые наматывается шнур 5. Шнур перекинут через ролик 7. К свободному концу шнура прикрепляется гиря 6 массой 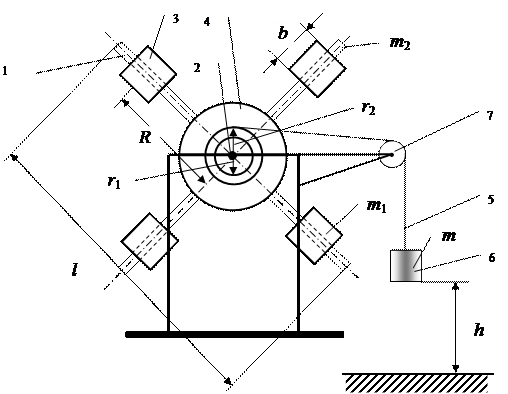
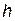 . Если освободить систему, то гиря под действием силы тяжести будет опускаться вниз. Сила натяжения нити передается барабану и создает вращающий момент, под действием которого маятник начинает вращаться. Время падения гири определяется по секундомеру, высота падения – линейкой, размеры деталей маятника – штангенциркулем.
. Если освободить систему, то гиря под действием силы тяжести будет опускаться вниз. Сила натяжения нити передается барабану и создает вращающий момент, под действием которого маятник начинает вращаться. Время падения гири определяется по секундомеру, высота падения – линейкой, размеры деталей маятника – штангенциркулем.


