
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если функция не относится ни к одному из указанных видов, то ее называют ни четной ни нечетной или функцией общего вида. У таких функций нет симметрии.Содержание книги
Поиск на нашем сайте
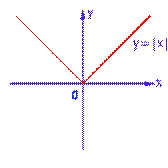
Функция называется четной, если при изменении знака аргумента, она не меняет свое значение. Формульная запись этого выглядит так . Это значит, что после подстановки в функцию на место всех иксов значений «минус икс», функция в результате не изменится. График такой функции симметричен относительно оси . Примерами четных функций являются К примеру, покажем симметричность графика
Если функция не относится ни к одному из указанных видов, то ее называют ни четной ни нечетной или функцией общего вида.У таких функций нет симметрии. Такой функцией, например, является недавно рассмотренная нами линейная функция Особым свойством функций является периодичность.Дело в том, что периодичными функциями, которые рассматриваются в стандартной школьной программе, являются только тригонометрические функции. Мы уже подробно о них говорили при изучении соответствующей темы. Периодичная функция – это функция, которая не меняет свои значения при добавлении к аргументу определенного постоянного ненулевого числа. Такое минимальное число называют периодом функции и обозначают буквой . Формульная запись этого выглядит следующим образом: Посмотрим на это свойство на примере графика синуса:
Вспомним, что периодом функций Как мы уже знаем, для тригонометрических функций со сложным аргументом может быть нестандартный период. Речь идет о функциях вида:
У них период равен
У них период равен Как видим, для вычисления нового периода стандартный период просто делится на множитель при аргументе. От остальных видоизменений функции он не зависит. Промежутки монотонности функции Очень важным свойством функции является ее монотонность. Зная это свойство различных специальных функций, можно определить поведение различных физических, экономических, социальных и многих других процессов. Выделяют следующие виды монотонности функций:
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 16; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.103.14 (0.009 с.) |

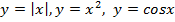 и др.
и др.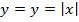 относительно оси
относительно оси 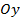 :
:
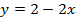 с графиком:
с графиком: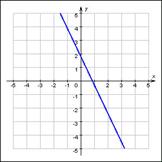
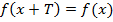 .
.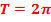

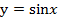 и
и 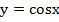 является
является 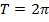 , а периодом
, а периодом 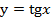 и
и 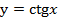 –
– 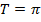 .
.
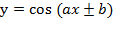
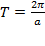 . И о функциях:
. И о функциях: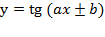
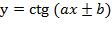
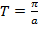 .
.


