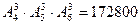Схема решения комбинаторных задач

Задача 6. Из 10 кандидатов нужно избрать: а) 3-х членов команды факультета для участия в университетском конкурсе «Что? Где? Когда?»;             в) капитана, аналитика и интерпретатора (для презентации) для участия команды факультета в педагогической олимпиаде. Сколькими способами это можно сделать?                        а) С103=720/6=120 ,       в)А103=10∙9∙8=720
Элементы комбинаторики

1.У мамы 3 яблока и 2 груши. Каждый день она дает сыну по одному фрукту. Сколькими способами это можно сделать в первый день?, за 5 дней?

2.В турнире участвуют 5 человек. Сколькими способами могут распределиться места между ними?

3.Сколько способов рассадки 12-ти гостей за круглым столом?, на каруселе?

4.Из цифр 1,2,3,4,5 составлены 5-тизначные числа, не кратные 5, не содержащие одинаковых цифр. Сколько существует таких чисел?

5. 30 книг: 27 книг различных авторов и 3-хтомник одного автора, помещены на одной полке. Сколькими способами можно расставить книги на полке так, чтобы книги одного автора стояли вместе?

6.Сколькими способами из 40 учеников класса можно выделить актив в следующем составе: староста, учебный сектор, редактор стенгазеты?

7.В шахматном турнире участвуют 5 школьников и 15 студентов. Сколькими способами могут распределяться места, занятые в турнире школьниками, если известно, что никакие 2 участника не набрали одинакового количества очков?

8.Четверо студентов сдают экзамен. Сколькими способами им могут быть поставлены отметки, если известно, что никто из них не получит неудовлетворительную оценку?

9.      Сколькими способами можно выбрать 3 ленты разных цветов из 5-ти лент разных цветов?

10.В шахматном турнире принимают участие 12 шахматистов. Сколько будет сыграно партий, если любые два участника встретятся между собой только один раз?

11.На шахматном турнире, проводившемся в один круг, была сыграна 91 партия. Сколько участников было на турнире?

12.Из отряда солдат в 40 человек, среди которых есть рядовой Иванов, назначаются в караул 3 человека. Сколькими способами может быть составлен караул? В скольких случаях в число караульных попадёт рядовой Иванов?

13.Из города А в город В ведет 5 дорог, а из В в С – три дороги. Сколько путей, проходящих через В, ведет из А в С?

14.Сколькими способами можно из 15 солдат и 4 офицеров назначить в  патруль трех солдат и одного офицера?

15.На железной дороге 25 станций. На каждом билете печатаются станция отправления и станция назначения. Сколько всего различных билетов нужно оформить, если: а) каждый билет действителен только в указанном направлении; б) каждый билет годен либо на поездку «туда», либо на поездку «обратно»?

16.В некоторой стране номера автомобилей состоят из двух букв, за которыми следуют две цифры, например АВ-53. Сколько различных номеров можно составить, если использовать 5 букв и 6 цифр (цифры и буквы в одном номере не повторяются)

17.От двух спортивных обществ, в каждом из которых по 40 фехтовальщиков, надо выделить по 3 фехтовальщика для участия в соревнованиях. Сколькими способами это можно сделать?

18.Собрание из 100 человек выбирает председателя, секретаря и трёх членов редакционной комиссии. Сколькими способами это можно сделать?

19.В кружке художественного слова занимаются 15 человек, в фортепьянном – 10, в вокальном – 13, в фотокружке – 20 человек. Сколькими способами можно составить бригаду из 4 чтецов, 3 пианистов,5 певцов и одного фотографа?

20.Для полета в космос необходимо укомплектовать следующий экипаж: командир корабля, первый помощник, второй помощник, два бортинженера и врач. Командная тройка может быть выбрана из 25 готовящихся к полету летчиков, два бортинженера – из 20 специалистов, врач – из 8 медиков. Сколькими способами можно укомплектовать экипаж?

21.Из четырёх математиков и пяти филологов требуется выбрать комиссию в составе четырёх человек при условии, что в комиссию войдёт хотя бы один математик и хоть один филолог. Сколькими способами это можно сделать?

22.Из 4 инженеров и 9 экономистов составляют комиссию, состоящую из 7 человек. Сколькими способами это можно сделать, если в комиссию должны войти хотя бы 2 инженера?

23.Сколько чётных пятизначных чисел можно образовать из цифр 0,1,2,3,4 при условии, что каждая цифра входит в число 1 раз?

24.Студенту необходимо сдать 4 экзамена за 9 дней. Сколькими способами это можно сделать, если известно, что последний экзамен он сдаёт на девятый день?

25.Известно, что в комнате студенческого общежития живут трое студентов. У них есть 4 чашки, 5 блюдец и 6 чайных ложек (все чашки, блюдца и ложки отличаются друг от друга). Сформулируйте вопрос к этому условию, чтобы получилась задача, имеющая своим решением следующую формулу:

26.У дизайнера имеется 5 различных стульев и 7 рулонов обивочной ткани различных цветов. Сколькими способами он может осуществить обивку стульев, если каждый стул декорируется только одним цветом ткани?

27.Из состава конференции, на которой присутствуют 52 человека, надо избрать президиум в составе 5 человек и делегацию в составе трех человек. Сколькими способами может быть произведен выбор, если члены президиума могут войти в состав делегации? А если не могут?

28. Из колоды, содержащей 52 карты, вынули 10 карт. Во скольких случаях среди этих карт есть хотя бы 1 туз? Ровно 1 туз?

29.Сколько нечетных и сколько четных четырехзначных чисел можно составить из цифр числа 3694, если каждую цифру надо использовать один раз.

30. На первые две линии произвольным образом ставятся белые и черные фигуры (король и ферзь каждого цвета, по 2 ладьи, 2 слона, 2 коня). Сколькими способами это можно сделать? А если расставлять на всей доске? А если расставлять и все пешки?

31. На званый вечер приглашены 5 мужчин и 5 женщин. Напротив каждого места на стол необходимо поставить табличку с именем того, кто будет на этом месте сидеть, но никакие два лица одного пола не должны сидеть рядом. Сколькими способами можно расставить таблички?