
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Некоторые частные режимы работы трехфазных цепейСодержание книги
Поиск на нашем сайте
1.3. Расчет трехфазных цепей Рассмотрим расчет трехфазной цепи звезда – звезда с нейтральным проводом (рис. 1.7). Расчет такой цепи можно производить всеми известными методами расчета разветвленных цепей. Чаще всего рационально применять метод узловых потенциалов, т.к. в этой схеме два узла O и O1, и для определения неизвестных токов и напряжений нужно составить одно уравнение. Примем потенциал точки О равным нулю, тогда напряжение нейтрали
Здесь
Напряжение на фазах нагрузки
Токи в фазах:
Рассмотрим несколько частных случаев. 1. Отсутствует сопротивление в нейтральном проводе 2. Сопротивления нагрузки одинаковы
Учитывая соотношение (1.11), векторные диаграммы напряжений на нагрузке и на генераторе совпадают и имеют вид, представленный на рис. 1.8, а.
Рассчитав треугольник, образованный, например, фазными напряжениями
Здесь 3. Нейтральный провод отсутствует, что соответствует схеме «звезда – звезда без нейтрального провода». Расчет производится по формулам (1.8, 1.9) с учетом того, что Замечание. В схеме «звезда – звезда без нейтрального провода» с симметричным генератором и несимметричной нагрузкой в случае равенства комплексных сопротивлений только в двух фазах напряжение нейтрали можно определить из соотношений
Покажем справедливость этих формул на примере
При соединении нагрузки в треугольник токи в его фазах определяются по закону Ома
Линейные токи находят по первому закону Кирхгофа
Из расчета треугольников, образованных двумя фазными токами (биссектрисы равностороннего треугольника) и линейным током, следует, что
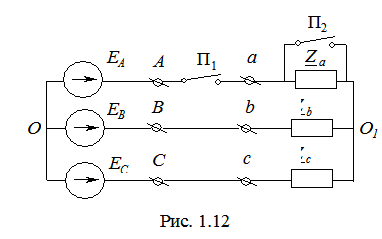
При несимметричной нагрузке векторные диаграммы токов имеют самый разнообразный вид. Пример такой диаграммы приведен на рис. 1.11, где Рассмотрим три режима работы схемы, представленной на рис. 1.12. 1.
по величине
Векторные диаграммы представлены на рис. 1.15. Ток в сопротивлениях
Таким образом, фазный ток и фазное напряжение неповрежденных фаз уменьшилось в
В этом режиме
Таким образом, фазные напряжения и токи неповрежденных фаз B и C увеличились в 1. Переключатели П1 и П2 замкнуты. При этом имеет место симметричный режим работы трехфазной цепи.
Все фазные токи
2. Переключатель П1 разомкнут (режим холостого хода или обрыв фазы bc).
3. Переключатель П1 замкнут, а переключатель П2 разомкнут (обрыв линии В). При этом трехфазная цепь преобразуется в однофазную, и все три сопротивления подключаются к напряжению
Таким образом, при обрыве линейного провода в фазах, гальванически связанных с ним, токи уменьшаются в два раза, в третьей фазе ток остается неизменным, линейный ток в неповрежденной линии уменьшается по сравнению с симметричным режимом в 1,15 раза.
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 6; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.67.248 (0.008 с.) |

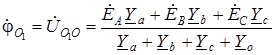 . (1.8)
. (1.8)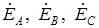 – комплексы ЭДС соответствующих фаз генератора,
– комплексы ЭДС соответствующих фаз генератора, 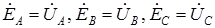 ;
;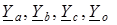 – комплексные проводимости соответствующих фаз нагрузки и нулевого провода.
– комплексные проводимости соответствующих фаз нагрузки и нулевого провода.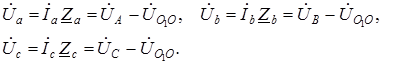 (1.9)
(1.9)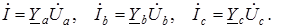 (1.10)
(1.10)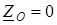 , тогда
, тогда 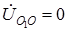 .
.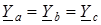 , нагрузка симметрична. Из (1.8) следует, что в этом случае также напряжение нейтрали
, нагрузка симметрична. Из (1.8) следует, что в этом случае также напряжение нейтрали 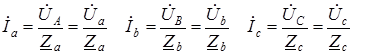 (1.11)
(1.11)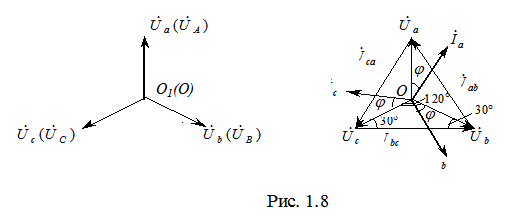
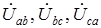 . Из диаграмм на рис. 1.8 очевидно, что модули всех линейных напряжений равны
. Из диаграмм на рис. 1.8 очевидно, что модули всех линейных напряжений равны 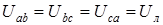 .
.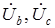 и линейным
и линейным 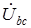 , получим
, получим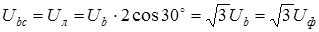 . (1.12)
. (1.12)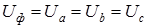 – модули фазного напряжения симметричной нагрузки.
– модули фазного напряжения симметричной нагрузки.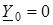 .
.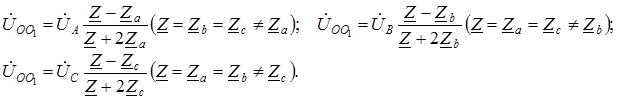
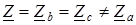 .
.
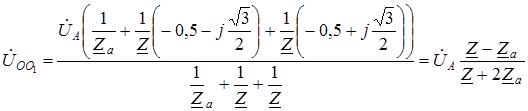
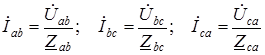 . (1.13)
. (1.13)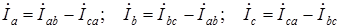 . (1.14)
. (1.14)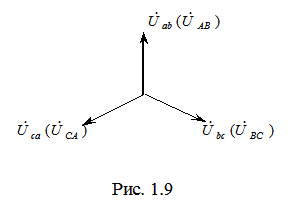 Поскольку линейные напряжения на нагрузке равны линейным напряжениям на генераторе, которые в свою очередь равны соответствующим ЭДС на обмотках генератора, векторная диаграмма линейных напряжений на нагрузке (рис. 1.9) полностью совпадает с векторной диаграммой генераторных ЭДС, приведенных на рис. 1.2.
Поскольку линейные напряжения на нагрузке равны линейным напряжениям на генераторе, которые в свою очередь равны соответствующим ЭДС на обмотках генератора, векторная диаграмма линейных напряжений на нагрузке (рис. 1.9) полностью совпадает с векторной диаграммой генераторных ЭДС, приведенных на рис. 1.2.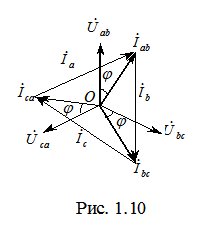 Пусть нагрузка симметрична и носит активно-индуктивный характер, тогда векторные диаграммы напряжений, фазных и линейных токов имеют вид, представленный на рис. 1.10. С помощью полученной диаграммы можно определить, что модули линейных токов равны (они являются сторонами равностороннего треугольника)
Пусть нагрузка симметрична и носит активно-индуктивный характер, тогда векторные диаграммы напряжений, фазных и линейных токов имеют вид, представленный на рис. 1.10. С помощью полученной диаграммы можно определить, что модули линейных токов равны (они являются сторонами равностороннего треугольника)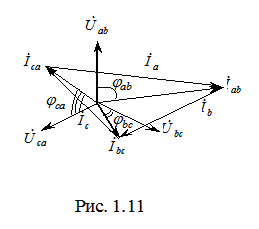
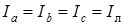 .
.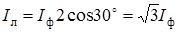 . (1.15)
. (1.15)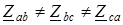 .
.
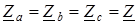 , переключатель П1 замкнут, переключатель П2 разомкнут. Имеет место симметричный режим работы трехфазной цепи
, переключатель П1 замкнут, переключатель П2 разомкнут. Имеет место симметричный режим работы трехфазной цепи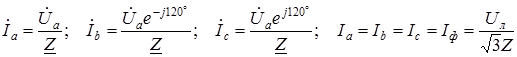 ,
,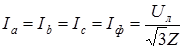 .
.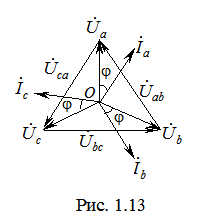 Векторные диаграммы при активно-индуктивной нагрузке представлены на рис. 1.13. Все фазные токи
Векторные диаграммы при активно-индуктивной нагрузке представлены на рис. 1.13. Все фазные токи 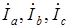 смещены относительно соответствующих фазных напряжений на угол j. Линейные напряжения опережают фазные напряжения на 30° (
смещены относительно соответствующих фазных напряжений на угол j. Линейные напряжения опережают фазные напряжения на 30° ( 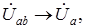
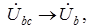
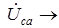
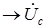 ).
).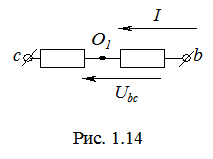 2. Переключатели П1 и П2 разомкнуты (режим холостого хода или обрыв фазы А). При этом схема из трехфазной цепи преобразуется в однофазную с напряжением
2. Переключатели П1 и П2 разомкнуты (режим холостого хода или обрыв фазы А). При этом схема из трехфазной цепи преобразуется в однофазную с напряжением 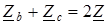 (рис. 1.14). Потенциал точки О1 становится равным
(рис. 1.14). Потенциал точки О1 становится равным 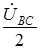 .
.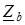 и
и 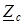 равен
равен 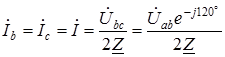 .
.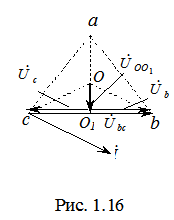
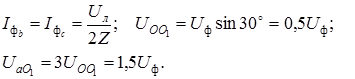
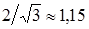 раза.
раза.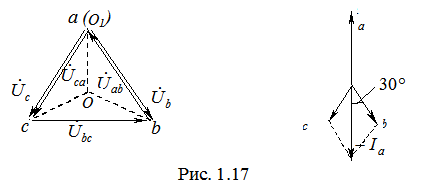
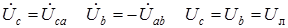 .
.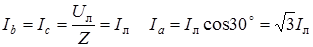 .
.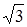 раз, а ток закороченной фазы (Ia) – в 3 раза по сравнению с симметричным режимом работы схемы.
раз, а ток закороченной фазы (Ia) – в 3 раза по сравнению с симметричным режимом работы схемы.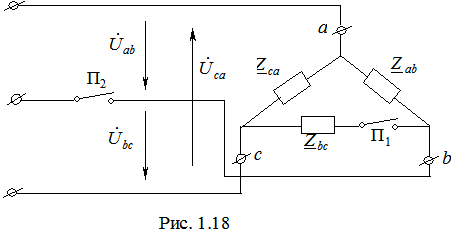
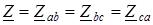 , соединенных треугольником, которые подключены к симметричной системе линейных напряжений
, соединенных треугольником, которые подключены к симметричной системе линейных напряжений 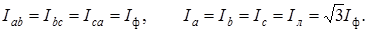 (1.16)
(1.16)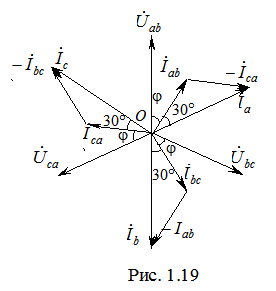 Векторные диаграммы напряжений и токов при активно-индуктивной нагрузке приведены на рис. 1.19.
Векторные диаграммы напряжений и токов при активно-индуктивной нагрузке приведены на рис. 1.19.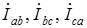 отстают от соответствующих фазных напряжений
отстают от соответствующих фазных напряжений 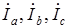 отстают от соответствующих фазных токов
отстают от соответствующих фазных токов 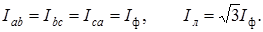 (1.17)
(1.17)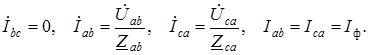 (1.18)
(1.18)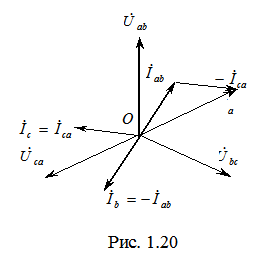 Линейные токи
Линейные токи 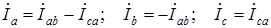 , т.е.
, т.е. 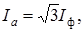
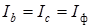 . Таким образом, линейный ток в проводе, не связанном гальванически с «поврежденной» фазой, остается неизменным по сравнению с симметричным режимом, а два других линейных тока
. Таким образом, линейный ток в проводе, не связанном гальванически с «поврежденной» фазой, остается неизменным по сравнению с симметричным режимом, а два других линейных тока 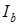 и
и 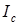 становятся равными фазным токам при симметричном режиме. Векторные диаграммы напряжений и токов приведены на рис. 1.20.
становятся равными фазным токам при симметричном режиме. Векторные диаграммы напряжений и токов приведены на рис. 1.20.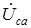 (рис. 1.21). Векторные диаграммы напряжений и токов для этой схемы представлены на рис. 1.22.
(рис. 1.21). Векторные диаграммы напряжений и токов для этой схемы представлены на рис. 1.22.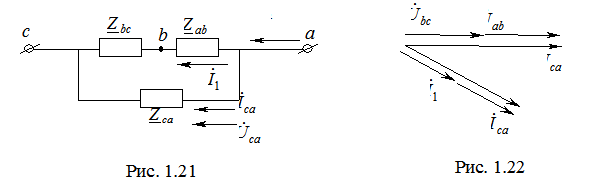
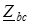 и
и 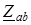
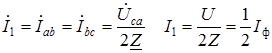 , ток в фазе ²ca²
, ток в фазе ²ca² 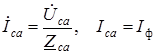 . Линейные токи
. Линейные токи 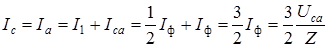 .
.


