
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные комбинаторные конфигурации.Содержание книги Поиск на нашем сайте
Основные комбинаторные конфигурации. 1. Выборки (сочетания); 2. Перестановки; 3. Подстановки; 4. Размещения; 5. Разбиения; 6. Перестановки с повторением; 7. Выборки с повторением.
Выборки (сочетания). Классической задачей КА является задача о числе выборок (сочетаний), содержание которой можно выразить следующим образом: сколькими способами можно выбрать m из n различных предметов? Пример 1. Сколькими способами можно выбрать 2 монеты из трех монет в 1, 2 и 3 копейки? Решение: {1,2}; {1,3}; {2,3}. Число всех возможных выборок из n предметов по m в каждой выборке обозначается Оно выражается формулой: Правило симметрии по выборкам:
Правило Паскаля: Доказательство:
что и требовалось доказать.
Пример 2. Есть шахматная доска 3 x 3 Сколькими способами можно выбрать пару клеток: белую и черную? I вариант: 4 способа для белой пары * 5 способов для чёрной пары = 20 способов. II вариант: Всего квадратов – 9. Тогда:
Тогда решение: Пример 3. Сколькими способами можно составить комиссию из трех человек, выбирая их из четырех супружеских пар, если в комиссию не могут входить члены одной семьи? Решение: Выбираем 3 семьи: Из каждой семьи берем по 1 человеку: Всего способов: 4*2*2*2=32.
|
||||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 8; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.122.20 (0.008 с.) |

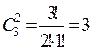
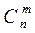
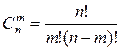
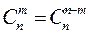
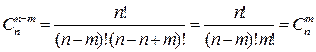
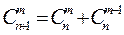
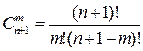

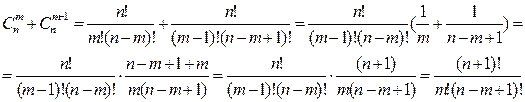

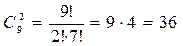 способов выбрать пару клеток.
способов выбрать пару клеток.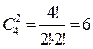 способов выбрать 2 белых.
способов выбрать 2 белых.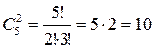 способов выбрать 2 черных.
способов выбрать 2 черных.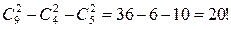
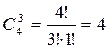 способа.
способа.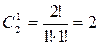 способа на семью.
способа на семью.


