
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка информативности экспериментаСодержание книги
Поиск на нашем сайте Дисперсия воспроизводимости Выполнение требования однородности построчных дисперсий
где Результаты расчета значений:
Проверка информативности эксперимента
где
Т. к.
Вычисление b – коэффициентов
где
где
где
Используя формулы (1.11), (1.12), (1.13) вычисляем b – коэффициенты уравнения (1.1):
Проверка значимости b – коэффициентов Вычисление b – коэффициентов проверяют по t-распределению на значимость. Вычисляют
где
где n – количество параллельных опытов в строке; N – количество комбинаций (опытов). Получим значение
Если Искомое уравнение регрессии имеет вид:
|
||
|
Последнее изменение этой страницы: 2024-06-17; просмотров: 32; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.006 с.) |

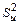 позволяет определить дисперсию воспроизводимости как среднеарифметическое построчных дисперсий:
позволяет определить дисперсию воспроизводимости как среднеарифметическое построчных дисперсий: (1.8)
(1.8) (1.9)
(1.9) - среднеквадратичное отклонение, ошибка опыта.
- среднеквадратичное отклонение, ошибка опыта. и
и  .
. (1.10)
(1.10) - число опытов в строках. Их значения численно равны количеству параллельных опытов. В нашем случае
- число опытов в строках. Их значения численно равны количеству параллельных опытов. В нашем случае  .
.
 находят по таблице t – распределения [2, прил. 3] по степени свободы
находят по таблице t – распределения [2, прил. 3] по степени свободы  и уровню значимости
и уровню значимости 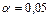 .
. , то результаты эксперимента признаются удовлетворительными.
, то результаты эксперимента признаются удовлетворительными. (1.11)
(1.11) - значение коэффициента при фиктивном
- значение коэффициента при фиктивном 
 – среднее значение выхода для
– среднее значение выхода для  -го опыта.
-го опыта. (1.12)
(1.12) - значение коэффициента при факторе
- значение коэффициента при факторе 

 (1.13)
(1.13) - значение коэффициента при парном воздействии факторов.
- значение коэффициента при парном воздействии факторов.







 .
. :
: (1.14)
(1.14) - параметр для t – распределения со степенями свободы
- параметр для t – распределения со степенями свободы  и уровнем значимости
и уровнем значимости 
 - среднее квадратичное отклонение
- среднее квадратичное отклонение  - коэффициентов.
- коэффициентов. (1.15)
(1.15)
 .
. , то соответствующий коэффициент незначим, и он исключается из уравнения регрессии (1.1). Таким образом, все коэффициенты, кроме
, то соответствующий коэффициент незначим, и он исключается из уравнения регрессии (1.1). Таким образом, все коэффициенты, кроме  ,
,  ,
,  , незначимы.
, незначимы. .
.


