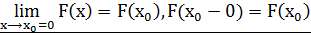Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Повторные независимые испытания.
14. Формула Бернулли. Наивероятнейшее число наступления события. Пусть в результате испытания возможно 2 исхода: 1)появится событие А; 2)появится противоположное событие тогда Где n-кол-во испытаний K-кол-во удачных испытании Ckn=n!/K!(n-K)! (без упорядочивания без возвращения!/) ПР: найти вероятность того, что стрелок попадёт 3 раза в мишень из 5 выстрелов, если вероятность попадания в мишень для стрелка 0,8 n=5 K=3 P=0,8 g=1-р=0,2 Наивероятнейшее число наступления события А в испытанмях Бернули np-g<m найвероятнейш.<np+p Пример: При автоматической наводке орудия вероятность попадания по быстро движущее цели=0,9. Найти найвероятнейшее число попаданий при 50 выстрелов. n 50 p=0,9 g=0,1 50*0,9*0,1<m<50*0,9*0,9* 44,9<m<45,9 m найв=45 Локальная формула Муавра-Лапласа. Если вероятность (р)появления события А в каждом испытании постоянно и отлично от 0 до 1, то вероятность Рn(К) того, что событие А в n испытаниях появятся ровно К раз, приближенно равно: Рn(К)=
Прим: Найти вероятность того, что событие А наступят ровно 80 раз из 400 испытаний. Вероятность появления события А=0,2 n=400 K=80 p=02 g=08 Интергральная формула Муавра-Лапласа. Если вероятность наступления события А в каждом испытании постоянно и отлично от 0 и 1, то Рn(XK1, XK2) или Рn(К1, К2), то событие А появится в n испытаниях от К1 до К2 раз приближенно равно Рn(К1, К2)=Ф(XK2)-Ф(XK1).
Формула Пуассона Если вероятность наступления события А в каждом испытании постоянно но мала, а число независимых испытаний достаточно велико ПРИМЕР: Пусть вероятность изготовления нестандартных деталей =0,004. Найти вероятность того что среди 1000 деталей окажется h 5 нестандартных. P=0,004 m=5 n=10000
е=2,7
18.Случайная величина. Случайной величиной можно назвать числовую функцию х( Сущ. 2 типа случ. величин: 1)дискретная- случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности;
2) непрерывная- случайная величина, которая может принимать все значения из некоторого промежутка ПР: Дважды подбрасываем монету Ὼ={(гг)(рр)(рг)(гр)} Рассмотрим СВх Х=(Число выпадения герба) Получим табл.
Случайные величины наз дискретной -если они принимает конечное либо счетное число значений. Функцией распределения случайных величин называется функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате реализации эксперимента значение, меньшее, чем заданное х. Функция распределения F(x) случайной величины Х имеет следующие свойства: 1. Все значения функции распределения F(x) принадлежат отрезку [0, 1], т.е. 0≤ F(x) ≥1. 2. Функция распределения F(x) является неубывающей, т.е. если З. Функция F(x) в точке
4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то для ее функции распределения F(x) F(x) = о при х≤ а, F(x) = 1 при х≥b.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 35; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.36.213 (0.008 с.) |
 . Проводим n испытаний, события независимы и Р(А)=р, Р(
. Проводим n испытаний, события независимы и Р(А)=р, Р( =q=1-р
=q=1-р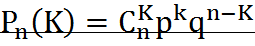 .
. .
.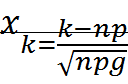
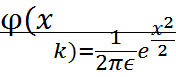
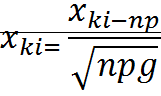
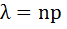 также неброльшое (не больше 10)то вероятность того, что в этих испытаниях событие А наступит К-раз ͌
также неброльшое (не больше 10)то вероятность того, что в этих испытаниях событие А наступит К-раз ͌ 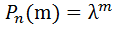 /
/ 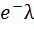
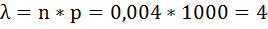
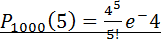 =0?1563
=0?1563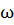 ) элементарного события
) элементарного события 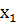 <
< 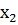 , то F(
, то F(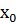 непрерывна слева, Т.е.
непрерывна слева, Т.е.