Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предмет теории вероятностей. Возникновение теории вероятностей.Стр 1 из 6Следующая ⇒
Предмет теории вероятностей. Возникновение теории вероятностей. Возникла ТВ относительно в17 веке. Интерес к задачам формируется под валянием развития страхового дела. На те частные вопросы на, которые побудили математиков поразмыслить над этим предметом были поставлены связи с азартными играми. Традиционные задачи стали: 1. Бросание игральной кости. 2. Извлечение карт из колоды. 3. Извлечение карт из колоды. Эти задачи являются тренировочными, а в некоторых случаях выступают в роли наглядных моделей для более серьёзных вероятностных схем. В основе вероятностных схем лежит понятие случайность и неопределенность. Зарождение Т,В, связано с исследованиями ПОСКАЛЯ И ФЕРМА кем и было сформатировано понятие В. Кроме указанного влияния запросов страхового дела задачи на вычисление вероятности ставили статистика народов населения и теория методов обработки наблюдения все это было связано с возникновением новых экономических отношении и с новыми научными проблемами.
ТВ - это математическая наука изучающая закономерности случайных явлений, особого рода законы управляющие случайными величинами. Она изучает св-ва случайных массовых событий способных многократно повторяться при воспроизведении определенного комплекса условий.
Действия над событиями (объединение, пересечение, разность). Объединением двух событий А и В называется событие С, состоящее в выполнении события А или события В, или обоих событий вместе. Пересечением событий А и В называется событие, состоящее из элементарных событий принадлежащих и событию А и событию В. Разность двух событий А и В называется событие, состоящее из элементарных событий, которые входят в событие А, но не входят в событие В. Операции над событиями: 1)Объединение(Сумма)-это А Ṳ В=А+В ПР:А=(123…9) В=(56…12) АṲВ=(123….12)
Пересечение(произведение)- А∩В=А*В ПР: А=(123…9) В=(56…12) А∩В=(56…9)
3)Разность - ПР: А=(123…9) В =(56…12) А/ В=(12…34)
Классическое определение вероятности. Равнозначными событиями наз - если условия испытания обеспечивают одинаковую возможность осуществления, каждого из них. Вероятность события называется отношение числа исходов благоприятствующих данному событию, к числу всех возможных исходов.
n - число всех равновозможных элементарных исходов опыта, образующих полную группу событий.
Ὼ{(гг)(рр)(рг)(гр)} А=(Выпадает худобы один раз герб) Р(А)=? Р(А)= m / n =3/4 m =3 n =4
Теоремы сложения вероятности. Теорема: Вероятность появления хотя бы одного из совместных событий равна сумме вероятностей этих событий без вероятности их совместного появления (если события А и В совместны): Р(А+В)=Р(А)+Р(В)-Р(АВ). Пусть А1, А2…Аn несовместные, то вероятность их суммы: Р(А1+А2+…+Аn)=Р(А1)+Р(А2)+…+Р(Аn). Два события называются совместными в данном опыте, если появление одного из них не исключает, появление другого в этом опыте. Так, при подбрасывании двух симметричных монет, события А - "герб на верхней стороне первой монеты" и В - "цифра на верхней стороне второй монеты" являются совместными.
Два события называются несовместными, если они не могут произойти вместе при одном и том же испытании. Например, несовместными являются попадание и промах при одном выстреле. Несколько событий называются несовместными, если они попарнонесовместны. Формула полной вероятности. Если событие А может произойти при появление одной из гипотез, то его вероятность равна сумме произведений вероятностей каждой гипотезы и соответствующих условных вероятностей события А: Формула Байеса. Пусть событие А происходит одновременно с одним из n-несовместных событий Н1, Н2…Нn и вероятности Р(Нi)
Формула Пуассона Если вероятность наступления события А в каждом испытании постоянно но мала, а число независимых испытаний достаточно велико
ПРИМЕР: Пусть вероятность изготовления нестандартных деталей =0,004. Найти вероятность того что среди 1000 деталей окажется h 5 нестандартных. P=0,004 m=5 n=10000
е=2,7
18.Случайная величина. Случайной величиной можно назвать числовую функцию х( Сущ. 2 типа случ. величин: 1)дискретная- случайная величина, принимающая различные значения, которые можно записать в виде конечной или бесконечной последовательности; 2) непрерывная- случайная величина, которая может принимать все значения из некоторого промежутка ПР: Дважды подбрасываем монету Ὼ={(гг)(рр)(рг)(гр)} Рассмотрим СВх Х=(Число выпадения герба) Получим табл.
Случайные величины наз дискретной -если они принимает конечное либо счетное число значений. Функцией распределения случайных величин называется функция F(x) действительной переменной х, определяющая вероятность того, что случайная величина Х примет в результате реализации эксперимента значение, меньшее, чем заданное х. Функция распределения F(x) случайной величины Х имеет следующие свойства: 1. Все значения функции распределения F(x) принадлежат отрезку [0, 1], т.е. 0≤ F(x) ≥1. 2. Функция распределения F(x) является неубывающей, т.е. если З. Функция F(x) в точке
4. Если все возможные значения случайной величины Х принадлежат интервалу (а, b), то для ее функции распределения F(x) F(x) = о при х≤ а, F(x) = 1 при х≥b.
Распределение Пуассона СВ. Если вероятность р события в каждом испытании при неограниченном увеличении числа испытаний n, изменяется т.о., что np= то вероятность того, что некоторое событие появится m раз в n испытаниях стремится к величине Рn(m) Закон распределения Пуассона: М(х)= D(х)= Έ= 26.Нормальный закон распределение СВ (распределение Гаусса). Случайная величина Х распределена по нормальному закону, если плотность распределения имеет вид: Р(х)= а=М(х)
Вер.попад.норм.распре-ной случ.вели-ны в интервал (α;β) вычисляется по формуле: P(α<x<β)=Ф( Для ее вычисления используются специальные таблицы или методы приближенного вычисления. 27. Геометрическое распределение случайной величины Неравенство Чебышева. Оценим вероятность отклонения СВ от ее мат ожидания по абсолютному значению, т.е. P{|X-M(X)|≥
Закон больших величин. Если 1) При достаточно большом числе п СВ имеющих 2) ограниченные дисперсии почти достоверно, что отклонение среднеарифметической СВ от среднеарифметического их мат ожидания будет сколь угодно мало по абсолютной величине.
Без доказательства (на основании неравенства Чебышева). На практике СВ Хi имеет одно и тоже мат ожидание, равное а, тогда последнее неравенство можно представить в виде: Теорема Бернулли. Если в каждой из п независимых испытаниях вероятность р появления события А постоянно, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число п достаточно велико: КРИТЕРИЙ СОГЛАСИЯ ПИРСОНА. Если закон распределения неизвестен, но есть основания предполагать, что он имеет определенный вид (назовем его А), то проверяют нулевую гипотезу: генеральная совокупность распределена по закону А. Проверка этой гипотезы производится при помощи специально подобранной случайной величины – критерия согласия. Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия, наиболее часто используемым является критерий согласия К.Пирсона («хи квадрат»). Ограничимся применением критерия Пирсона к проверке гипотезы о нормальном распределении генеральной совокупности.
ОСНОВНЫЕ ПОНЯТИЯ КОРРЕЛЯЦИОННОГО И РЕГРЕССИОННОГО АНАЛИЗА. Под регрессией понимается функциональная зависимость между объясняющими переменными и условным математическим ожиданием (средним значением) зависимой переменной Y, которая строится с целью предсказания (прогнозирования) среднего значения Y при фиксированных значениях независимых переменных. Корреляционно-регрессионный анализ включает в ceбя измерение тесноты и направления связи, а также установление аналитического выражения (формы) связи. Задачи корреляционного анализа сводятся к измерению тесноты связи между варьирующими признаками, определению неизвестных причинных связей и оценке факторов, оказывающих наибольшее влияние на результативный признак. Задачи регрессионного анализа лежат в сфере установления формы зависимости, определения функции регрессии, использования уравнения для оценки неизвестных значении зависимой переменной.
43)Линейная корреляционная зависимость и прямые регрессии Другими словами, корреляционная зависимость – это согласованное изменение двух признаков, отражающее тот факт,что изменчивость одного признака находится в соответствии с изменчивостью другого. В дальнейшем рассмотрении мы ограничимся лишь линейными корреляционными за- висимостями как наиболее простыми. Как известно (см. п. 12), величина, характеризующая степень линейной зависимости с. в. X иY, – это коэффициент корреляцииR xy выборочный коэффициент корреляции:
Линейная зависимостьY от X задается формулойпрямой линейной регрессии Y на X
а линейная зависимость X отY задается формулой прямой линейной регрессии X на Y
44)Коэффициент линейной корреляции и его свойства Коэффициент линейной корреляции отражает меру линейной зависимости между двумя переменными. Предполагается, что переменные измерены в интервальной шкале либо в шкале отношений. Общая формула
Коэффициент корреляции обладает свойствами: 1.если S и n,независимы то, 2.всегда 3.
Предмет теории вероятностей. Возникновение теории вероятностей. Возникла ТВ относительно в17 веке. Интерес к задачам формируется под валянием развития страхового дела. На те частные вопросы на, которые побудили математиков поразмыслить над этим предметом были поставлены связи с азартными играми. Традиционные задачи стали: 1. Бросание игральной кости. 2. Извлечение карт из колоды. 3. Извлечение карт из колоды. Эти задачи являются тренировочными, а в некоторых случаях выступают в роли наглядных моделей для более серьёзных вероятностных схем. В основе вероятностных схем лежит понятие случайность и неопределенность. Зарождение Т,В, связано с исследованиями ПОСКАЛЯ И ФЕРМА кем и было сформатировано понятие В. Кроме указанного влияния запросов страхового дела задачи на вычисление вероятности ставили статистика народов населения и теория методов обработки наблюдения все это было связано с возникновением новых экономических отношении и с новыми научными проблемами.
ТВ - это математическая наука изучающая закономерности случайных явлений, особого рода законы управляющие случайными величинами. Она изучает св-ва случайных массовых событий способных многократно повторяться при воспроизведении определенного комплекса условий.
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2022-01-22; просмотров: 41; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.84.29 (0.057 с.) |
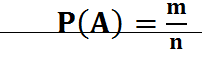 . где m - число элементарных исходов, благоприятствующих событию А;
. где m - число элементарных исходов, благоприятствующих событию А;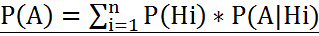
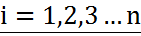 известны до опыта. Производится опыт в результате которого зарегистрировано появление события А при чём известно, что это событие имело определённые условные вероятности Р(А/Нi) i=1,2…n и требуется найти вероятности события Нi, если известно что событие А произошло.
известны до опыта. Производится опыт в результате которого зарегистрировано появление события А при чём известно, что это событие имело определённые условные вероятности Р(А/Нi) i=1,2…n и требуется найти вероятности события Нi, если известно что событие А произошло. 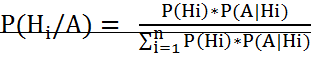 .
.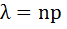 также неброльшое (не больше 10)то вероятность того, что в этих испытаниях событие А наступит К-раз ͌
также неброльшое (не больше 10)то вероятность того, что в этих испытаниях событие А наступит К-раз ͌ 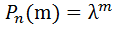 /
/ 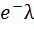
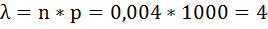
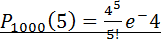 =0?1563
=0?1563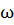 ) элементарного события
) элементарного события 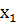 <
< 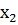 , то F(
, то F(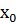 непрерывна слева, Т.е.
непрерывна слева, Т.е.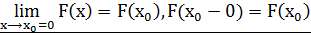
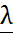 ,
, 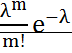 , т.е.
, т.е.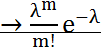 при n
при n 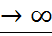 .
.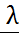
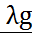
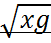
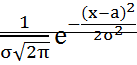 .
.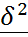 =Д(х)
=Д(х)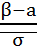 ) – Ф(
) – Ф(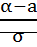 ). Функция Лапласа не выражается через элементарные функции
). Функция Лапласа не выражается через элементарные функции 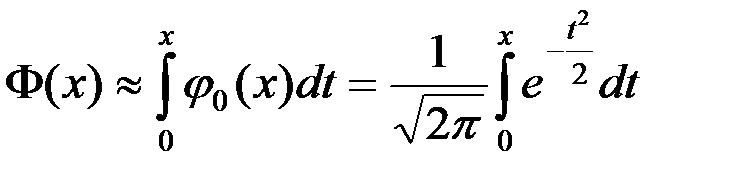 .
.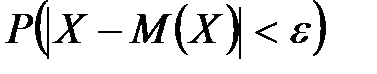 . Впервые это неравенство было доказано Чебышевым. Вероятность того, что отклонение СВ Х от ее мат ожидания меньше положительного числа ε не меньше, чем
. Впервые это неравенство было доказано Чебышевым. Вероятность того, что отклонение СВ Х от ее мат ожидания меньше положительного числа ε не меньше, чем 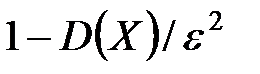 .
.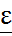 }≤
}≤ 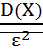 .
.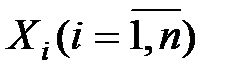 попарно независимы СВ, причем их дисперсия равномерно ограничены
попарно независимы СВ, причем их дисперсия равномерно ограничены 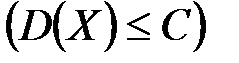 , где C=const, то как бы ни было мало положительное число ε вероятность неравенства
, где C=const, то как бы ни было мало положительное число ε вероятность неравенства 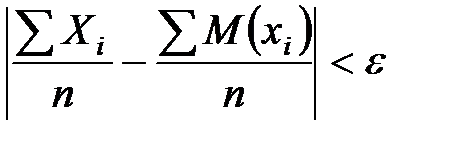 будет сколь угодно близка к единице, если число СВ достаточно велико:
будет сколь угодно близка к единице, если число СВ достаточно велико: 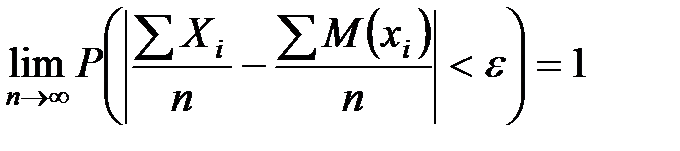 . Т.О. это означает:
. Т.О. это означает: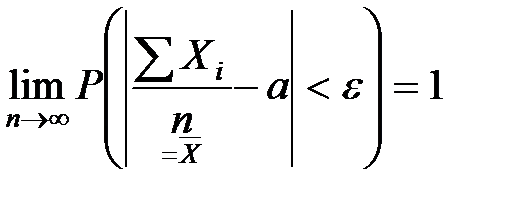 .
.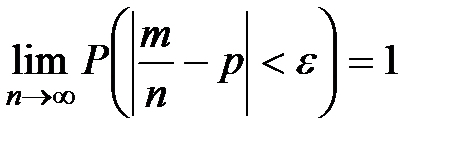
 где
где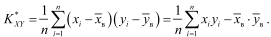
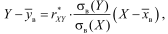
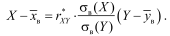
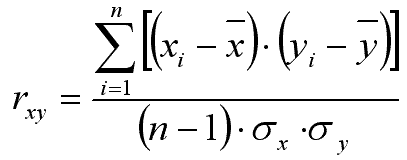 Где xi и yi - сравниваемые количественные признаки, n – число сравниваемых наблюдений, σx и σy – стандартные отклонения в сопоставляемых рядах.
Где xi и yi - сравниваемые количественные признаки, n – число сравниваемых наблюдений, σx и σy – стандартные отклонения в сопоставляемых рядах.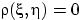
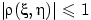
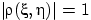 тогда и только тогда, когда S и n п. н. линейно связаны, т.е. существуют числа a неравно 0 и b такие, что
тогда и только тогда, когда S и n п. н. линейно связаны, т.е. существуют числа a неравно 0 и b такие, что