
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заполнить остальные столбцы.Содержание книги
Поиск на нашем сайте
В соответствии с таблицами истинности соответствующих логических операций, причем при заполнении каждого столбца операции выполняются над значениями одного или двух столбцов, расположенных левее заполняемого. Итак, вычисляем значения 3-го столбца по значениям 2-го, потом значения 4-го – по значениям 1-го и 2-го…
Вывод: получили в последнем столбце все единицы. Значит, значение сложного высказывания истинно при любых значениях простых высказываний К и С. Следовательно, учитель рассуждал логически правильно.
Основные законы логики: А = А – закон тождества (Всякое высказывание тождественно самому себе) А & A Ú
Кроме логических законов, важное значение для выполнения преобразований логических выражений имеют правила алгебраических преобразований. Многие из них имеют аналоги в обычной алгебре. Свойства констант: А Ú 0 = А А & 0 = 0 А Ú 1 = 1 А & 1 = 1 -------------------------------------------------------------------------------------------------------------------------------------------- Законы идемпотентности: А Ú А = А А & А = A -------------------------------------------------------------------------------------------------------------------------------------------- Законы коммутативности: (В обычной алгебре слагаемые и множители можно менять местами. В алгебре высказываний можно менять местами логические переменные при операциях логического умножения и логического сложения) А Ú В = В Ú А (Логическое сложение) А & В = В & А (Логическое умножение) -------------------------------------------------------------------------------------------------------------------------------------------- Законы ассоциативности (Если в логическом выражении используются только операция логического умножения или только операция логического сложения, то можно пренебрегать скобками или произвольно их расставлять): А Ú (В Ú С) = (АÚ В) Ú С А & (В & С) = (А & В) & С -------------------------------------------------------------------------------------------------------------------------------------------- Законы дистрибутивности:(В отличие от обычной алгебры, где за скобки можно выносить только общие множители, в алгебре высказываний можно выносить за скобки как общие множители, так и общие слагаемые): А Ú (В & С) = (АÚ В) & (А Ú С) Дистрибутивность сложения относительно сложения А & (В Ú С) = (А & В) Ú (А& С) Дистрибутивность умножения относительно умножения -------------------------------------------------------------------------------------------------------------------------------------------- Законы поглощения: А Ú (А & В) = А А & (А Ú В) = А -------------------------------------------------------------------------------------------------------------------------------------------- Законы де Моргана:
-------------------------------------------------------------------------------------------------------------------------------------------- Рассмотрим в качестве примера применения законов логики и правил алгебры логики преобразование логического выражения. Пусть нам необходимо упростить логическое выражение: (А &. В) v (A & В). Воспользуемся правилом дистрибутивности и вынесем за скобки А: (А & В) v (А & В) = А & (В v В). По закону исключенного третьего В v В = 1, следовательно: А & (В v B) = А & 1 = А. Базовые логические элементы компьютера
Логический элемент И конъюнктор
Логический элемент ИЛИ дизъюнктор
Логический элемент НЕ инвертор
Развитие человечества не было бы возможно без обмена информацией. С давних времен люди из поколения в поколение передавали свои знания, извещали об опасности или передавали важную и срочную информацию, обменивались сведениями. Например, в Петербурге в начале XIX века была весьма развита пожарная служба. В нескольких частях города были построены высокие каланчи, с которых обозревались окрестности. Если случался пожар, то на башне днем поднимался разноцветный флаг (с той или иной геометрической фигурой), а ночью зажигалось несколько фонарей, число и расположение которых означало часть города, где произошел пожар, а также степень его сложности.
В любом процессе передачи или обмене информацией существует ее источник и получатель, а сама информация передается по каналу связи с помощью сигналов: механических, тепловых, электрических и др. В обычной жизни для человека любой звук, свет являются сигналами, несущими смысловую нагрузку. Например, сирена — это звуковой сигнал тревоги; звонок телефона — сигнал, чтобы взять трубку; красный свет светофора — сигнал, запрещающий переход дороги.
При передаче информации важную роль играет форма представления информации. Она может быть понятна источнику информации, но недоступна для понимания получателя. Люди специально договариваются о языке, с помощью которого будет представлена информация для более надежного ее сохранения. Прием-передача информации могут происходить с разной скоростью. Количество информации, передаваемое за единицу времени, есть скорость передачи информации или скорость информационного потока. Очевидно, эта скорость выражается в таких единицах, как бит в секунду (бит/с), байт в секунду (байт/с), килобайт в секунду (Кбайт/с) и т.д. К сожалению, в отношении трактовки приставок существует неоднозначность. Встречается два подхода:
Применяются оба подхода, хотя для бита правильным считается «стандартный» подход, в отличии от байта, с которым «компьютерный» подход признают основным за традиционность. К битам, «компьютерный» подход применяют, преимущественно в компьютерной технике и программах. Максимальная скорость передачи информации по каналу связи называется п ропускной способностью канала. Следует упомянуть еще одну единицу измерения скорости передачи информации – бод. Бод (англ. baud) в связи и электронике — единица скорости передачи сигнала, количество изменений информационного параметра несущего периодического сигнала в секунду. Названа по имени Эмиля Бодо, изобретателя кода Бодо — кодировки символов для телетайпов. Зачастую, ошибочно считают что бод это количество бит переданное в секунду. В действительности же, это верно лишь для двоичного кодирования, которое используется не всегда. Например, в современных модемах используется квадратурная амплитудная манипуляция (КАМ), и одним изменением уровня сигнала может кодироваться несколько (до 16) бит информации. Например, при скорости изменения сигнала 2400 бод, скорость передачи может составлять 9600 бит/c, благодаря тому, что в каждом временном интервале передаётся 4 бита. Кроме этого, бодами выражают полную емкость канала, включая служебные символы (биты), если они есть. Эффективная же скорость канала выражается другими единицами, например битами в секунду. Одним из самых совершенных средств связи являются оптические световоды. Информация по таким каналам передается в виде световых импульсов, посылаемых лазерным излучателем. Оптические каналы отличаются от других высокой помехоустойчивостью и пропускной способностью, которая может составлять десятки и сотни мегабайт в секунду. Например, при скорости 50 Мбайт/с в течении 1 секунды передается объем информации, приблизительно равный содержанию 10 школьных учебников. 8. Системы счисления. Позиционные и непозиционные системы счисления. Алгоритмы перевода чисел из одной системы счисления в другую (стандартным способом, с помощью таблиц перевода). КОДИРОВАНИЕ информации - представление информации в той или иной стандартной форме. Например, письменность и арифметика - кодирование речи и числовой информации, музыку кодируют с помощью нот. Чтобы использовать числа их нужно как-то записывать и называть. СИСТЕМЫ СЧИСЛЕНИЯ - способы кодирования числовой информации,т.е. способ записи чисел с помощью некоторого алфавита, символы которого называют цифрами. В зависимости от способов изображения чисел цифрами, системы счисления делятся на непозиционные и позиционные. Непозиционной системой называется такая, в которой количественное значение каждой цифры не зависит от занимаемой ей позиции в изображении числа (римская система счисления). Позиционной системой счисления называется такая, в которой количественное значение каждой цифры зависит от её позиции в числе (арабская система счисления). Количество знаков или символов, используемых для изображения числа, называется основанием системы счисления. В древнем Вавилоне делили час на 60 мин., угол на 360 градусов, англосаксы начали делить год на 12 месяцев, сутки на два периода по 12 часов, продолжительность года 360 суток. В Риме семь чисел обозначают буквами. 1-I, 5-V, 10-X, 50- L,100-C, 500-D, 1000-M IV (4=5-1) Значение числа определяется как сумма или разность цифр числа. Это НЕПОЗИЦИОННАЯ СИСТЕМА СЧИСЛЕНИЯ. Славяне числа кодировали буквами а=1, В=2, Г=3; чтобы избежать путаницы ставился специальный знак ~ титло АЛФАВИТНАЯ система счисления. Славянская нумерация сохранялась до конца XVII века. При ПетреI возобладала т.называемая арабская нумерация. Славянская нумерация сохранилась в богослужебных книгах. Самой популярной системой кодирования чисел оказалась позиционная, десятичная. Используются десять цифр. Значение каждой определяется той позицией, которую цифра занимает в записи числа. Напр., 23 -три единицы, два десятка 32 -две единицы, три десятка 400 -4 сотни, два 0 вклад в число не дают, нужны для того,чтобы указывать позицию 4. В десятичной позиционной системе особую роль играет число 10 и его степени, например, 1996 - 6 единиц, 9 десятков, 9 сотен 1 тысяча или 1996=6+9*10+9*100+1*1000, т.к.1000=103 в третьей степени, 100=102, 10=101, т.о. 1996=1*103 + 9*102 + 9*101 +6*100. ЛЮБОЕ ЧИСЛО В НУЛЕВОЙ СТЕПЕНИ РАВНО ЕДИНИЦЕ 0,10 = 1 Т.е. любое 4-х значное число можно записать в следующем виде: N=a3*103+a2*102+a1*101+a0*100 a3, a2, a1, a0-десятичные цифры, от 1 до 9 или коэффициенты 3 2 1 0 -разряды, степени Но основанием системы может быть не обязательно число 10, т.о. мы можем записать число в N=an*Pn+an-1*Pn-1+...+a1*P1+a0*P0 Если взять за основание 60, то придется использовать 60 разных цифр. Такая система была в Древнем Вавилоне. Если основанием возьмем 2, получим систему всего с двумя цифрами: 199510=111110010112 Система счисления, где 2 является основанием системы называется ДВОИЧНОЙ СИСТЕМОЙ СЧИСЛЕНИЯ относится к МАШИННОЙ СИСТЕМЕ СЧИСЛЕНИЯ, к машинным системам счисления относятся и восьмиричная и шестнадцатиричная. Т.о. существуют следующие системы счисления: ВАВИЛОНСКАЯ,РИМСКАЯ,АЛФАВИТНЫЕ, АНАТОМИЧЕСКИЕ, МАШИННЫЕ Системы счисления делятся так же на ПОЗИЦИОННЫЕ И НЕПОЗИЦИОННЫЕ. ПЕРЕВОД ИЗ ДВОИЧНОЙ В ДЕСЯТИЧНУЮ СИСТЕМУ СЧИСЛЕНИЯ Как узнать чему равно девятизначное двоичное число N=1111101002 Подпишем сверху каждый разряд 87654321010 - 1 разряды (степени двойки) 1111101002 Т.о.111110100=1*28 +1*27 +1*26 +1*25 +1*24 +0*23 +1*22 +0*21 +0*20 =1*256+1*128+1*64 +1*32 +1*16 +0*8 +1*4 +0*2 +0*1=256 + 128 + 64 + 32 + 16 + 0 + 4 + 0 +0 =500 ПЕРЕВОД В ДВОИЧНУЮ СИСТЕМУ СЧИСЛЕНИЯ ЧИСЕЛ ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ
Выписав все остатки, начиная с последнего 3 в обратном порядке,получим двоичное разложение числа. 23410 = 111010102 ВОСЬМЕРИЧНАЯ И ШЕСТНАДЦАТЕРИЧНАЯ СИСТЕМЫ СЧИСЛЕНИЯ Запись числа в двоичной системе удобна для компьютера, но громоздка для человека. На помощь приходят системы, родственные двоичной ВОСЬМИРИЧНАЯ СИСТЕМА СЧИСЛЕНИЯ использует 8 цифр: 0,1,2,3,4,5,6,7. Единица, записанная в самом младшем разряде означает просто единицу (1*8 в нулевой степени), та же единица в следующем разряде обозначает 8 (1*8 в первой), в следующем 64(1*8 во второй)и т.д. 2 1 0 1- разряды (степени восьмерки) 8 - это 2 в третьей степени. При переводе в восьмиричную систему двоичное число из трех записывается одной цифрой.
Для перевода из двоичной в восьмиричную число, записанное в двоичной системе делим на триады справа налево Для перевода числа из восьмиричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную систему, представив каждую цифру в виде триады (1 в двоичной системе 1 добавляем до триады впереди 00) Еще компактней выглядит запись двоичного числа в ШЕСТНАДЦАТИРИЧНОЙ СИСТЕМЕ СЧИСЛЕНИЯ. Для первых 10 из 16 шестнадцатиричных цифр используются привычные цифры 0 1 2 3 4 5 6 7 8 9, а для остальных используют первые буквы латинского алфавита Цифра 1 в самом младшем разряде означает 1, в следующем разряде означает 16 (в первой степени), в следующем разряде 16*16 (162)=256, в следующем разряде 1*163 и т.д. 10016 =25610 Цифра F, записанная в самом младшем разряде означает 15 в десятичной системе, F в следующем разряде означает 15*16 в первой степени в десятичной системе и т.д. 2 1 0 - 1 разряды (степени числа 16) 2 1 0 16 - это 2 в четвертой степени. При переводе из двоичной системы в шестнадцатиричную число двоичное число из 4-х цифр кодируется числом из одной цифры в шестнадцатиричной системе. Для перевода числа из шестнадцатеричной системы в двоичную достаточно заменить каждую цифру на ее перевод в двоичную, представив каждую цифру в виде сочетания четырех 1 и 0
Как осуществить перевод чисел из двоичной системы в шестнадцатиричную? Необходимо разбить число, записанное в двоичной системе на группы по 4 разряда справа налево, заменив каждую группу одной шестнадцатиричной цифрой
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 358; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.183.186 (0.014 с.) |

 = 0 – закон непротиворечия (Высказывание не может быть одновременно истинным и ложным. Если высказывание А — истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно: A & A = 0)
= 0 – закон непротиворечия (Высказывание не может быть одновременно истинным и ложным. Если высказывание А — истинно, то его отрицание не А должно быть ложным. Следовательно, логическое произведение высказывания и его отрицания должно быть ложно: A & A = 0) = А – закон двойного отрицания (Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание: A = A)
= А – закон двойного отрицания (Если дважды отрицать некоторое высказывание, то в результате мы получим исходное высказывание: A = A) = 1
= 1  = 0
= 0
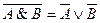








 Пусть нужно перевести в двоичную систему число 234. Будем делить 234 последовательно на 2 и запоминать остатки, не забывая про нулевые.
Пусть нужно перевести в двоичную систему число 234. Будем делить 234 последовательно на 2 и запоминать остатки, не забывая про нулевые.


