
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Моделювання взаємодії тягача і причепа при гальмуванніСодержание книги
Поиск на нашем сайте
Мета: дослідження динаміки процесу взаємодії тягача і причепа при гальмуванні
Теоретичні відомості Дослідження динаміки процесу взаємодії розглянемо для розрахункової схеми, показаної на рис.2.1
Ланки поїзда мають пружну беззазорне зчеплення з коефіцієнтами жорсткості С і опору S. Маса тягача М1; маса причепа М2. При розробці розрахункової схеми із всіх діючих сил враховуються лише ті схеми із всіх діючих сил враховуються лише ті, які здійснюють найбільш суттєвий вплив на динаміку гальмування поїзда. В даній задачі такими є сили опору Q1 на колесах тягача і Q2 на колесах причепу, що включає в себе сили опору руху і гальмові сили. Приймається, що поїзд рухається по рівній горизонтальній поверхні; перерозподіл ваги ланок по осям не враховується. В цьому випадку сили, що діють в колесах осей ланок, можна замінити сумарними силами на ланках. Гальмова система причепа починає спрацьовувати на час T0 раніше часу спрацювання гальмі тягача T1. Для прийнятої розрахункової схеми узагальнені координати запишуться: · Для центру ваги системи:
· Відносно переміщення ланок поїзда:
де х1,х2 – координати центрів ваги ланок. Система диференційних рівнянь, що описують рух поїзда, буде:
Гальмові зусилля на колесах ланок прикладаємо по лінійному закону:
де
Інші позначення на рис.1. Сила в зчепленні Ркр=С·q+S·q2 при деформації пружного елемента, тобто коли ׀D׀ – гранична деформація пружного елемента (хід зчеплення) при жорсткому упорі один в одному передаючих ланок зчеплення. При виборі пружної деформації, коли
Іп – причеп. Заміною змінних
з початковими умовами (масив W):
де V0 — максимально допустима швидкість автопоїзда перед початком гальмування. Важливою характеристикою гальмівних властивостей автопоїзда є гальмівний шлях
Початкові дані:
· початкова маса тягачя M1=7,2 т · повна маса причепа М2=10 т · жорсткість зчіпного пристрою С=56800 Н/м · коефіцієнт опору в зчіпці S=2500 · коефіцієнт опору руху Z=0,04 · коефіцієнт зчіплення Z1=0,65 · час спрацювання гальм тягача T1=1,2 с · час випередження спрацювання гальм причепа Т0=0,4 с · швидкість руху поїзда перед початком гальмування V0=9 м/с · відстань між центрами мас ланок перед гальмуванням q2=3 м · час наростання сил опору – тягача Т2=0,4 с – причепа Т3=0,5 с · пружний хід зчіпки D=0,03 м t= T1+T0 t= 0,01…1,6 Розв’язок Гальмові зусилля на колесах ланок, що прикладаються по лінійному закону визначаються за формулою:
{
де Т2=Т3-Т1; t – час спрацювання.
Зобразимо залежність гальмових зусиль на колесах від часу спрацювання t: Q1 (t), Q2 (t).
Визначимо сповільнення автопоїзда:
де Jа—сповільнення тягача Jn—сповільнення причепа
Побудуємо залежність сповільнення автопоїзда від часу
Формула визначення зусилля в зчіпці:
Побудуємо залежність зусилля в зчіпці від часу спрацювання:
Порядок виконання роботи 1. Вивчити: а) взаємодія тягача і причепа при гальмуванні; б) методику дослідження динаміки процесу взаємодії тягача і причепа при гальмуванні. 2. Записати: а) вихідні дані; б) текст програми в) результати проведених розрахунків. г) зробити висновки Контрольні запитання 1. Вимоги до гальмових систем автопоїздів. 2. Динамічна характеристика гальмової системи. 3. Сили, які діють на тягач і причеп при гальмуванні. 4. Стійкість автопоїзда при гальмуванні. 5. Характеристики гальмування. 6. Гальмові приводи автопоїздів. 7. Особливості конструкції основних елементів гальмових систем автопоїздів. 8. Гальма-сповільнювачі. Варіанти завдань
Текст програми
10 REM: ВЗАИМОДЕЙСТВИЕ ТЯГАЧА: 20 REM: С ПРИЦЕПОМ ПРИ ТОРМОЖЕНИИ: 30 PRINT "**** ВВЕДИТЕ ****" 40 PRINT "ШАГ ВЫЧИСЛЕНИЙ {H}" 50 INPUT H 60 DIM W(4), Y(4), K(2), F(4), A(200) 70 LET N = 4 80 REM: ** НАЧАЛЬНЫЕ ЗНАЧЕНИЯ **: 90 DATA 0,8.4,3,0 100 READ W(1), W(2), W(3), W(4) 110 REM ** ВВОД КОНСТАНТ ** 120 DATA 3200,5470,56800,2500 130 READ M1, M2, M3 140 DATA 4.00000E-02,.65,1.2,.4,2,2.2 150 READ Z, z1, T1, T0, T3, T4 160 REM ** РЕШЕНИЕ СИСТЕМЫ ДИФФ. УРАВНЕНИЯ ** 170 REM ** МЕТОДОМ РУНГЕ - КУТТА ** 180 LET X = T1 - T0 190 REM 200 FOR j = 1 TO N 210 LET Y(j) = W(j) 220 NEXT j 230 LET A(1) = Y(3) 240 LET J1 = 1 250 GOSUB 650 260 FOR j = 1 TO N 270 LET U = H * F(j) 280 LET K(j) = U 290 LET Y(j) = W(j) + U / 2 300 NEXT j 310 LET X = X + H / 2 320 GOSUB 650 330 FOR j = 1 TO N 340 LET U = H * F(j) 350 LET K(j) = K(j) + U * 2 360 LET Y(j) = W(j) + U / 2 370 NEXT j 380 GOSUB 650 390 FOR j = 1 TO N 400 LET U = H * F(j) 410 LET K(j) = K(j) + U * 2 420 LET Y(j) = W(j) + U 430 NEXT j 440 LET H = H + H / 2 450 PRINT "ДЛЯ X="; X 460 GOSUB 650 470 FOR j = 1 TO N 480 LET Y(j) = W(j) + (K(j) + H * F(j)) / 6 490 PRINT "Y("; j; ")="; Y(j) 500 LET W(j) = Y(j) 510 NEXT j 520 REM ** ОПРЕДЕЛЕНИЕ УСИЛИЯ В СЦЕПКЕ ** 530 LET J1 = J1 + 1 540 LET J2 = J1 - 1 550 LET A(J1) = W(3) 560 LET D9 = A(J1) - A(J2) 570 IF ABS(D9) >.03 GOTO 600 580 LET S7 = C * D9 + S * W(4) 590 GOTO 610 600 LET S7 = 2 * (M1 * (Q2 + Q4 * Z) - M2 * (Q1 + Q3 * Z)) / (M1 + M2) 610 PRINT " УСИЛИЕ В СЦЕПКЕ F12= "; S7; " H " 620 IF X > 2 GOTO 900 630 GOTO 250 640 REM================================== 650 REM Q^ | 660 REM | *---------Q2 | 670 REM | /| *-------Q1 | 680 REM | / |/| | 690 REM | / | | | 700 REM | / /| | | 710 REM | / / | | | 720 REM | / / | | | 730 REM +==*==*===*=*==========> T | 740 REM T1 T4 T3 | 750 REM================================== 760 LET Q3 = 9.81 * M1 770 LET Q4 = 9.81 * M2 780 LET Q1 = Q3 * (z1 - Z) * (X - T1) / (T3 - T1) + Q3 * Z 790 LET A = T1 - T0 800 LET Q2 = Q4 * (z1 - Z) * (X - A) / (T4 - A) + Q4 * Z 810 LET F(1) = Y(2) 820 LET F(3) = Y(4) 830 IF X > T1 GOTO 850 840 LET Q1 = 0 850 LET F(2) = -(Q1 + Q2) / (M1 + M2) 860 LET G = -Q1 / M1 + Q2 / M2 870 LET M = M1 + M2 880 LET F(4) = G - M * (C * Y(3) + S * Y(4)) / (M1 * M2) 890 RETURN 900 END
Лабораторна робота № 3
ДОСЛІДЖЕННЯ ПОКАЗНИКІВ МАНЕВРЕНОСТІ СПЕЦІАЛІЗОВАНИХ АВТОМОБІЛІВ ТА АВТОПОЇЗДІВ
Мета роботи: Набути навиків побудови основної траєкторії криволінійного руху автомобілів, отримати необхідні знання для використання даного матеріалу на практиці. Теоретичні відомості Кінематика криволінійного руху. Маневреність автопоїздів оцінюється залежностями, що випливають з кінематики їхнього криволінійного руху. При цьому приймається, що опорна поверхня, по якій відбувається криволінійний рух автопоїзда, горизонтальна і має покриття, що не створює опору рухові. Відведення коліс не враховується, що значно спрощує розрахунки і забезпечує прийнятну точність для практичних цілей. На рис. 3.1 показані основні траєкторії, повороту автопоїзда на 90 і 180° і при маневрі типу „переставка”
а) б) в)
Рисунок 3.1 - Форми основних траєкторій криволінійного руху автопоїзда при його повороті: а) – на 90°; б) – на 180°; в) – при маневрі типу „переставка”
При аналізі кінематики криволінійного руху автопоїзда визначають траєкторії відповідних його точок. Із траєкторій виділяють основну, якою є траєкторія середини ведучого моста (одновісна ланка) або середини центра двовісного візка (двовісна ланка). Перехідні криві основних траєкторій представляють криві типу радіальної спіралі, що описуються параметричними рівняннями:
де Режимний параметр
де Колова ділянка траєкторії має радіус
В формулах (3.3) значення Центральний кут
Якщо кругової ділянки на основній траєкторії немає, допустимий мінімальний радіус основної траєкторії руху автопоїзда
Проекції основної траєкторії руху автопоїзда на осі координат характеризують довжину і ширину криволінійної траєкторії. В загальному вигляді довжина криволінійної траєкторії
Відрізок
Якщо
Ширина криволінійної траєкторії в загальному випадку
При маневрі автопоїзда типу „переставка” (рис. 3.1, в) координати центра кругової ділянки
де Значення Крім основної траєкторії, необхідно знати траєкторії будь-яких точок автомобіля. Координати будь-якої точки автомобіля на вхідній траєкторії (рис. 3.2)
Рисунок 3.2 - Схеми для визначення радіусів і координат траєкторій будь-якої точки руху автомобіля-тягача (а – на вході в поворот, б – при руху по дузі кола)
Для кругового руху зручніше визначати не координати заданої точки, а її радіус
Радіус передньої габаритної точки автомобіля
де Радіус задньої габаритної точки автомобіля
де Габаритна смуга руху. Габаритна смуга руху автопоїзда є площа опорної поверхні, обмежена проекціями траєкторій габаритних точок, які являються зовнішньою та внутрішньою по відношенню до миттєвого центра кривизни повороту автопоїзда. Габаритна смуга руху формується основною траєкторією та зсувом При круговому русі автопоїзда ширина габаритної смуги руху:
де Для автопоїздів при круговому повороті
Де Передаточні відношення прямого зв’язку
де Коли вісь напівпричепа розташована біля основи перпендикуляра, опущеного з центра
де
Рисунок 3.3 - Схема кругового руху сідельного автопоїзда з довго базовим напівпричепом при різному співвідношенні бази і заднього звісу та при різному передаточному відношенні
Зсув траєкторії основної точки напівпричепа
Коли вісь напівпричепа розташована так, що радіус
де При цьому для вписування напівпричепа в габаритну смугу руху автомобіля тягача при
Ширина кругової габаритної смуги руху для варіанта при керованому напівпричепі
Якщо звіс дуже великий та напівпричіп керований, необхідно визначити також радіус повороту задньої габаритної точки
Цей вираз дійсний при
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 359; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.112 (0.008 с.) |


 (2.1)
(2.1) , (2.2)
, (2.2) (2.3)
(2.3) (2.4)
(2.4)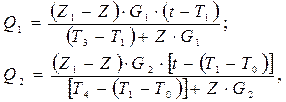 (2.5)
(2.5) – коефіцієнти опору коченню і зчеплення;
– коефіцієнти опору коченню і зчеплення; – вага тягача і причепа;
– вага тягача і причепа; , де ∆q – деформація пружного елемента;
, де ∆q – деформація пружного елемента; зусилля в зчіпному механізмі:
зусилля в зчіпному механізмі: (2.6)
(2.6) сповільнення тягача
сповільнення тягача зводимо систему рівнянь до системи першого порядку:
зводимо систему рівнянь до системи першого порядку: (2.7)
(2.7) (2.8)
(2.8) , який можна поділити на дві складові: шлях, пройдений від початку гальмування до повної зупинки автопоїзда, і шлях, пройдений автопоїздом за час реакції водія:
, який можна поділити на дві складові: шлях, пройдений від початку гальмування до повної зупинки автопоїзда, і шлях, пройдений автопоїздом за час реакції водія: (2.9)
(2.9) - коефіцієнт, що характеризує умови експлуатації (тип привода гальм);
- коефіцієнт, що характеризує умови експлуатації (тип привода гальм);
 ,
,






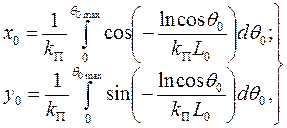 (3.1)
(3.1) – кут повороту середнього приведеного керованого колеса автомобіля-тягача;
– кут повороту середнього приведеного керованого колеса автомобіля-тягача;  – база автомобіля-тягача;
– база автомобіля-тягача; 
 – режимний параметр, що характеризує режим криволінійного руху.
– режимний параметр, що характеризує режим криволінійного руху. (3.2)
(3.2) – кутова швидкість повороту середнього приведеного колеса автомобіля-тягача;
– кутова швидкість повороту середнього приведеного колеса автомобіля-тягача;  – швидкість поступального руху автопоїзда.
– швидкість поступального руху автопоїзда. . Координати центра кругової ділянки:
. Координати центра кругової ділянки: (3.3)
(3.3) ,
,  ,
,  і
і  відповідають положенню автомобіля в точці 1.
відповідають положенню автомобіля в точці 1. (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) в загальному випадку, тобто при
в загальному випадку, тобто при  і
і  ,
, (3.7)
(3.7) ,
, (3.8)
(3.8) (3.9)
(3.9) на вході визначаються по формулі (3.3), а центр кругової ділянки
на вході визначаються по формулі (3.3), а центр кругової ділянки  на виході має наступні координати:
на виході має наступні координати: (3.10)
(3.10) .
. і
і  ;
;  , а на вихідній траєкторії в цих формулах замість значення кута
, а на вихідній траєкторії в цих формулах замість значення кута  підставляється значення різниці кутів
підставляється значення різниці кутів  . При цьому
. При цьому  – відстань від основної точки М до заданої точки уздовж подовжньої осі – береться зі знаком плюс, якщо точка розташована попереду по ходу руху, і зі знаком мінус – якщо точка розташована позаду;
– відстань від основної точки М до заданої точки уздовж подовжньої осі – береться зі знаком плюс, якщо точка розташована попереду по ходу руху, і зі знаком мінус – якщо точка розташована позаду;  відстань від заданої точки до подовжньої осі автомобіля.
відстань від заданої точки до подовжньої осі автомобіля.
 . (3.11)
. (3.11) (3.12)
(3.12) – габаритна ширина автомобіля;
– габаритна ширина автомобіля;  – передній звіс.
– передній звіс. (3.13)
(3.13) – задній звіс.
– задній звіс. траєкторій причіпних ланок від основної.
траєкторій причіпних ланок від основної. (3.14)
(3.14) – радіус повороту ведучої точки автомобіля-тягача;
– радіус повороту ведучої точки автомобіля-тягача;  – габаритна ширина самої широкої причіпної ланки;
– габаритна ширина самої широкої причіпної ланки;  – зсув траєкторії основної точки (середини заднього моста) замикаючої причіпної ланки по відношенню до основної траєкторії.
– зсув траєкторії основної точки (середини заднього моста) замикаючої причіпної ланки по відношенню до основної траєкторії. , (3.15)
, (3.15) – коефіцієнт, що визначається в залежності від типу транспортної ланки та наявності некерованих коліс або осей (ланка першого роду) та керованих коліс або осей (ланка другого роду);
– коефіцієнт, що визначається в залежності від типу транспортної ланки та наявності некерованих коліс або осей (ланка першого роду) та керованих коліс або осей (ланка другого роду);  – довжина бази двохвісного причепа.
– довжина бази двохвісного причепа. та зворотного зв’язку
та зворотного зв’язку 
 ; (3.16)
; (3.16) ; (3.17)
; (3.17) – кут складання;
– кут складання;  – кут між вертикальною площиною середнього поворотного колеса даної ланки причепа та повздовжньої вертикальної площини симетрії спряженої ланки;
– кут між вертикальною площиною середнього поворотного колеса даної ланки причепа та повздовжньої вертикальної площини симетрії спряженої ланки;  – кут між повздовжніми осями ланок двохосного причепа.
– кут між повздовжніми осями ланок двохосного причепа. (рис. 3.3) на повздовжню вісь напівпричепа, вписуємість напівпричепа в габаритну смугу руху автомобіля-тягача забезпечена при умові, що заданій звіс напівпричепа
(рис. 3.3) на повздовжню вісь напівпричепа, вписуємість напівпричепа в габаритну смугу руху автомобіля-тягача забезпечена при умові, що заданій звіс напівпричепа , (3.18)
, (3.18) – радіус зовнішнього габаритного кола, що описується автомобілем-тягачем;
– радіус зовнішнього габаритного кола, що описується автомобілем-тягачем; 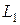 – довжина бази одновісного причепа;
– довжина бази одновісного причепа; 
 . (3.19)
. (3.19) траєкторії середини менше радіуса повороту
траєкторії середини менше радіуса повороту  (3.20)
(3.20) ;
;  – кут складання;
– кут складання;  – кут між вертикальною площиною середнього поворотного колеса напівпричепа і повздовжньою вертикальною площиною симетрії тягача.
– кут між вертикальною площиною середнього поворотного колеса напівпричепа і повздовжньою вертикальною площиною симетрії тягача. заданий звіс напівпричепа
заданий звіс напівпричепа (3.21)
(3.21) (3.22)
(3.22) :
: (3.23)
(3.23) , то ширина габаритної смуги руху автопоїзда
, то ширина габаритної смуги руху автопоїзда (3.24)
(3.24)


