Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зведення відкритої Т-задачі до закритої Т-задачіСодержание книги
Поиск на нашем сайте
Випадок, коли сумарна наявність вантажів дорівнює сумарному обсягу замовлень, тобто при виконанні умови Оскільки методи розв’язання Т-задач передбачають саме закриту Т-задачу, у випадку наявності відкритої Т-задачі її необхідно привести до закритої. У випадку, коли У випадку, коли Отримана таким чином закрита (збалансована) Т-задача вирішується будь-яким з зазначених методів.
Пошук оптимального рішення Т-задачі у середовищі “EXCEL”
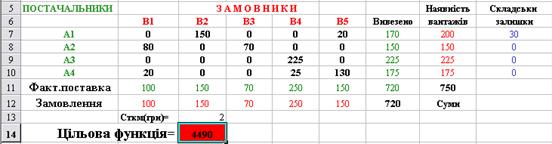
Можливо отримання також оптимального плану перевезень у середовищі “EXCEL”. На листі електронної таблиці EXCEL, що наведено на рис. 3.1, показаний приклад розміщення початкових даних. Після цього слідує ввести необхідні розрахункові формули в певні клітинки електронної таблиці. В клітинки B11…F11 вносяться формули: (= СУММ(B7:B10)... (= СУММ(F7:F10). В клітинки G7…G10 вносяться формули: =СУММ(B7:F7)... (=СУММ(B10:F10). В клітинку оптимального рішення (С14) вводимо формулу: (=СУММПРОИЗВ(B1:F4;B7:F10)*C13)
Рис. 3.1. Приклад введення даних транспортної задачи в електронну таблицю “EXCEL”.
Пошук оптимального рішення здійснюється за допомогою опції Поиск решения(Меню “Сервис”). Для розв’язання Т - задачі вводимо необхідні обмеження (див. рис. 3.2). Результат рішення (оптимальний план перевезень) представлено на рис. 3.3. Загальні витрати на виконання оптимального плану перевезень становитимуть 4490 грн. (див. клітинку С14).
Рис. 3.2. Введення обмежень Т-задачі
Рис. 3.3. Результат рішення Т-задачі ЛАБОРАТОРНА РОБОТА № 4. ОСНОВНІ СПОСОБИ ЗВЕДЕННЯ МЕРЕЖЕВОЇ ЗАДАЧІ ДО МАТРИЧНОЇ ФОРМИ ЗАВДАННЯ ДО ЛАБОРАТОРНОЇ РОБОТИ 1. Розв'язати мережеву ТЗ без обмежень на пропускні здатності за допомогою Excel-таблиці, одержати оптимальний план перевезень за допомогою “EXCEL -2003”. Проаналізувати результати. 2. Розв'язати мережеву ТЗ з обмеженнями на пропускні здатності за допомогою Excel-таблиці, одержати оптимальний план перевезень за допомогою “EXCEL -2003”. Проаналізувати результати. ВАРІАНТИ ЗАВДАНЬ
Додати до транспортної мережі без обмежень на пропускні здатності (рис. 4.1) та транспортної мережі з обмеженнями на пропускні здатності замовлень (рис. 4.2)один пункт постачання з обсягом 5 одиниць вантажу, один пункт споживання з обсягом 5 одиниць вантажу та один проміжний транспортний пункт.
МЕТОДИЧНІ ВКАЗІВКИ ДО ВИКОНАННЯ ЛАБОРАТОРНОЇ РОБОТИ На рис. 4.1 зображена мережа з 7 вершинами і 11 ланками. Поруч із відповідною вершиною у дужках числом зі знаком плюс показаний обсяг виробництва, а обсяг споживання, відповідно, числом зі знаком мінус. Вартість перевезення вантажу вписана в кожну дугу. Також на рис. 4.1 подані розподіли вантажопотоків і потенціалів.
Рис. 4.1. Приклад ТМ без Рис. 4.2. Приклад ТМ з обмежень на пропускні здатності обмеженнями на пропускні здатності Перший спосіб – Ордена А. показаний у табл. 4.1. Кожній вершині мережі виділяється рядок і стовпець. Таким чином у нашому випадку, таблиця складається із семи рядків і семи стовпців. Вона завжди повинна бути квадратною. У клітинках головної діагоналі таблиці 4.1, 2.2 і т. д. вартість перевезення дорівнює 0, тому що вихідних і одночасно вхідних дуг до тієї самої вершини бути не може. Для вершин, з'єднаних між собою ланкою, у клітинках таблиці на перетинанні відповідних рядків і стовпців проставлена вартість транспортування цією ланкою. Інші клітинки заблоковані більшими, порівняно з вартостями перевезень, числами (у табл. 4.1 це незаповнені клітинки). Для зручності розрахунку до значення обсягу виробництва (споживання) до кожної вершини додається яке-небудь позитивне число. У табл. 4.1 це число 9. Таким чином, обсяг виробництва у вершині 1 буде 7+9=16, у транзитній вершині 2 – 9, так само як і обсяг споживання і т. д. Потім ТЗ розв'язують будь-яким відомим методом. У табл. 4.1 показаний остаточний результат рішення задачі – значення оптимального плану перевезень вантажу виділені курсивом, а на рис. 4.3 – результат розв'язання за допомогою Excel-таблиці. Таблиця 4.1
|
|||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 291; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |

 , відповідає так званої закритої (збалансованої) Т-задачі. При
, відповідає так званої закритої (збалансованої) Т-задачі. При  Т-задача є відкритою (незбалансованою).
Т-задача є відкритою (незбалансованою). (попит перевищує пропозицію), вводиться додатковий (m+1)-й постачальник, що має фіктивну наявність вантажу
(попит перевищує пропозицію), вводиться додатковий (m+1)-й постачальник, що має фіктивну наявність вантажу 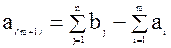 , а відстані від цього постачальника до кожного з замовників (або вартість перевезення одиниці вантажу) приймаються рівними нулю.
, а відстані від цього постачальника до кожного з замовників (або вартість перевезення одиниці вантажу) приймаються рівними нулю. (пропозиція перевищує попит), вводиться додатковий (n+1)-й замовник, що замовляє фіктивну кількість вантажу
(пропозиція перевищує попит), вводиться додатковий (n+1)-й замовник, що замовляє фіктивну кількість вантажу  , а відстані від цього замовника до усіх постачальників приймаються рівними нулю.
, а відстані від цього замовника до усіх постачальників приймаються рівними нулю.