
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методом північно-західного кутаСодержание книги Поиск на нашем сайте
Із застосуванням транспортних таблиць Т-задача формулюється наступним чином: визначити такі позитивні значення обсягів перевезень Як вже визначалось, починаємо завжди зі складання опорного плану перевезень. Розглянемо найбільш поширений метод складання опорного плану, що зветься методом північно – західного кута. Згідно таблиці 4 маємо: m = 3; n = 4. b1 = 80 т.; b2 = 100 т.; b3 = 110 т.; b4 = 70 т.; а1 = 100 т.; а2 = 120 т.; а3 = 140 т.; Заповнення обсягів перевезень починаємо з клітинки Для розглянутого випадку робимо наступне: 1. Задовольнимо 2. Оскільки 3. Щоб повністю задовольнити Підрахуємо кількість ненульових перевезень (зайнятих клітинок). Таких є 6, що відповідає обов'язкової умові (n + m – 1) = (4 + 3 – 1) = 6. Оскільки суми перевезень по рядах і колонках відповідають
Після складання опорного плану стає питання, чи є цей план перевезень оптимальним? Скоріше за все ні, тому що ми не звертали уваги на існуючі відстані від Нехай опорний план, отриманий за допомогою методу північно-західного кута, є такий, що наведено в таблиці 1.4. Простежимо, як буде змінюватися план перевезень (якщо він не є оптимальним) з оцінкою кожного разу поточного значення загальної вартості перевезень. Найвірогідніше, що ця вартість має поступово зменшуватися за рахунок поліпшення плану перевезень. Перевіряємо, чи зміниться в бік зменшення вартості план перевезень, якщо почергово робити спробу перемістити одиницю вантажу в кожну незайняту клітинку. В цьому випадку кожну незайняту клітинку помістимо у вершину контуру, в інших вершинах якого розташовані зайняті клітинки. Наприклад, для незайнятої клітинки Для кожного такого контуру знаходимо вартісну характеристику переміщення одиниці вантажу в незайняту клітинку (
Іншими словами, переміщення одиниці вантажу (або будь-якого об’єму) по контуру Очевидно, що якщо отримане значення Визначаємо
α31 = 9 – 4 + 7 – 6 + 1 – 6 = 1; Таким чином, доцільно перерозподілити обсяги перевезень базового плану по контуру Об’єм вантажу, що переміщається, визначається як мінімальний з від’ємних об’ємів по даному контуру ( Очевидно, що загальна вартість перевезень повинна при цьому змінитися на:
і має бути рівною
Щоб перевірити скоректований план на оптимальність, будуємо таблицю 3.4, що аналогічна таблиці 3 для отримання нового плану, і знову перевіряємо його на оптимальність з допомогою вартісних характеристик незайнятих клітинок.
Для отриманого плану перевезень маємо:
Перевіряємо загальну вартість перевезень:
Таблиця 3.4
що співпадає з очікуваною вартістю перевезень. Але цей план не є також оптимальним, так як
Нагадаємо, що план буде оптимальним в тому випадку, якщо всі вартісні характеристики незаповнених клітинок будуть невід’ємними ( Більш простим методом оптимізації плану перевезень є метод потенціалів, суть якого полягає у наступному. 1. Приймаємо будь-який початковий потенціал ui для i-го ряду таблиці; шукаємо заповнену клітинку (ij), для якої і визначаємо відповідний потенціал та рахуємо: vj = lij - ui. Робимо аналогічні розрахунки для решти рядів і колонок таблиці, спираючись на вже розраховані транспортні потенціали.
Таблиця 3.5
2. Після визначення 3. Якщо у будь якій незайнятій клітинці При умові Наприклад, є певний опорний план перевезень (табл. 3.6). Розрахуємо потенціали Приймаємо
Відмітимо, що для отриманого плану (при C = 1 грн/ткм) маємо L = 980 грн, що набагато краще опорного плану, отриманого за методом північно-західного кута (L1=1540 грн.). Перевіряємо опорний план на оптимальність, використовуючи отримані потенціали. Для цього перевіряємо умову оптимальності для всіх незайнятих клітинок плану, тобто
Опорний план не є оптимальним, тому що для клітинки
Таблиця 3.6
Для цього шукаємо контур, що містить у решті кутів зайняті клітинки. Це контур:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 270; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.104.36 (0.008 с.) |

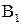









 +
+

 , сума яких по кожному і –му ряду (
, сума яких по кожному і –му ряду ( ) дорівнює
) дорівнює  ) дорівнює
) дорівнює  ) по всіх клітинках буде мінімальною.
) по всіх клітинках буде мінімальною. (звідси назва методу). Принцип заповнення: задовольнити максимально можливий обсяг замовлення
(звідси назва методу). Принцип заповнення: задовольнити максимально можливий обсяг замовлення  ; якщо обсягу
; якщо обсягу  не вистачає, беремо частину від
не вистачає, беремо частину від  , якщо в
, якщо в  і т.д.
і т.д. , решту
, решту 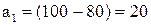 відправимо до B2;
відправимо до B2;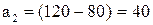 відправимо до
відправимо до  (ще 70). Решту
(ще 70). Решту 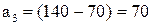 відправимо до
відправимо до  (
(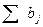 (
(
 до
до  , що значно відрізняються одна від одної.
, що значно відрізняються одна від одної. таким контуром буде:
таким контуром буде:  .
. ), не змінюючи баланс сум перевезень в рядках та стовпчиках. Для переміщення, наприклад, 1 т вантажу в
), не змінюючи баланс сум перевезень в рядках та стовпчиках. Для переміщення, наприклад, 1 т вантажу в  ), але для збереження балансу вантажів в рядках і стовпчиках зменшуємо на 1 т вантаж в клітинці
), але для збереження балансу вантажів в рядках і стовпчиках зменшуємо на 1 т вантаж в клітинці  , що викличе зменшення вартості перевезень на (
, що викличе зменшення вартості перевезень на ( ). Оскільки
). Оскільки  зменшується на 1 т, додамо в клітинку
зменшується на 1 т, додамо в клітинку 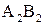 також 1 т, що викличе збільшення вартості перевезення на (
також 1 т, що викличе збільшення вартості перевезення на ( ). Однак збільшення
). Однак збільшення  на 1 т повинно призвести до зменшення
на 1 т повинно призвести до зменшення  на 1 т, тобто до зменшення вартості перевезень на (
на 1 т, тобто до зменшення вартості перевезень на (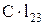 ). Це зменшення
). Це зменшення 
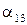 як додатній коефіцієнт при алгебраїчній сумі відстаней по даному контуру, тому будемо визначати
як додатній коефіцієнт при алгебраїчній сумі відстаней по даному контуру, тому будемо визначати  в незайнятій (ij)-ї клітинці як алгебраїчну суму відстаней по даному контуру, причому для даної незайнятої клітинки ця відстань приймається завжди зі знаком “+”, потім за мірою просування по контуру (або в одну, або в іншу сторону – напрям проходження контуру не має значення) відстані
в незайнятій (ij)-ї клітинці як алгебраїчну суму відстаней по даному контуру, причому для даної незайнятої клітинки ця відстань приймається завжди зі знаком “+”, потім за мірою просування по контуру (або в одну, або в іншу сторону – напрям проходження контуру не має значення) відстані  приймають послідовно знаки “-” або “+”.
приймають послідовно знаки “-” або “+”.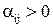 , то переміщення в цю точку збільшується вартість перевезень; якщо
, то переміщення в цю точку збільшується вартість перевезень; якщо  , то вартість перевезень не змінюється.
, то вартість перевезень не змінюється. ;
; 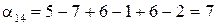
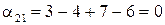 ;
; 

 з метою завантаження клітинки
з метою завантаження клітинки  , яка має
, яка має  . Будуємо цей контур з виказанням знаків, що послідовно міняються і позначають додавання або зменшення об’ємів перевезень по даному контуру (див. табл. 3.4).
. Будуємо цей контур з виказанням знаків, що послідовно міняються і позначають додавання або зменшення об’ємів перевезень по даному контуру (див. табл. 3.4). ). Таким чином, переміщення вантажу
). Таким чином, переміщення вантажу  по даному контуру дозволить максимально завантажити клітинку
по даному контуру дозволить максимально завантажити клітинку  . Очевидно, що при цьому
. Очевидно, що при цьому  ;
;  .
.

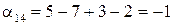

 ;
; 
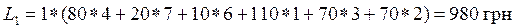 .
.
 -
-
 +
+
 +
+
 , тому будуємо замкнутий контур для клітинки
, тому будуємо замкнутий контур для клітинки  , що має
, що має  в клітинку
в клітинку  , а загальна вартість
, а загальна вартість , і т.д.
, і т.д. ). Після цього процес пошуку оптимального плану перевезень завершено. Зокрема для даного плану оптимальним буде наступний план перевезень, який має Lопт=950 грн. Цей метод оптимізації має назву розподільчий.
). Після цього процес пошуку оптимального плану перевезень завершено. Зокрема для даного плану оптимальним буде наступний план перевезень, який має Lопт=950 грн. Цей метод оптимізації має назву розподільчий.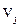 i
i  (
( для всіх (ij) незайнятих клітинок таблиці (тобто для
для всіх (ij) незайнятих клітинок таблиці (тобто для  ). Якщо ця нерівність має місце для усіх без виключення незайнятих клітинок, план перевезень є оптимальним.
). Якщо ця нерівність має місце для усіх без виключення незайнятих клітинок, план перевезень є оптимальним. , то складений план перевезень не є оптимальним і підлягає корегуванню. Корегування полягає в заповненні незайнятих клітинок, що мають
, то складений план перевезень не є оптимальним і підлягає корегуванню. Корегування полягає в заповненні незайнятих клітинок, що мають  для незайнятої клітинки (
для незайнятої клітинки ( .
. , тоді
, тоді  ;
; 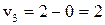 . Використовуючи вже отримані потенціали, визначаємо решту потенціалів:
. Використовуючи вже отримані потенціали, визначаємо решту потенціалів: ;
;  ;
; ;
; 
 ;
;  ;
;  ;
; ;
;  ;
;  .
.
 . Це означає, що ця клітинка, як кажуть, є потенційною і має бути завантажена.
. Це означає, що ця клітинка, як кажуть, є потенційною і має бути завантажена.



 +
+
 3
+
3
+
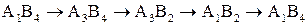 . Оскільки ми завантажуємо
. Оскільки ми завантажуємо  і дорівнює x = 30 т. Пересуваємо цей обсяг по контуру з урахуванням знаків і отримуємо новий план перевезень. Далі процес повторюється до отримання оптимального плану.
і дорівнює x = 30 т. Пересуваємо цей обсяг по контуру з урахуванням знаків і отримуємо новий план перевезень. Далі процес повторюється до отримання оптимального плану.


