
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение усилий в элементах фермы.Содержание книги Поиск на нашем сайте
Принимаем стальную стропильную ферму трапецеидального очертания с уклоном верхнего пояса 1/10 из спаренных стальных горячекатаных профилей, соединенных в узлах фасонками. Высоту фермы принимаем унифицированной равной – на опоре 2,2 м, в середине пролета 3,1 м. по осям (см. рис. 1). Усилия в стержнях фермы находим с помощью программного комплекса ПК «Лира 9.6». Найденные усилия в стержнях заносим в таблицу 2. Таблица 2. Усилия в стержнях фермы.
Подбор сечений. Фасонки принимаем t=14 мм в зависимости от усилия в опорном раскосе N=-662,931кН Верхний пояс 8,17,9,16: Расчётное усилие: N= -612,639 кН. Задаёмся гибкостью λ=80; Коэффициент продольного изгиба при λ=80 для стали С245 с Ry=24кН/см2 φ=0.686.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟110×8. Характеристики: А∟=17,2; Jx=198см4; ix=3,39см; iy=4,87см; z0=3см. Площадь двух уголков: Определяем λx, λy:
φmin при гибкости λx=44,45: φmin=0.875 Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элементов 8,17,9,16 из ∟110×8. Верхний пояс 10,11,14,15: Расчётное усилие: N= -875,199 кН. Задаёмся гибкостью λ=80; Коэффициент продольного изгиба при λ=80 для стали С245 с Ry=24кН/см2, φ=0.686.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟125×10. Характеристики: А∟=24,3см2; Jx=360см4; ix=3,85см; iy=5,52см; z0=3,45см. Площадь двух уголков: Определяем λx, λy:
φmin при гибкости λx=39,14: φmin=0,897 Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элементов 10,11,14,15 из ∟125×10. Верхний пояс 12,13: Расчётное усилие: N= -889,315 кН. Задаёмся гибкостью λ=80; Коэффициент продольного изгиба при λ=80 для стали С245 с Ry=24кН/см2, φ=0.686.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟125×10. Характеристики А∟=24,3см2; Jx=360см4; ix=3,85см; iy=5,52см; z0=3,45см Площадь двух уголков: Определяем λx, λy:
φmin при гибкости λx=39,14: φmin=0,897 Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элементов 12,13 из ∟125×10.
Нижний пояс 6,1: Расчётное усилие: N=356,68кН.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟70×6. Характеристики: А∟=8,15см2; Jx=37,6см4; ix=2,15см; iy=3,25см; z0=1,94см. Площадь двух уголков: Определяем λx, λy:
Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 6,1 из ∟70×6. Нижний пояс 2,5: Расчётное усилие: N=776,376кН.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟110×8. Характеристики: А∟=17,2см2; Jx=198см4; ix=3,39см; iy=4,87см; z0=3см. Площадь двух уголков: Определяем λx, λy:
Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 2,5 из ∟110×8. Нижний пояс 3,4: Расчётное усилие: N=904,066кН.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟125×9. Характеристики: А∟=22см2; Jx=327см4; ix=3,86см; iy=5,48см; z0=3,4см. Площадь двух уголков: Определяем λx, λy:
Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 3,4 из ∟125×9. Раскос 26,37: Расчётное усилие: N= -662,931кН. Задаёмся гибкостью λ=80; Коэффициент продольного изгиба при λ=80 для стали с Ry=24кН/см2 φ=0.686.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟125×9. Характеристики: А∟=22см2; Jx=327см4; ix=3,86см; iy=5,48см; z0=3,4см Площадь двух уголков: Определяем λx, λy:
φmin при гибкости λx=72: φmin=0.740 Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 26,37 из ∟125×9 Раскос 27,36: Расчётное усилие: N=470,078кН.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟75×8. Характеристики: А∟=11,5см2; Jx=59,8см4; ix=2,28см; iy=3,5см; z0=2,15см. Площадь двух уголков: Определяем λx, λy:
Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 27,36 из ∟75×8. Раскос 28,35: Расчётное усилие: N= -338,566кН. Задаёмся гибкостью λ=80; Коэффициент продольного изгиба при λ=80 для стали с Ry=24кН/см2 φ=0.686.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟90×7. Характеристики: А∟=12,3см2; Jx=94,3см4; ix=2,77см; iy=4,06см; z0=2,47см. Площадь двух уголков: Определяем λx, λy:
φmin при гибкости λx=87,8: φmin=0,628 Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 28,35 из ∟90×7 Раскос 29,34: Расчётное усилие: N=191,799кН.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟56×4. Характеристики: А∟=4,38см2; Jx=13,1см4; ix=1,73см; iy=2,66см; z0=1,52см. Площадь двух уголков: Определяем λx, λy:
Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 29,34 из ∟56×4.
Раскос 30,33: Расчётное усилие: N= -107,441кН. Задаёмся гибкостью λ=80; Коэффициент продольного изгиба при λ=80 для стали с Ry=24кН/см2 φ=0.686.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем прокат: ∟75×5. Характеристики: А∟=7,39см2; Jx=39,5см4; ix=2,31см; iy=3,42см; z0=2,02. Площадь двух уголков: Определяем λx, λy:
φmin при гибкости λx=114,61: φmin=0,450 Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 30,33 из ∟75×5 Раскос 31,32: Расчётное усилие: N=-83,6825
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟75×5. Характеристики: А∟=7,39см2; Jx=39,5см4; ix=2,31см; iy=3,42см; z0=2,02. Площадь двух уголков: Определяем λx, λy:
Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 31,32 из ∟75×5.
Раскос 31: Расчётное усилие: N=32,9893кН.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟50×4. Характеристики: А∟=3,89см2; Jx=9,21см4; ix=1,54см; iy=2,43см; z0=1,38см. Площадь двух уголков: Определяем λx, λy:
Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 31 из ∟50×4. Стойки 19,25 Расчётное усилие: N=-50,8кН. Задаёмся гибкостью λ=80; Коэффициент продольного изгиба при λ=80 для стали с Ry=24кН/см2 φ=0.686
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟63×4. Характеристики: А∟=4,96см2; Jx=18,9см4; ix=1,95см; iy=2,93см; z0=1,69см. Площадь двух уголков: Определяем λx, λy:
φmin при гибкости λx=112,82: φmin=0,461 Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 19,25 из ∟63×4 Стойки 20,24: Расчётное усилие: N=-101,6кН. Задаёмся гибкостью λ=80; Коэффициент продольного изгиба при λ=80 для стали с Ry=24кН/см2 φ=0.686
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟70×4,5. Характеристики: А∟=6,2см2; Jx=29см4; ix=2,16см; iy=3,22см; z0=1,88см. Площадь двух уголков: Определяем λx, λy:
φmin при гибкости λx=115,74: φmin=0,444 Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 17,24 из ∟70×4,5 Стойки 21,23: Расчётное усилие: N=-101,6кН. Задаёмся гибкостью λ=80; Коэффициент продольного изгиба при λ=80 для стали с Ry=24кН/см2 φ=0.686
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟80×5,5 Характеристики: А∟=8,63см2; Jx=52,7см4; ix=2,47см; iy=3,64см; z0=2,17см. Площадь двух уголков: Определяем λx, λy:
φmin при гибкости λx=113,36: φmin=0,458 Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 21,23 из ∟80×5,5 Стойка 22: Расчётное усилие: N=75,3805кН.
Сечение проектируем из двух равнополочных уголков. Площадь одного уголка По сортаменту принимаем ближайший прокат: ∟50×4. Характеристики: А∟=3,89см2; Jx=9,21см4; ix=1,54см; iy=2,43см; z0=1,38см. Площадь двух уголков: Определяем λx, λy:
Несущая способность сечения:
Устойчивость (напряжение в сечении):
Определяем недонапряжение в стержнях: Окончательно принимаем сечение элемента 22 из ∟50×4.
В целях экономии металла неработающие стержни верхнего пояса 7 и 18 назначаем из 2∟ 75×8 – минимальный профиль по расчету. Все результаты расчёта сведены в таблицу 3. Таблица 3. Таблица подбора сечений элементов фермы.
Расчёт связей.
Горизонтальные связи шатра проектируем полураскосного вида из одиночных уголков. Предельная гибкость сжатых стержней связи равна 200. Сечение подбираем по заданной предельной гибкости. Определяем требуемый радиус инерции:
где
По сортаменту подбираем уголок 70´8, для которого Вертикальные связи шатра в сечении по коньку кровли проектируем крестового вида из сдвоенных уголков, работающих на растяжение. Предельная гибкость растянутых стержней связи равна 400. Сечение подбираем по заданной предельной гибкости. Определяем требуемый радиус инерции:
где
По сортаменту подбираем сечение из сдвоенных уголков 56´5, для которого Сечение распорок для нижних поясов ферм проектируем из сдвоенных уголков. Предельная гибкость сжатых стержней равна 200. Сечение подбираем по заданной предельной гибкости. Определяем требуемый радиус инерции:
где
По сортаменту подбираем сечение из сдвоенных уголков 100´10, для которого Вертикальные связи по колоннам проектируем крестового вида из одиночных уголков, работающих на растяжение. Предельная гибкость растянутых стержней связи равна 400. Сечение подбираем по заданной предельной гибкости. Определяем требуемый радиус инерции:
где
По сортаменту подбираем сечение из уголка 90´6, для которого Расчет сварных швов Сварка узлов фермы выполняется полуавтоматом сварочной проволокой СВ-10ГА. Расчётные сопротивления угловых швов: — по металлу шва: — по металлу границы сплавления: Вf = 0,9–коэффициент глубины проплавления по металлу шва; Вz = 1,05–коэффициент глубины проплавления по металлу границы сплавления; Rwf – расчётное сопротивление металла шва – по таблице 56 СНиП II-23-81 (1990) «Стальные конструкции»; Rwz – расчётное сопротивление границы сплавления Run – нормативное значение временного сопротивления (предел прочности при растяжении). Так как
Рассмотрим опорный узел А: Рассчитываем прикрепление опорного раскоса 26, расчётное усилие
Для крепления нижнего пояса 1 расчётное усилие 2∟ 75×8.
Для крепления стойки 19 расчётное усилие
Рассмотрим узел В: Рассчитываем прикрепление раскоса 27, расчётное усилие
Раскос 26:
Для крепления верхнего пояса 8 расчётное усилие 2∟ 125×10.
Рассмотрим узел С: Рассчитываем прикрепление раскоса 28, расчётное усилие
Раскос 27:
Крепление к фасонке стойки 20 рассчитываем при
Нижний пояс 1:
Для крепления нижнего пояса 2 расчётное усилие 2∟ 125×10.
Рассмотрим узел D: Узловая нагрузка Стойка 20:
Для крепления верхнего пояса8,9 расчётное усилие 2∟ 125×10.
Рассмотрим узел Е: Рассчитываем прикрепление раскоса 29, расчётное усилие
Раскос 28:
Для крепления верхнего пояса 9,10 расчётное усилие (средние)
Рассмотрим узел F: Рассчитываем прикрепление раскоса 30, расчётное усилие
Раскос 29:
Крепление к фасонке стойки 21 рассчитываем при
Для крепленияножнего пояса 2,3 расчётное усилие (средние)
Рассмотрим узел G:
Стойка 21:
Для крепления верхнего пояса 9,10 расчётное усилие
Рассмотрим узел H: Рассчитываем прикрепление раскоса 31, расчётное усилие
Раскос 30: Для крепления верхнего пояса 11,12 расчётное усилие (средние)
Рассмотрим узел I: Раскос 31:
Крепление к фасонке стойки 22 рассчитываем при
Для крепления нижнего пояса 3 расчётное усилие
Рассмотрим узел J: Стойка 22: Для крепления верхнего пояса 12 расчётное усилие
Толщину узловых фасонок принимаем tф=14мм – материал С255. Усилия в сварных швах распределяем: 0.7N – по обушку, 0.3N – по перу. Результаты расчётов заносим в таблицу №4. Таблица расчёта сварных швов (при γс=1.0). Таблица 4.
Катет с
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 708; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.195.79 (0.008 с.) |

 .
.


 ;
; 



 .
.

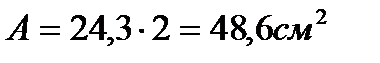
 ;
; 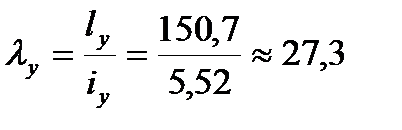



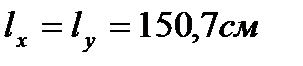 .
.


 ;
; 



 ;
; 



 ;
; 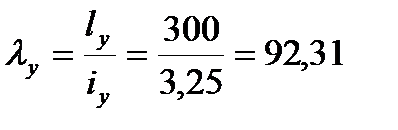



 ;
; 



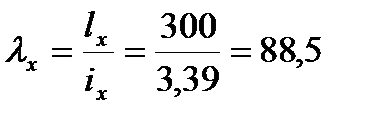 ;
; 



 ;
; 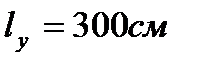



 ;
; 



 ;
; 
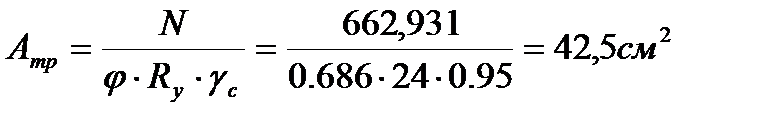


 ;
; 



 ;
; 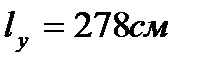


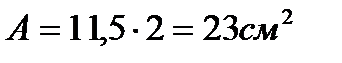
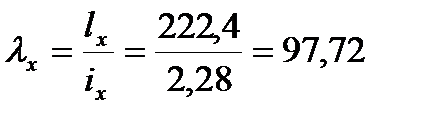 ;
; 

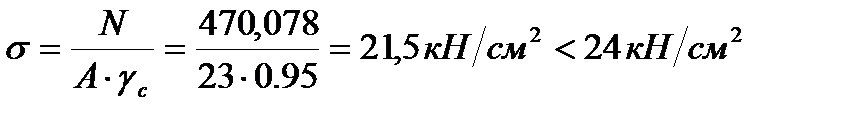

 ;
; 


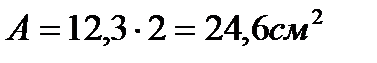
 ;
; 
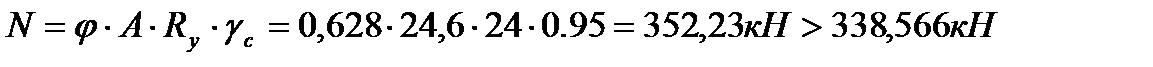


 ;
; 



 ;
; 
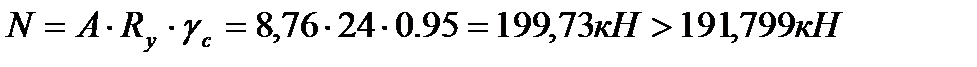


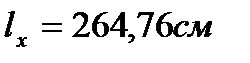 ;
; 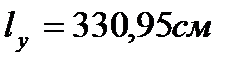



 ;
; 
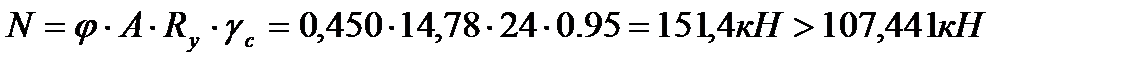


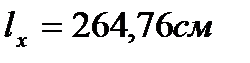 ;
; 
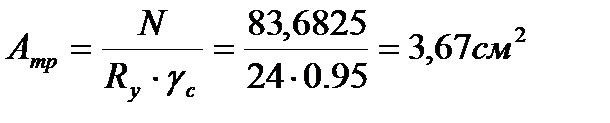

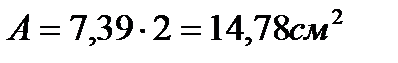
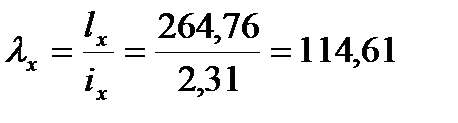 ;
; 



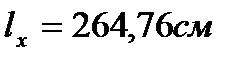 ;
; 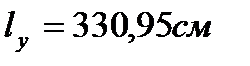



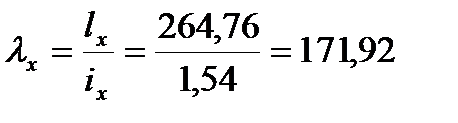 ;
; 



 ;
; 

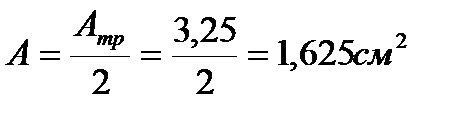

 ;
; 



 ;
; 


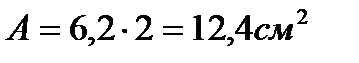
 ;
; 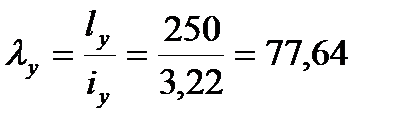



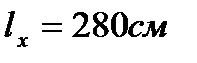 ;
; 
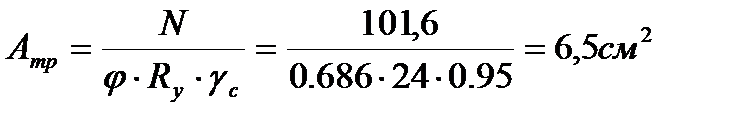
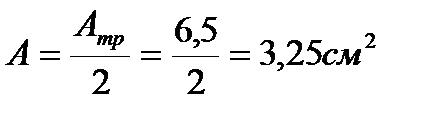

 ;
; 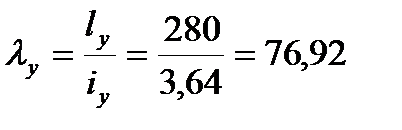



 ;
; 
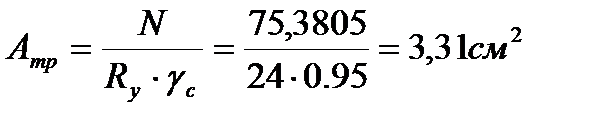

 ;
; 








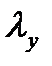
 ,
, - расчётная длина растянутого стержня в плоскости расположения связей.
- расчётная длина растянутого стержня в плоскости расположения связей. - геометрическая длина стержня.
- геометрическая длина стержня.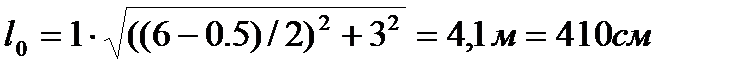 .
.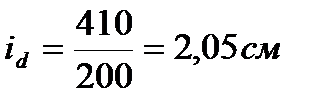 .
. .
. .
. .
.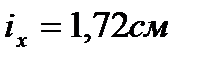 ;
; 
 .
. .
. ;
; 
 .
. .
. ;
;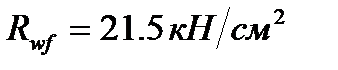 .
.
 ,
,  где
где >
> 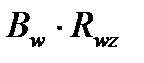 , т.е.
, т.е.  , расчёт выполняем по металлу границы сплавления.
, расчёт выполняем по металлу границы сплавления. Расчётную длину сварных швов определяем по формуле: -
Расчётную длину сварных швов определяем по формуле: -  длина сварного шва с каждой стороны фасонки.
длина сварного шва с каждой стороны фасонки.
 , сечение из 2∟ 125×10, сварка ручная.
, сечение из 2∟ 125×10, сварка ручная.

 , сечение из
, сечение из

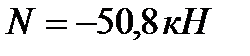 , сечение из 2∟ 63×4.
, сечение из 2∟ 63×4.

 , сечение из 2∟ 75×8, сварка ручная.
, сечение из 2∟ 75×8, сварка ручная.

 ,
,  из расчёта узла А.
из расчёта узла А.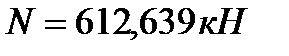 , сечение из
, сечение из

 , сечение из 2∟ 90×7, сварка ручная.
, сечение из 2∟ 90×7, сварка ручная.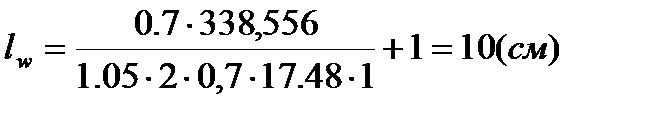
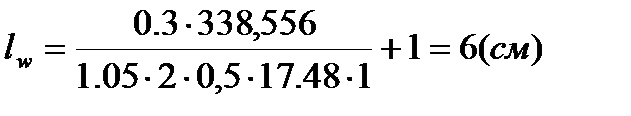
 ,
, 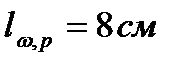 из расчёта узла В.
из расчёта узла В. , сечение из 2∟ 75×8, сварка ручная.
, сечение из 2∟ 75×8, сварка ручная.

 ,
,  из расчёта узла А
из расчёта узла А , сечение из
, сечение из
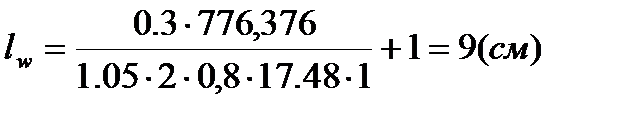
 .
. ,
,  из расчёта узла С.
из расчёта узла С. , сечение из
, сечение из
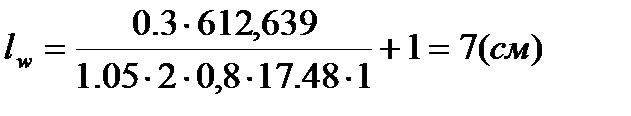
 , сечение из 2∟ 75×8, сварка ручная.
, сечение из 2∟ 75×8, сварка ручная.

 ,
, 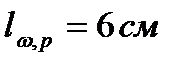 из расчёта узла С.
из расчёта узла С.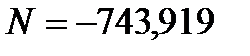 , сечение из 2∟ 125×10.
, сечение из 2∟ 125×10.

 , сечение из 2∟ 75×8, сварка ручная.
, сечение из 2∟ 75×8, сварка ручная.

 ,
,  из расчёта узла Е.
из расчёта узла Е. , сечение из 2∟ 90×7, сварка ручная.
, сечение из 2∟ 90×7, сварка ручная.
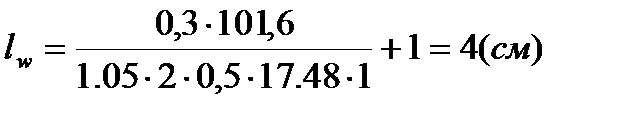
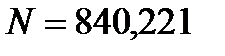 , сечение из 2∟ 125×10
, сечение из 2∟ 125×10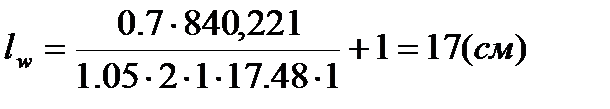

 ,
,  из расчёта узла F.
из расчёта узла F. , сечение из 2∟ 125×10.
, сечение из 2∟ 125×10.

 , сечение из 2∟ 75×8, сварка ручная.
, сечение из 2∟ 75×8, сварка ручная.

 ,
, 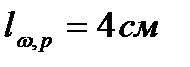 из расчёта узла F.
из расчёта узла F.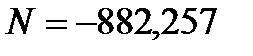 , сечение из 2∟ 125×10.
, сечение из 2∟ 125×10.

 ,
,  из расчёта узла H.
из расчёта узла H. , сечение из 2∟ 75×8, сварка ручная.
, сечение из 2∟ 75×8, сварка ручная.

 , сечение из 2∟ 125×10
, сечение из 2∟ 125×10

 ,
,  из расчёта узла I.
из расчёта узла I. , сечение из 2∟ 125×10
, сечение из 2∟ 125×10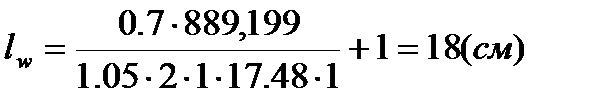
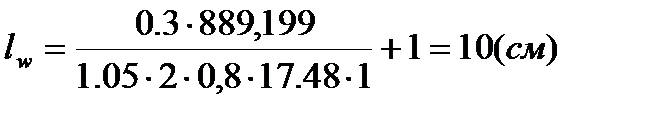
 .
.
 .
.



