
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перелік питань, що охоплюють зміст робочої програми дисципліни OMMСодержание книги
Поиск на нашем сайте
Перелік питань, що охоплюють зміст робочої програми дисципліни OMM
1. Принципи моделювання соціально-економічних систем і процесів. 2. Системний підхід у моделюванні економічних процесів та явищ. 3. Сутність економіко-математичної моделі. 4. Необхідність використання математичного моделювання економічних процесів. 5. Схема математичного моделювання економічних процесів. 6. Етапи математичного моделювання. 7. Випадковість і невизначеність процесів економічних систем. 8. Причини виникнення невизначеності в соціально-економічних системах. 9. Системні характеристики соціально-економічних систем. 10. Стійкість розвитку соціально-економічних систем. 11. Ефективність, маневреність, надійність, еластичність соціально-економічних систем. 12. Сутність адекватності економіко-математичних моделей. 13. Проблеми оцінювання адекватності моделі. Способи перевірки адекватності економіко-математичних моделей. 14. Поняття адаптації та адаптивних систем. 15. Елементи класифікації економіко-математичних моделей. 16. Сутність аналітичного та комп’ютерного моделювання. 17. Системи економіко-математичних моделей. 18. Інтегрована система економіко-математичних моделей. 19. Методологічні принципи побудови системи економіко-математичних моделей. 20. Сутність оптимізаційних моделей. Приклади економічних задач математичного програмування. 21. Загальна постановка задачі лінійного програмування. Приклади економічних задач лінійного програмування. 22. Модель задачі лінійного програмування в розгорнутому і скороченому вигляді, а також в матричній і векторній формах. 23. Властивості розв’язків задачі лінійного програмування. Геометрична інтерпретація задач лінійного програмування. 24. Означення планів задачі лінійного програмування (допустимий, опорний, оптимальний). 25. Побудова опорного плану задачі лінійного програмування, перехід до іншого опорного плану. 26. Алгоритм симплексного методу знаходження розв’язку задачі лінійного програмування. 27. Ознака оптимальності плану за симплекс-методом. Порушення ознаки оптимальності. 28. Симплексний метод із штучним базисом. 29. Двоїста задача. Правила побудови двоїстої задачі. 30. Симетричні й несиметричні двоїсті задачі. 31. Економічний зміст двоїстої задачі й двоїстих оцінок. 32. Теореми двоїстості, їх економічна інтерпретація. 33. Застосування теорем двоїстості в розв’язуванні задач лінійного програмування. 34. Аналіз розв’язків лінійних економіко-математичних моделей. Оцінка рентабельності продукції. 35. Аналіз обмежень дефіцитних і недефіцитних ресурсів. 36. Цілочислове програмування. Область застосування цілочислових задач в плануванні й управлінні виробництвом. 37. Геометрична інтерпретація задачі цілочислового програмування. 38. Метод Гоморі. 39. Економічна постановка та формалізація задач з дробово-лінійною цільовою функцією. 40. Геометрична інтерпретація задач дробово-лінійного програмування. 41. Розв’язування дробово-лінійної оптимізаційної задачі зведенням до задачі лінійного програмування. 42. Постановка задачі нелінійного програмування, математична модель. Геометрична інтерпретація. 43. Графічний метод розв’язування задач нелінійного програмування. 44. Метод множників Лагранжа. Теорема Лагранжа. Алгоритм розв’язування задачі на безумовний екстремум. 45. Поняття про опуклі функції. Геометрична інтерпретація задачі опуклого програмування на площині. 46. Сідлова точка та необхідні і достатні умови її існування. Теорема Куна - Таккера. 47. Постановка задачі квадратичного програмування та її математична модель. 48. Градієнтні методи розв’язання задач нелінійного програмування та їх класифікація. 49. Економічна сутність задач динамічного програмування. 50. Метод рекурентних співвідношень. 51. Принцип оптимальності. 52. Багатокроковий процес прийняття рішень.Принцип Беллмана. 53. Стохастичне програмування: постановка і математична модель задачі. Задачі M,V – типу. 54. Приклади економічних задач стохастичного і динамічного програмування. 55. Ризик, невизначеність та конфліктність розвитку соціально-економічних процесів. Ризикотвірні чинники. 56. Поняття ризику в економіці. Особливості прояву економічного ризику в Україні 57. Джерела, об’єкт, суб’єкт ризику. 58. Функції ризику. 59. Сприйняття ризику. Психологічні аспекти ризику. 60. Правові аспекти ризику. 61. Класифікація ризику. Ризики в маркетингу. 62. Граничні межі ризику. 63. Системний аналіз ризику в економіці. 64. Якісний аналіз ризику: керовані, некеровані, об’єктивні, суб’єктивні, зовнішні, внутрішні фактори ризику. 65. Кількісний аналіз ризику. Загальні підходи до кількісної оцінки ризику. 66. Кількісний аналіз ризику: · Ймовірність як один із підходів до оцінювання ступеня ризику. · Кількісні показники ступеня ризику в абсолютному вираженні. · Кількісні показники ступеня ризику у відносному вираженні. 67. Системний підхід в управлінні ризиком. Організаційно-методичні засади управління ризиком. 68. Методи зниження ступеня ризику. розподіл ризику: диверсифікація, лімітування, страхування. 69. Основні поняття теорії ігор 70. Класифікація ігор. 71. Матричні ігри двох осіб. Геометрична інтерпретація гри 2´2. 72. Гра зі змішаними стратегіями. 73. Зведення матричної гри до задачі лінійного програмування. 74. Гра з “ природою ”.Застосування гри з “ природою ” в економіці.
ШКАЛА ОЦІНЮВАННЯ
3. Структура екзаменаційних задач: І. Задачі лінійного програмування:
ІІ. Задачі нелінійного програмування:
4. графічний метод розв’язування задач дробово-лінійного програмування. 5. задачі стохастичного програмування. 6. задачі динамічного програмування.
IІІ. Ризикологія:
або Ігрові моделі 1. геометрична інтерпретація гри 2´2. 2. гра із “ природою ”.
Приклади типових завдань 1. Розв’язати задачі лінійного програмування графічним методом: а) Z = x1 - 2x2 (min) б) Z = x1 + 3x2 (max) x1 - x2 £ 1, x1 - x2 £ 1, x1 + x2 ³ 2, 2x1 + x2 £ 2, x1 - 2x2 £ 0, x1 - x2 ³ 0, x1³ 0; x2 ³ 0. x1³ 0; x2 ³ 0. 2. На виготовлення двох видів продукції (П1 і П2) витрачаються три види ресурсів
3. Знайти розв’язок наступних задач лінійного програмування шляхом графічного розв’язування двоїстої задачі й застосування теорем двоїстості:
 . .
4. Для плану
а)
б)
5. У наведеній задачі: а) побудуйте економіко-математичні модель початкової й двоїстої задач; б) приведіть задачі до канонічного виду й дайте економічне тлумачення основних й допоміжних змінних двох задач; в) з наведеної останньої симплекс-таблиці початкової задачі запишіть оптимальні плани г) визначте дефіцитні й недефіцитні ресурси, рентабельну та збиткову продукцію; д) знайдіть межі зміни обсягів дефіцитних ресурсів, в котрих оцінка ресурсу залишається сталою (аналіз двоїстих оцінок на стійкість).
Підприємство виготовляє три види продукції А, В і С, використовуючи для цього три види ресурсів I, II, III. Норми витрат усіх ресурсів на одиницю продукції та запаси ресурсів наведено в табл.1 Таблиця 1
Відома ціна одиниці продукції кожного виду: А - 9 ум. од., В -10 ум. од. і С - 16 ум. од. Визначити план виробництва продукції, що забезпечує підприємству найбільший доход. Остання симплекс-таблиця даної задачімає такий вигляд (табл.2) Таблиця 2
6. Розв’язати наступну задачу: компанія контролює три фабрики А1, А2, А3, здатні виготовляти 150, 60 та 80 тис. од. продукції щотижня. Компанія уклала договір з чотирма замовниками В1, В2, В3, В4, яким потрібно щотижня відповідно 110, 40, 60 та 80 тис. од. продукції. Вартість виробництва та транспортування 1000 од. продукції замовниками з кожної фабрики наведено в таблиці:
Визначити для кожної фабрики оптимальний план перевезення продукції до замовників, що мінімізує загальну вартість виробництва і транспортних послуг.
7. Записати модель транспортної задачі як задачі ЛП. Розв’язати задачу з додатковими умовами: · повністю задовольняється попит 2-ого споживача; · неможливо виконати перевезення за маршрутом А1 В3 і А3 В1.
. 8. Розв’язати дво етапну транспортну задач: побудувати перший опорний план перевезень ТЗ, перевірити його на оптимальність, побудувати цикл перерозподілу ресурсів перевезень, порівняти вартості перевезень.
9. Розв’язати графічним методом задачу нелінійного програмування; знайти глобальний екстремум:
11. Розв’язати графічним методом наступну задачу дробово-лінійного програмування:
12. За даною платіжною матрицею знайти маршрут проїзду по всіх містах, щоб вартість шляху була мінімальною.
1 ∞ 4 12 15 10 2 6 ∞ 8 12 15 3 3 4 ∞ 6 11 4 2 8 5 ∞ 6 5 7 3 6 10 ∞
13. Розв`язати гру графічно і аналітично: визначити ціну гри, частоту застосування стратегій кожного гравця.
1.
2.
3.
14. Звівши задачу « гри з природою»: фірма – зовнішнє середовище до ЗЛП, розв`язати гру - визначити ціну гри, частоту застосування кращих стратегій. 1. Власник автозаправочної станції прийняв рішення про надання додаткових послуг своїм клієнтам. Певну суму своїх грошових коштів він може витратити на організацію:
Рішення власника залежить від попиту на ті чи інші товари, який можхарактеризуватись станом: · попит на засоби догляду за автомобілем переважає попит на запчастини і попит на газети і журнали (Q1); · з трьох названих груп товарів переважає попит на запчастини (Q2); · найбільшим виявиться попит на газетно – журнальну продукцію (Q3).
Виходячи зі свого досвіду, власник склав таблицю можливих прибутків (в залежності від можливих рівнів попиту).
2. Фірма займається виробництвом прасок “SIGMA”. Її менеджери розробили 5 варіантів цін на ці праски. Обсяг реалізації товару залежить від ціни та еластичності попиту. Якою буде еластичність попиту – невідомо, бо новий вид прасок якісно відрізняється від наявних на ринку. Фірма поставила перед собою задачу завоювання ринку. Яку ціну має вибрати фірма? Відповідні дані наведені в таблиці:
ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ З РОЗДІЛУ «РИЗИКОЛОГІЯ» “ а ” – номер студента за списком:
· Дві конкуруючі корпорації намагаються контролювати всі дрібні компанії своєї галузі. Невелика фірма може ввійти до складу однієї з них, що може принести їй як прибутки, так і збитки. З метою протистояння діям корпорацій фірма може ініціювати створення асоціації дрібних підприємств. Який з варіантів обрати фірмі з позиції максимальної ефективності і мінімального рівня ризику?
· Банк змушений продати акції однієї з чотирьох компаній, які є в його портфелі цінних паперів. Рішення щодо того, які акції продавати, залежить від стану фондового ринку (економічного середовища), який може подаватися трьома варіантами Q1, Q2, Q3. Функціонал оцінювання (збитки у млн. грн., які понесе банк від реалізації акцій, бо їх курс є нижчим від того, за яким їх придбали) заданий в таблиці:
Відомо також, що стан економічного середовища Q1 може реалізуватися з ймовірністю 0,…, Q2 – з ймовірністю 0,4, Q3 – з ймовірністю 0,…. З трьох можливих варіантів виберіть таке рішення, яке було б оптимальним для банку (з позиції мінімальних сподіваних збитків) і мінімізувало би рівень ризику. ТЕМИ РЕФЕРАТІВ · Економіка як об’єкт моделювання. · Особливості та принципи математичного моделювання економічних систем і процесів. · Системний підхід у моделюванні економічних процесів та явищ. · Емерджентність соціально-економічних систем. · Випадковість і невизначеність процесів економічних систем. · Причини виникнення невизначеності в соціально-економічних системах. · Сутність адекватності економіко-математичних моделей. · Проблеми оцінювання адекватності моделі. Способи перевірки адекватності економіко-математичних моделей. · Системні характеристики соціально-економічних систем: - Стійкість розвитку соціально-економічних систем. - Ефективність соціально-економічних систем.. - Маневреність соціально-економічних систем.. - Надійність соціально-економічних систем.. - Еластичність соціально-економічних систем. · Економічна сутність задач динамічного програмування. Багатокроковий процес прийняття рішень в задачах динамічного програмування. · Стохастичне програмування. Приклади економічних задач стохастичного програмування. · Градієнтні методи розв’язання задач нелінійного програмування та їх класифікація. · Особливості прояву економічного ризику в Україні. · Системний аналіз ризику в економіці. · Правові аспекти ризику. o Сприйняття ризику. Психологічні аспекти ризику. · Особливості проведення маркетингової політики і прийняття стратегічних рішень. · Маркетинговий підхід до управління ризиком. · Диверсифікація в маркетингу. · Ризик – менеджмент в маркетингу. · Ризики в маркетингу. Класифікація ризику · Граничні межі ризику. · Управління ризиком в умовах невизначеності. · Системний підхід в управлінні ризиком. · Методи зниження ступеня ризику. розподіл ризику: диверсифікація, лімітування, страхування. АБО Провести якісний аналіз ризиків або порівняльний аналіз ризикованості в діяльності підприємств, які займаються: - виробництвом молочної продукції; - виробництвом хлібо-булочної продукції; - виробництвом м’ясної продукції; - виробництвом кондитерської продукції; - виробництвом пива; - виробництвом меблів; - зборкою і ремонтом автомобілів; - продажем мобільних телефонів; - торгівельною діяльністю; - видавничою діяльністю тощо.
В аналізі виділити, використовуючи схему маркетингових ризиків, зовнішні і внутрішні, керовані і некеровані, суб’єктивні й об’єктивні фактори ризику. Вказати можливі способи управління цими ризиками, шляхи подолання негативних наслідків.
ЕКОНОМЕТРИКА Зміст дисципліни за темами Тема 5. Мультиколінеарність
Моделі з порушенням передумов використання МНК: мультиколінеарність. Мультиколінеарність: її суть та наслідки. Тестування наявності мультиколінеарності в моделі. Алгоритм Фаррара-Глобера. Методи усунення мультиколінеарності.
ШКАЛА ОЦІНЮВАННЯ
Приклади типових завдань. 1. Розрахувати економетричну модель парної регресії між факторами Х і У: Ŷ = ǎ0 + ǎ1·х. Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1. · Розрахувати за нею прогнозоване значення залежного фактора Упр · Побудувати графік моделі парної регресії в кореляційному полі – “хмарі розсіювання”. · Розрахувати коефіцієнт детермінації R2 і коефіцієнт кореляції R. . Який зміст цих коефіцієнтів? · Оцінити якість отриманої моделі за F-, t – критеріями з рівнем значущості α = 0,05. .
Х – витрати на маркетинг, (тис. грн..), У – прибуток, (млн. грн.).
2. В результаті дослідження чинників економічного зростання побудовано таку модель (обсяг вибірки – 73 країни): Y = 1,4 – 0,52X (5,9) (4,34) (3,91) (0,79) (2,7) де Y – темп росту середнього значення ВВП на душу населення у % до базового періоду; X X X X4 – зовнішній борг, % до ВВП; X В дужках вказані спостережувані значення t-критерія. Відомий також коефіцієнт детермінації R2 = 0,78. 1) Перевірити загальну якість даної моделі. 2) Перевірити значущість параметрів моделі при рівні значущості a = 0,05 та записати, враховуючи зроблені висновки, теоретичну модель. 3) Побудувати довірчі інтервали для параметрів теоретичної моделі при рівні надійності g = 0,95. 4) Визначити частинні коефіцієнти еластичності. 5) Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1. 3. Побудовано модель залежності середньомісячної ринкової ціни акцій підприємства (Y, грн./акція) від обсягу сплачених дивідендів на акцію (Х1, грн./місяць) та обсягу коштів, спрямованих підприємством на розширення виробництва (Х2, сотні тис. грн. /місяць): yi = 2,4 + 1,6 хi1 + 0,9 хi2 + еi. Відомо також, що 1) Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1. 2) Побудувати точковий та інтервальні прогнози для залежної змінної, якщо хпр.1 = 10, хпр.2 = 2, а рівень надійності g = 0,95.
4. Розрахована регресійна модель залежності прибутку (У) від інвестицій (Х1), основного фонду виробництва (Х2 ), фонду робочого часу (Х3) за 20 спостереженнями:
. 1. Перевірити загальну якість даної моделі. 2. Перевірити значущість параметрів моделі при рівні значущості a = 0,05 та записати, враховуючи зроблені висновки, теоретичну модель. 3. Побудувати довірчі інтервали для параметрів теоретичної моделі. 4. Визначити частинні коефіцієнти еластичності. 5. Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1. 5. Аналізується прибуток підприємства Y (млн.$) в залежності від витрат на рекламу Х (млн.$). За спостереженнями на протязі 9 років отримані наступні дані:
1) Побудуйте кореляційне поле і висуньте гіпотезу, щодо виду залежності між показниками. 2) Оцініть за МНК параметри лінійної регресії Y = 3) Оцініть якість побудованої регресії. 4) Знайдіть за допомогою МНК оцінки параметрів квадратичної регресії Y = 5) Оцініть якість побудованої моделі. Яку з моделей варто обрати для подальшого дослідження?
6. Для двох видів продукції А і В моделі залежності питомих постійних витрат від об’єму випущеної продукції мають вигляд: YА = 80 + 0,7х, YВ= 40 1) Визначити коефіцієнти еластичності по кожному виду продукції та пояснити їх зміст. 2) Порівняти еластичність затрат для обох видів продукції при х =1000. 3) Визначити, яким повинен бути об’єм випущеної продукції, щоб коефіцієнти еластичності для продукції А та В стали рівними.
7. Нехай Y = Середнє значення змінної Y для 15 чоловіків дорівнює 5, для 25 жінок – 3. При цьому відомо, що дисперсія залишків становить 64.
Визначте оцінку коефіцієнтів
8. При аналізі залежності заробітної плати (S) 70 співробітників фірми (45 чоловіків і 25 жінок) від стажу роботи (Т) на фірмі отримані наступні регресійні моделі: S = 50+ 0,12 Т, R2 = 0,63, t = (5,23) (9,35). S = 30 + 0,092 T + 25D, R2 = 0,72, t = (4,63) (4,3) (6,23). S = 25 + 0,078 T+32D + 0,07T ·D, R2 = 0,912, t = (3,07) (3,73) (2,93) (1,98) де D - фіктивна змінна, що відображає стать співробітника.
а) Яка з регресій (1 або 2), (2 або 3) з вашого погляду є більш раціональною? б) Які похибки при виборі регресії 1 допускаються? в) Поясніть зміст кожного з коефіцієнтів у рівнянні регресії. г) Якою буде середня зарплата співробітника – чоловіка і жінки зi стажем роботи у 15 років?
9. В нижченаведеній таблиці Y – місячний обсяг попиту на товари першої необхідності сім’ї з трьох чоловік (ум.гр.од.), Х – місячний рівень доходу сім’ї (ум.гр.од.):
Перевірити, яка з моделей краще наближає емпіричні дані: лінійна, степенева чи гіперболічна. Перевірити статистичну значущість зв’язку в кожній з цих моделей.
10. Відомі дані щодо середньомісячного рівня зайнятості (Х, %) та рівня інфляції (Y, %):
Побудувати гіперболічну модель, визначити коефіцієнт детермінації та коефіцієнт еластичності.
11.. За даними 15 років побудовані два рівняння регресії: 1) Y = 3,435 - 0,5145Х+ ε, R2 = 0,6748; t = (20,5) (4.3) 2) 1n Y = 0,851 - 0,2514Х+ ε, R2 = 0,7785, t = (43,6) (5,2) де Y - щоденне середньодушове споживання кави (у чашках 100г), X - середньорічна ціна кави (грн/кг). а) Проаналізуйте коефіцієнти кожної з моделей. б) Чи можна за визначеними моделями визначити, чи є попит на каву еластичним? в) Яка модель, з вашого погляду, є переважнішою? Чи можна обґрунтувати висновок за коефіцієнтами детермінації? 12. Для 3-х пояснюючих змінних обчислено кореляційну матрицю r. Чи існує в масиві змінних мультиколінеарність? За оберненою до неї матрицею оцінити попарну мультиколінеарність змінних для 15 спостережень і 95% надійності:
13. Відомі дані щодо місячного обсягу прибутку 15 підприємств галузі – Х (млн.грн), та обсягу дивідендів, сплачених цими підприємствами за місяць – Y (млн.грн):
Побудувати модель парної лінійної регресії. Перевірити за тестом Гельдфельда-Квандта, чи виконується умова гомоскедастичності залишків.
14. Обчислити коефіцієнт автокореляції залишків першого порядку:
Зробити висновки щодо наявності автокореляції за критерієм Дарбіна-Уотсона.
Зразок екзаменаційного білету
1. Використання економетричних моделей для прийняття управлінських рішень та прогнозування. 2. Врахування якісних факторів в лінійних економетричних моделях за допомогою фіктивних змінних. 3. Поняття системи одночасних економетричних рівнянь.
4. Розрахувати економетричну модель парної регресії між факторами Х і Y: Ŷ = ǎ0 + ǎ1·х+ ε. · Побудувати графік моделі парної регресії в кореляційному полі. · Розрахувати за нею прогнозоване значення залежного фактора Yпр · Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1
Х – енергомісткість праці на 1 робітника (кВт/ роб), Y – продуктивність праці (тис. грн./роб.).
5. Для 30 підприємств галузі була досліджена залежність річного обсягу випуску продукції Y (млн. грн.) від чисельності працюючих на виробництві Х1 (чоловік) та середньорічної вартості основних фондів Х2 (млн. грн.):
6. Обчислити коефіцієнт автокореляції залишків першого порядку:
Зробити висновки щодо наявності автокореляції за критерієм Дарбіна-Уотсона для регресійної моделі із 2-ма змінними.
Перелік питань, що охоплюють зміст робочої програми дисципліни OMM
1. Принципи моделювання соціально-економічних систем і процесів. 2. Системний підхід у моделюванні економічних процесів та явищ. 3. Сутність економіко-математичної моделі. 4. Необхідність використання математичного моделювання економічних процесів. 5. Схема математичного моделювання економічних процесів. 6. Етапи математичного моделювання. 7. Випадковість і невизначеність процесів економічних систем. 8. Причини виникнення невизначеності в соціально-економічних системах. 9. Системні характеристики соціально-економічних систем. 10. Стійкість розвитку соціально-економічних систем. 11. Ефективність, маневреність, надійність, еластичність соціально-економічних систем. 12. Сутність адекватності економіко-мате
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.220 (0.012 с.) |


 Наявність ресурсів дорівнює відповідно: 361, 520, 248. Витрати ресурсів на одиницю продукції П1 становлять відповідно: 13, 7, 17; на одиницю продукції П2 - 16, 4, 9. Ціна за одиницю продукції дорівнює відповідно: 11, 8. Побудувати модель початкової й двоїстої задач. Знайти такий план виробництва, який би забезпечував найбільшу виручку. Дати економічне тлумачення розв’язків задач.
Наявність ресурсів дорівнює відповідно: 361, 520, 248. Витрати ресурсів на одиницю продукції П1 становлять відповідно: 13, 7, 17; на одиницю продукції П2 - 16, 4, 9. Ціна за одиницю продукції дорівнює відповідно: 11, 8. Побудувати модель початкової й двоїстої задач. Знайти такий план виробництва, який би забезпечував найбільшу виручку. Дати економічне тлумачення розв’язків задач.

 визначити, чи він є оптимальним для наступних задач (застосовуючи теореми двоїстості, не розв’язуючи задачі симплексним методом):
визначити, чи він є оптимальним для наступних задач (застосовуючи теореми двоїстості, не розв’язуючи задачі симплексним методом):



 і
і 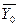 ;
;




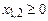 .
. 10. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму задачі нелінійного програмування:
10. Використовуючи метод множників Лагранжа, знайти точки умовного екстремуму задачі нелінійного програмування: 

 за умов
за умов 
 1 2 3 4 5
1 2 3 4 5
 + 0,17 X
+ 0,17 X  + 11,16 X
+ 11,16 X  – 0,38 X
– 0,38 X  – 4,75 X
– 4,75 X  +
+  ,
, – реальні середні значення ВВП на душу населення, %;
– реальні середні значення ВВП на душу населення, %; – бюджетний дефіцит у % до ВВП;
– бюджетний дефіцит у % до ВВП; = 10,5,
= 10,5,  , n = 20.
, n = 20. /
/ .
.
 , де С – фіктивна змінна, що відображає стать суб’єкта дослідження (С=0 для жінок і С =1 для чоловіків).
, де С – фіктивна змінна, що відображає стать суб’єкта дослідження (С=0 для жінок і С =1 для чоловіків). та
та 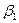 .
.



