
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Тема 9. Системи одночасних рівнянь ⇐ ПредыдущаяСтр 3 из 3
Поняття системи економетричних рівнянь. Структурна та зведена форми системи рівнянь. Ідентифікація. Необхідна і достатня умова ідентифікації. Оцінювання параметрів систем одночасних рівнянь.
ШКАЛА ОЦІНЮВАННЯ
Приклади типових завдань. 1. Розрахувати економетричну модель парної регресії між факторами Х і У: Ŷ = ǎ0 + ǎ1·х. Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1. · Розрахувати за нею прогнозоване значення залежного фактора Упр · Побудувати графік моделі парної регресії в кореляційному полі – “хмарі розсіювання”. · Розрахувати коефіцієнт детермінації R2 і коефіцієнт кореляції R. . Який зміст цих коефіцієнтів? · Оцінити якість отриманої моделі за F-, t – критеріями з рівнем значущості α = 0,05. .
Х – витрати на маркетинг, (тис. грн..), У – прибуток, (млн. грн.).
2. В результаті дослідження чинників економічного зростання побудовано таку модель (обсяг вибірки – 73 країни): Y = 1,4 – 0,52X (5,9) (4,34) (3,91) (0,79) (2,7) де Y – темп росту середнього значення ВВП на душу населення у % до базового періоду; X X X X4 – зовнішній борг, % до ВВП; X В дужках вказані спостережувані значення t-критерія. Відомий також коефіцієнт детермінації R2 = 0,78. 1) Перевірити загальну якість даної моделі. 2) Перевірити значущість параметрів моделі при рівні значущості a = 0,05 та записати, враховуючи зроблені висновки, теоретичну модель. 3) Побудувати довірчі інтервали для параметрів теоретичної моделі при рівні надійності g = 0,95. 4) Визначити частинні коефіцієнти еластичності. 5) Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1.
3. Побудовано модель залежності середньомісячної ринкової ціни акцій підприємства (Y, грн./акція) від обсягу сплачених дивідендів на акцію (Х1, грн./місяць) та обсягу коштів, спрямованих підприємством на розширення виробництва (Х2, сотні тис. грн. /місяць): yi = 2,4 + 1,6 хi1 + 0,9 хi2 + еi. Відомо також, що 1) Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1. 2) Побудувати точковий та інтервальні прогнози для залежної змінної, якщо хпр.1 = 10, хпр.2 = 2, а рівень надійності g = 0,95.
4. Розрахована регресійна модель залежності прибутку (У) від інвестицій (Х1), основного фонду виробництва (Х2 ), фонду робочого часу (Х3) за 20 спостереженнями:
. 1. Перевірити загальну якість даної моделі. 2. Перевірити значущість параметрів моделі при рівні значущості a = 0,05 та записати, враховуючи зроблені висновки, теоретичну модель. 3. Побудувати довірчі інтервали для параметрів теоретичної моделі. 4. Визначити частинні коефіцієнти еластичності. 5. Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1. 5. Аналізується прибуток підприємства Y (млн.$) в залежності від витрат на рекламу Х (млн.$). За спостереженнями на протязі 9 років отримані наступні дані:
1) Побудуйте кореляційне поле і висуньте гіпотезу, щодо виду залежності між показниками. 2) Оцініть за МНК параметри лінійної регресії Y = 3) Оцініть якість побудованої регресії. 4) Знайдіть за допомогою МНК оцінки параметрів квадратичної регресії Y = 5) Оцініть якість побудованої моделі. Яку з моделей варто обрати для подальшого дослідження?
6. Для двох видів продукції А і В моделі залежності питомих постійних витрат від об’єму випущеної продукції мають вигляд: YА = 80 + 0,7х, YВ= 40 1) Визначити коефіцієнти еластичності по кожному виду продукції та пояснити їх зміст. 2) Порівняти еластичність затрат для обох видів продукції при х =1000.
3) Визначити, яким повинен бути об’єм випущеної продукції, щоб коефіцієнти еластичності для продукції А та В стали рівними.
7. Нехай Y = Середнє значення змінної Y для 15 чоловіків дорівнює 5, для 25 жінок – 3. При цьому відомо, що дисперсія залишків становить 64.
Визначте оцінку коефіцієнтів
8. При аналізі залежності заробітної плати (S) 70 співробітників фірми (45 чоловіків і 25 жінок) від стажу роботи (Т) на фірмі отримані наступні регресійні моделі: S = 50+ 0,12 Т, R2 = 0,63, t = (5,23) (9,35). S = 30 + 0,092 T + 25D, R2 = 0,72, t = (4,63) (4,3) (6,23). S = 25 + 0,078 T+32D + 0,07T ·D, R2 = 0,912, t = (3,07) (3,73) (2,93) (1,98) де D - фіктивна змінна, що відображає стать співробітника.
а) Яка з регресій (1 або 2), (2 або 3) з вашого погляду є більш раціональною? б) Які похибки при виборі регресії 1 допускаються? в) Поясніть зміст кожного з коефіцієнтів у рівнянні регресії. г) Якою буде середня зарплата співробітника – чоловіка і жінки зi стажем роботи у 15 років?
9. В нижченаведеній таблиці Y – місячний обсяг попиту на товари першої необхідності сім’ї з трьох чоловік (ум.гр.од.), Х – місячний рівень доходу сім’ї (ум.гр.од.):
Перевірити, яка з моделей краще наближає емпіричні дані: лінійна, степенева чи гіперболічна. Перевірити статистичну значущість зв’язку в кожній з цих моделей.
10. Відомі дані щодо середньомісячного рівня зайнятості (Х, %) та рівня інфляції (Y, %):
Побудувати гіперболічну модель, визначити коефіцієнт детермінації та коефіцієнт еластичності.
11.. За даними 15 років побудовані два рівняння регресії: 1) Y = 3,435 - 0,5145Х+ ε, R2 = 0,6748; t = (20,5) (4.3) 2) 1n Y = 0,851 - 0,2514Х+ ε, R2 = 0,7785, t = (43,6) (5,2) де Y - щоденне середньодушове споживання кави (у чашках 100г), X - середньорічна ціна кави (грн/кг). а) Проаналізуйте коефіцієнти кожної з моделей. б) Чи можна за визначеними моделями визначити, чи є попит на каву еластичним? в) Яка модель, з вашого погляду, є переважнішою? Чи можна обґрунтувати висновок за коефіцієнтами детермінації? 12. Для 3-х пояснюючих змінних обчислено кореляційну матрицю r. Чи існує в масиві змінних мультиколінеарність? За оберненою до неї матрицею оцінити попарну мультиколінеарність змінних для 15 спостережень і 95% надійності:
13. Відомі дані щодо місячного обсягу прибутку 15 підприємств галузі – Х (млн.грн), та обсягу дивідендів, сплачених цими підприємствами за місяць – Y (млн.грн):
Побудувати модель парної лінійної регресії. Перевірити за тестом Гельдфельда-Квандта, чи виконується умова гомоскедастичності залишків.
14. Обчислити коефіцієнт автокореляції залишків першого порядку:
Зробити висновки щодо наявності автокореляції за критерієм Дарбіна-Уотсона.
Зразок екзаменаційного білету
1. Використання економетричних моделей для прийняття управлінських рішень та прогнозування. 2. Врахування якісних факторів в лінійних економетричних моделях за допомогою фіктивних змінних.
3. Поняття системи одночасних економетричних рівнянь.
4. Розрахувати економетричну модель парної регресії між факторами Х і Y: Ŷ = ǎ0 + ǎ1·х+ ε. · Побудувати графік моделі парної регресії в кореляційному полі. · Розрахувати за нею прогнозоване значення залежного фактора Yпр · Охарактеризувати економічний зміст оцінок параметрів моделі ǎ0, ǎ1
Х – енергомісткість праці на 1 робітника (кВт/ роб), Y – продуктивність праці (тис. грн./роб.).
5. Для 30 підприємств галузі була досліджена залежність річного обсягу випуску продукції Y (млн. грн.) від чисельності працюючих на виробництві Х1 (чоловік) та середньорічної вартості основних фондів Х2 (млн. грн.):
6. Обчислити коефіцієнт автокореляції залишків першого порядку:
Зробити висновки щодо наявності автокореляції за критерієм Дарбіна-Уотсона для регресійної моделі із 2-ма змінними.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.150.59 (0.028 с.) |
 + 0,17 X
+ 0,17 X  + 11,16 X
+ 11,16 X  – 0,38 X
– 0,38 X  – 4,75 X
– 4,75 X  +
+  ,
, – реальні середні значення ВВП на душу населення, %;
– реальні середні значення ВВП на душу населення, %; – бюджетний дефіцит у % до ВВП;
– бюджетний дефіцит у % до ВВП; = 10,5,
= 10,5,  , n = 20.
, n = 20. /
/ .
.
 , де С – фіктивна змінна, що відображає стать суб’єкта дослідження (С=0 для жінок і С =1 для чоловіків).
, де С – фіктивна змінна, що відображає стать суб’єкта дослідження (С=0 для жінок і С =1 для чоловіків). та
та 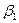 .
.



