Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кінематика рівнозмінного рухуСодержание книги Поиск на нашем сайте
21. Що характеризує тангенціальне прискорення аt матеріальної точки?
А) Бистроту зміни напрямку вектора швидкості. Г) Зміну швидкості за величиною. Б) Бистроту зміни модуля вектора швидкості. Д) Зміну напрямку вектора швидкості. В) Бистроту зміни модуля вектора переміщення.
22. Що характеризує нормальне прискорення аn матеріальної точки?
А) Бистроту зміни модуля вектора переміщення. Г) Зміну швидкості за величиною. Б) Бистроту зміни модуля вектора швидкості. Д) Зміну напрямку вектора швидкості. В) Бистроту зміни напрямку вектора швидкості.
23. Який із приведених виразів визначає повне прискорення а матеріальної точки у певний момент часу t=t1?
А)
24. Тіло рухається прямолінійно і рівноприскорено. Вкажіть умову, при якій здійснюється цей рух.
А) an=const, аt=0. Б) an=0, аt=const. В) an=const, аt=const. Г) an=0, аt=0 . Д) an=0, аt=f(t).
25. Матеріальна точка рухається прямолінійно за законом: S=2,1+0,2t2+0,1t3 м. Чому дорівнює середня швидкість Vcep за перші 3 секунди руху?
А) Vcеp=2,01 м/с. Б) Vcеp=1,84 м/с. В) Vcеp=1,24 м/с. Г) Vcеp=0,96 м/с. Д) Vcеp=1,50 м/с.
26. Матеріальна точка рухається прямолінійно за законом: S=2,1+0,2t2+0,1t3 м. Чому дорівнює середнє прискорення acep за перші 3 секунди руху?
А) acеp=1,3 м/с2. Б) acеp=0,9 м/с2. В) acеp=0,7 м/с2. Г) acеp=1,5 м/с2. Д) acеp=1,1 м/с2.
27. Матеріальна точка рухається прямолінійно згідно закону: S=1-3t+4t2-0,1t3 м. Розрахувати середню швидкість Vcep матеріальної точки за перші 3 секунди руху.
А) 9,6 м/с. Б)10,4 м/с. В)8,1 м/с. Г)12,5 м/с. Д) 7,2 м/с.
28. Матеріальна точка рухається прямолінійно згідно закону: S=1-3t+4t2-0,1t3 м. Розрахувати середнє прискорення acep матеріальної точки за перші 3 секунди руху.
А) 6,4 м/с2. Б)3,2 м/с2. В) 8,6м/с2. Г) 2,8 м/с2. Д) 7,1 м/с2.
29. Матеріальна точка рухається по колу радіусом R =5 м згідно закону S=5-2t-3t2+2t3 м. Визначте повне прискорення a цієї точки через t =2 с після початку її руху?
А) 18,5 м/с2. Б) 26,9 м/с2. В) 16,1 м/с2. Г) 20,4 м/с2. Д) 14,2 м/с2.
30. Тіло, що рухається рівносповільнено, пройшло за t =8 с шлях S =180 м, і після цього ще має швидкість V =5 м/с. Визначте початкову швидкість цього тіла V0.
А) 45 м/с. Б) 16 м/с. В) 36 м/с. Г) 40 м/с. Д) 24 м/с.
31. Тіло, рухаючись рівноприскорено, в кінці першої секунди від початку руху мало швидкість V1 =1 м/с. Яка швидкість тіла в кінці п'ятої секунди його руху V5?
А) 5 м/с. Б) 15 м/с. В) 2,5 м/с. Г) 10 м/с. Д) 7,5 м/с.
32. Потяг через t =10 с після початку руху набуває швидкості V1 =0,6 м/с. Через скільки часу від початку руху швидкість потяга дорівнюватиме V2 =3 м/с, якщо рух потягу рівноприскорений?
А) 60 с. Б) 40 с. В) 20 с. Г) 50 с. Д) 30 с.
33. Чому дорівнює швидкість тіла в кінці шостої секунди від початку руху V6, якщо, рухаючись рівноприскорено зі стану спокою, в кінці першої секунди воно досягло швидкості V1 =2 м/с? А) 24 м/с. Б) 15 м/с. В) 9 м/с. Г) 18 м/с. Д) 12 м/с.
34. Гальмуючись від початкової швидкості V0 =72 км/год зі сталим прискоренням, автомобіль зупинився за t =5 секунд. Обчислити дистанцію гальмування S.
А) 40 м. Б) 55 м. В) 50 м. Г) 45 м. Д) 35 м.
35. Тіло, рухаючись рівноприскорено без початкової швидкості, пройшло від початку руху S =60 м і набуло швидкості V =12 м/с. Визначити час руху тіла t.
А) 7,5 с. Б) 10,0 с. В) 12,5 с. Г) 20,0 с. Д) 15,0 с.
36. Тіло рухається зі стану спокою зі сталим прискоренням а =2 м/с2 і пройшло шлях S =25 м. Визначити час руху цього тіла t.
А) 13 с. Б) 7 с. В) 11 с. Г) 5 с. Д) 9 с.
37. За який проміжок часу t автомобіль, рухаючись із прискоренням а =0,4 м/с2, збільшить свою швидкість від V1 =12 м/с до V2 =20 м/с?
А) 20 c. Б) 10 с. В) 25 с. Г) 5 с. Д) 15 с.
38. Тіло рухається прямолінійно без початкової швидкості із прискоренням а =0,6 м/с2. Який шлях DS воно пройде за десяту секунду свого руху?
А) 6,4 м. Б) 3,6 м. В) 10,4 м. Г) 5,7 м. Д) 4,5 м.
39. За восьму секунду руху тіло пройшло відстань DS8 =30 м. Початкова швидкість руху дорівнює нулю. Який шлях тіло пройде за вісім секунд S8, якщо рух рівноприскорений?
А) 112 м. Б) 128 м. В) 84 м. Г) 141 м. Д) 96 м.
40. Потяг, що рухався рівномірно зі швидкістю V0 =36 км/год, почав рухатись рівноприскорено, і на шляху S =50 м його швидкість стала рівною V =15 м/с. Визначити час t рівноприскореного руху поїзда.
А) 4 с. Б) 12 с. В) 15 с. Г) 8 с. Д) 18 с.
41. Тіло, рухаючись рівноприскорено зі стану спокою, за п'яту секунду свого руху пройшло шлях DS5 =18 м. З яким прискоренням а рухалось тіло?
А) 10 м/с2. Б) 6 м/с2. В) 2 м/с2. Г) 8 м/с2. Д) 4 м/с2.
42. Тіло, рухаючись рівноприскорено зі стану спокою, за п'яту секунду свого руху пройшло шлях DS5 =18 м. Який шлях S пройшло за t =5 секунд?
А) 35 м. Б) 50 м. В) 40 м. Г) 45 м. Д) 60 м.
43. Потяг, що рухається рівносповільнено, у момент включення секундоміра мав швидкість V1 =10 м/с, а через 5 с його швидкість дорівнювала V2 =5 м/с. Визначите прискорення a, із яким рухався потяг.
А) -2,0 м/с2. Б) -0,5 м/с2. В) -1,0 м/с2. Г) -1,5 м/с2. Д) -2,5 м/с2.
44. Кулька, скочуючись із похилого жолобу зі стану спокою, за першу секунду руху пройшла шлях S1 =10 см. Який шлях пройде кулька за три секунди свого руху S3?
А) 60 см. Б) 100 см. В) 30 см. Г) 90 см. Д) 70 см.
45. За який проміжок часу автомобіль, рухаючись зі стану спокою із прискоренням а =0,6 м/с2, пройде шлях S =30 м?
А) 8 с. Б) 12 с. В) 15 с. Г) 6 с. Д) 10 с.
46. Із яким прискоренням рухається снаряд у стволі гармати, якщо довжина її ствола l =3 м, а час руху t дорівнює 0,009 с?
А) 68 км/с2. Б) 49 км/с2. В) 74 км/с2. Г) 56 км/с2. Д) 81 км/с2.
47. Яку швидкість V придбає ракета, що рухається зі стану спокою iз прискоренням a =60 м/с2 на шляху S =750 м?
А) 300 м/с. Б) 150 м/с. В) 350 м/с. Г) 250 м/с. Д) 200 м/с.
48. Куля при вильоті зі ствола автомату має швидкість V =715 м/с. Довжина ствола l =41,5 см. Із яким прискоренням a рухається куля у його стволі?
А) 484 м/с2. Б) 616 м/с2. В) 532 м/с2. Г) 648 м/с2. Д) 581 м/с2.
49. Куля при вильоті зі ствола автомату має швидкість V =715 м/с. Довжина ствола l =41,5 см. Скільки часу t рухається куля у стволі?
А) 4,64 мс. Б) 2,32 мс. В) 0,96 мс. Г) 3,48 мс. Д) 1,16 мс.
50. При швидкості руху V1 =15 км/год, гальмовий шлях автомобіля S1 дорівнює 1,5 метра. Яким буде його гальмовий шлях S2 при швидкості V2 =90 км/год при однаковому прискоренні?
А) 45 м. Б) 61 м. В) 38 м. Г) 54 м. Д) 32 м.
51. Маючи початкову швидкість V0 =36 км/год, тролейбус пройшов шлях S =120 м за t =10 с. Із яким прискоренням a рухався тролейбус?
А) 0,4 м/с2. Б) 0,8 м/с2. В) 0,2 м/с2. Г) 1,0 м/с2. Д) 0,6 м/с2.
52. Маючи початкову швидкість V0 =36 км/год, тролейбус пройшов шлях S =120 м за t =10 с. Яку швидкість V мав тролейбус наприкінці руху?
А) 10 м/с. Б) 16 м/с. В) 12 м/с. Г) 8 м/с. Д) 14 м/с.
53. Ухил довжиною L =100 м лижник подолав за t =20 с, рухаючись із прискоренням a =0,3 м/с2. Якою була швидкість лижника V0 на початку цього ухилу?
А) 3,0 м/с. Б) 1,5 м/с. В) 2,0 м/с. Г) 2,5 м/с. Д) 3,5 м/с.
54. Ухил довжиною L =100 м лижник подолав за t =20 с, рухаючись із прискоренням a =0,3 м/с2. Якою була швидкість лижника V наприкінці цього ухилу?
А) 5,5 м/с. Б) 8,0 м/с. В) 6,5 м/с. Г) 7,0 м/с. Д) 7,5 м/с.
55. Потяг пройшов під ухил за t =20 с шлях S =340 м і розвив швидкість V =19 м/с. Із яким прискоренням а рухався потяг?
А) 0,5 м/с2. Б) 0,1 м/с2. В) 0,4 м/с2. Г) 0,2 м/с2. Д) 0,6 м/с2.
56. Потяг пройшов під ухил за t =20 с шлях S =340 м і розвив швидкість V =19 м/с. Якою була його початкова швидкість V0?
А) 15 м/с. Б) 11 м/с. В) 17 м/с. Г) 9 м/с. Д) 13 м/с. 57. Якої швидкості V досягне ракета, рухаючись зі стану спокою із прискоренням a = =100 м/с2 до кінцевої висоти h =1 км?
А) 494 м/с. Б) 383 м/с. В) 447 м/с. Г) 526 м/с. Д) 412 м/с.
Ріномінний обертальний рух
58. У якому із приведених співвідношень допущена помилка? А) аt=e×R. Б) аt=v×R2. В) V=v×R. Г) v=v0±et. Д) 59. У якому із приведених співвідношень допущена помилка? А) 60. У якому із кінематичних співвідношень допущена помилка? А) 61. У якому із кінематичних співвідношень допущена помилка? А) 62. У якому iз кінематичних співвідношень допущена помилка? А) w=w0±et. Б) 63. Що характеризує тангенціальне прискорення аt?
А) Бистроту зміни вектора швидкості. Г) Бистроту зміни напрямку швидкості. Б) Бистроту переміщення тіла. Д) Бистроту зміни кутової швидкості. В) Бистроту зміни модуля швидкості.
64. Що характеризує нормальне прискорення an?
А) Бистроту зміни вектора швидкості. Г) Бистроту зміни напрямку швидкості. Б) Бистроту переміщення тіла. Д) Бистроту зміни кутової швидкості. В) Бистроту зміни модуля швидкості.
65. Тангенціальне прискорення всіх точок тіла аt дорівнює нулю, а нормальне аn – постійне. Який цей рух?
А) Рівномірний обертальний. Б) Рівномірний прямолінійний. В) Рівнозмінний обертальний. Г) Рівнозмінний прямолінійний. Д) Рівномірний криволінійний.
66. Тіло рухається рівномірно по колу. Укажіть умову, при якій здійснюється цей рух? А) an=0, аt=0. Б) an=const, аt=0. В) an=const, аt=const. Г) an=0, аt=const. Д) an=f(t), аt=0.
67. Як залежить від часу нормальне прискорення an будь-якої точки твердого тіла, якщо тіло здійснює рівноприскорений обертальний рух? А) an~t2. Б) an~t. В) 68. Точка рухається рівноприскорено по колу. Якій умові відповідає цей рух?
А) an=0, аt=const. Б) an=const, аt=0. В) an~t2, аt=const. Г) an=0, аt~t2. Д) an~t, аt=const.
69. Який із випадків відповідає рівноприскореному обертальному рухові тіла?
А) аn=const, аt=0. Б) an=0, аt=const. В) an~ t, аt=const. Г) an~ t2, аt=const. Д) аn=const, аt=const.
70. Нормальне прискорення точок тіла an =0, а тангенціальне аt=const. Який цей рух?
А) Рівномірний прямолінійний. Б) Рівномірний обертальний. В) Рівнозмінний прямолінійний. Г) Рівномірний криволінійний. Д) Рівнозмінний обертальний.
71. Диск радіусом R =10 см обертається згідно із законом: j = 1+2t+t3. Чому дорівнює тангенціальне прискорення at точок на ободі диска через t =2 с після початку його руху? А) аt=5,4 м/с2. Б) аt=7,2 м/с2. В) аt=2,4 м/с2. Г) аt=3,6 м/с2. Д) аt=1,2 м/с2.
72. Диск радіусом R =10 см обертається згідно із законом: j = 1+2t+t3. Чому дорівнює нормальне прискорення аn точок на ободі диска через t =2 c після початку його руху? А) an=4,9 м/с2. Б) an=16,2 м/с2. В) an=9,8 м/с2. Г) an=19,6 м/с2. Д) an=12,4 м/с2.
73. Колесо радіусом R =0,2 м обертається так, що залежність кута повороту від часу задається рівнянням: j = 4+3t+2t3 рад. Знайти для точок, що лежать на ободі колеса, тангенціальне прискорення через t =2 c після початку його обертання.
А) аt=4,8 м/с2. Б) аt=7,2 м/с2. В) аt=8,1 м/с2. Г) аt=3,6 м/с2. Д) аt=6,4 м/с2.
74. Колесо радіусом R =0,2 м обертається так, що залежність кута повороту від часу задається рівнянням: j = 4+3t+2t3 рад. Знайти для точок, що лежать на ободі колеса, нормальне прискорення через t =2 c після початку його обертання.
А) аn=98 м/с2. Б) an=146 м/с2. В) аn=124 м/с2. Г) an=112 м/с2. Д) an=73 м/с2.
75. Матеріальна точка рухається по колу радіусу R =0,5 м так, що кут повороту її радіус-вектора змінюється за законом: j=2+3t+0,2t2. Розрахувати тангенціальне прискорення аt матеріальної точки через t =2 с після початку руху.
А) аt=0,8 м/с2. Б) аt=1,0 м/с2. В) аt=0,4 м/с2. Г) аt=0,6 м/с2. Д) аt=0,2 м/с2.
76. Матеріальна точка рухається по колу радіусу R =0,5 м так, що кут повороту її радіус-вектора змінюється за законом: j=2+3t+0,2t2. Розрахувати нормальне прискорення an матеріальної точки через t =2 с після початку руху.
А) аn=1,91 м/с2. Б) an=4,37 м/с2. В) аn=7,22 м/с2. Г) an=5,76 м/с2. Д) an=3,48 м/с2.
77. Точка рухається по колу радіусом R =2 м за законом: S = 2+3t2. Розрахувати тангенціальне прискорення аt точки через t =2 с після початку руху.
А) аt=15 м/с2. Б) аt=6 м/с2. В) аt=12 м/с2. Г) аt=18 м/с2. Д) аt=9 м/с2.
78. Точка рухається по колу радіусом R =2 м за законом: S = 2+3t2. Розрахувати нормальне прискорення an точки через t =2 с після початку руху. А) аn=54 м/с2. Б) an=144 м/с2. В) аn=36 м/с2. Г) an=72 м/с2. Д) an=118 м/с2.
79. Частинка рухається рівномірно по криволінійній траєкторії. Модуль її швидкості V =10 м/с. Знайти радіус кривини траєкторії R в тій точці, де модуль повного прискорення частинки а =10 м/с2.
А) 10,0 м. Б) 7,5 м. В) 12,5 м. Г) 5,0 м. Д) 2,5 м.
80. Автобус рухається по опуклому мосту. На середині моста його швидкість V =25 м/с, а нормальне (доцентрове) прискорення ац дорівнює прискоренню вільного падіння g. Який радіус R цього мосту?
А) 56 м. Б) 81 м. В) 64 м. Г) 72 м. Д) 48 м.
81. Кутова швидкість рівномірного обертання вітродвигуна w= 6 рад/с. Визначити нормальне (доцентрове) прискорення an кінців його лопаток, якщо їхня лінійна швидкість V =20 м/с.
А) 100 м/с2. Б) 140 м/с2. В) 160 м/с2. Г) 120 м/с2. Д) 80 м/с2.
82. Дві матеріальні точки рухаються по колах радіусів R1 та R2, причому R1 =2 R2. Порівняйте їх доцентрові прискорення (а1/а2), якщо періоди їх обертання Т однакові.
83. Колесо обертається із кутовим прискоренням e =2 рад/с2. Через t =0,5 c після початку руху нормальне прискорення точок на ободі колеса аn =1 м/с2. Визначити радіус цього колеса R. А) 2,0 м. Б) 0,5 м. В) 1,0 м. Г) 1,5 м. Д) 2,5 м.
84. Обчислити доцентрове прискорення аn лопаток вентилятора, якщо кутова швидкість його обертання w дорівнює 12 рад/с, а лінійна швидкість V кінців його лопаток складає 36 м/с.
А) 432 м/с2. Б) 218 м/с2. В) 326 м/с2. Г) 277 м/с2. Д) 384 м/с2.
85. Із якою швидкістю V автомобіль мусить проїжджати по опуклому мосту радіусом R =80 м, щоб у верхній точці мосту він знаходився у стані невагомості?
А) 20 м/с. Б) 32 м/с. В) 24 м/с. Г) 16 м/с. Д) 28 м/с.
86. Знайти доцентрове прискорення точок колеса автомобіля an, якщо він рухається зі швидкістю V =72 км/год, а частота n обертання колеса становить 4 Гц.
А) 392 м/с2. Б) 502 м/с2. В) 456 м/с2. Г) 278 м/с2. Д) 314 м/с2.
87. Чому дорівнює нормальне (доцентрове) прискорення аn потягу, що рухається рівномірно зі швидкістю V =20 м/с по заокругленню радіусом R =800 м?
А) 1,5 м/с2. Б) 2,5 м/с2. В) 1,0 м/с2. Г) 0,5 м/с2. Д) 2,0 м/с2.
88. Ротор турбіни, діаметром d =40 см, обертається з частотою n =200 Гц. Визначте нормальне (доцентрове) прискорення аn кінців лопаток турбіни.
А) 142 м/с2. Б) 286 м/с2. В) 194 м/с2. Г) 98 м/с2. Д) 251 м/с2.
89. По колу радіусом R =10 м рухається матеріальна точка. У деякий момент часу нормальне прискорення точки аn дорівнює 5 м/с2. Визначте швидкість точки V в цей момент часу. А) V=8,4 м/с. Б) V=6,8 м/с. В) V=7,1 м/с. Г) V=4,2 м/с. Д) V=5,6 м/с.
90. У деякий момент часу нормальне прискорення точки, яка рухається по колу, аn =5 м/с2. У цей момент кут j між повним і нормальним прискоренням становив 600. Визначте тангенціальне прискорення аt в цей момент часу.
А) аt=8,7 м/с2. Б) аt=4,3 м/с2. В) аt=3,2 м/с2. Г) аt=9,6 м/с2. Д) аt=6,4 м/с2.
Вільне падіння тіл
91. Значення яких величин необхідно знати для розрахунку прискорення вільного падіннятіла gh на будь-якій висоті від поверхні Землі?
А) R3, m, M3, h. Б) R3, M3, h, g. В) R3, h, g, m. Г) M3, m, g, h. Д) M3, m, g, R3..
92. За який проміжок часу t вільно падаюче тіло проходить перший сантиметр свого шляху? А) 30 мс. Б) 75 мс. В) 15 мс. Г) 60 мс. Д) 45 мс.
93. Чому дорівнює відношення шляхів, пройдених тілом за одну та за дві секунди після початку його вільного падіння h1/h2?
А) 0,75. Б) 0,45. В) 0,15. Г) 0,25. Д) 0,55.
94. Чому дорівнює відношення шляхів, які проходить тіло за три та за чотири секунди від початку його вільного падіння h3/h4?
95. Чому дорівнює відношення шляхів, пройдених тілом за чотири та за п'ять секунд від початку його вільного падіння h4/h5?
96. У деякий момент швидкість тіла, яке вільно падає, дорівнює V1 =7 м/с. Якою буде його швидкість V2 через Dt =1 c після цього? (Вважати g =10 м/с2).
А) 17 м/с. Б) 34 м/с. В) 21 м/с. Г) 28 м/с. Д) 14 м/с.
97. У скільки разів треба збільшити початкову швидкість V0 тіла, кинутого вертикально вгору, щоб час його підйому t збільшити вдвічі?
А) У 2,5 разів. Б) У 3,5 разів. В) У 4,0 рази. Г) У 2,0 рази. Д) У 1,5 рази.
98. На Місяці тіло, яке вільно падає, пролітає h =20 м за t =5 c. Визначте прискорення вільного падіння g на Місяці.
А) 8,7 м/с2. Б) 1,6 м/с2. В) 5,4 м/с2. Г) 3,2 м/с2. Д) 2,5 м/с2.
99. У скільки разів прискорення вільного падіння тіла gH на висоті H=2R3 менше, ніж g0 поблизу поверхні Землі? А) У 2 рази. Б) У 6 разів. В) У 9 разів. Г) У 4 рази. Д) У 3 рази.
100. На якій висоті Н від поверхні Землі сила тяжіння у 4 рази менша, ніж на поверхні Землі? Радіус Землі R3 вважати рівним 6400 км.
А) 3200 км. Б) 8100 км. В) 5400 км. Г) 1600 км. Д) 6400 км.
101. У скільки разів зменшиться вага тіла Р на висоті H, рівній радіусу Землі R3 у порівнянні із його вагою Р0 поблизу поверхні Землі?
А) У 2 рази. Б) У 1,5 рази. В) У 3 рази. Г) У 4 рази. Д) У 6 разів.
102. У скільки разів зменшиться вага тіла Р на висоті H=2R3 у порівнянні із його вагою Р0 поблизу поверхні Землі?
А) У 9 разів. Б) У 4 рази. В) У 2 рази. Г) У 6 разів. Д) У 3 рази.
103. На якій висоті h над полюсом Землі вага тіла Ph буде втричі меншою, ніж P0 на її поверхні? Радіус Землі вважати рівним R3 =6400 км.
А) 6,82×106 м. Б) 4,67×106 м. В) 41,3×107 м. Г) 3,8×106 м. Д) 6,4×105 м
104. М'яч, кинутий вертикально вгору, впав у вихідну точку через t =3 c. Із якою початковою швидкістю V0 його кинули? (Вважати g =10 м/с2).
А) 12 м/с. Б) 21 м/с. В) 15 м/с. Г) 9 м/с. Д) 18 м/с.
105. Тіло кинуте вертикально вгору із початковою швидкістю V0 =30 м/с. Через скільки секунд воно пролетіть повз позначку h =40 м у перший раз? (Вважати g =10 м/с2). А) 1,5 с. Б) 2,5 с. В) 3,0 с. Г) 2,0 с. Д) 3,5 с.
106. Тіло кинуте під кутом a =30° до горизонту із початковою швидкістю V0 =100 м/с. За який час тіло досягне висоти h =45 м у перший раз? (Вважати g =10 м/с2).
А) 0,25 с. Б) 1,25 с. В) 0,5 с. Г) 0,75 с. Д) 1,0 с.
107. Людина, яка знаходиться на вершині вежі висотою h =15 м, кидає вгору камінець із початковою швидкістю V0 =10 м/с. За який час t камінець досягне поверхні Землі? (Вважати g =10 м/с2).
А) 1,5 с. Б) 2,5 с. В) 3,0 с. Г) 2,0 с. Д) 3,5 с.
108. Літак летіть зі швидкістю V =450 км/год на висоті h =1960 м. Із нього треба скинути пакунок із поштою у пункт А. На якій відстані S від пункту А льотчик повинен скинути пакунок, щоб він точно потрапив у потрібне місце?
А) 1750 м. Б) 1250 м. В) 1500 м. Г) 2500 м. Д) 2250 м.
109. Вертоліт летить зі швидкістю V1 =180 км/год на висоті h =500 м. Із нього треба скинути деякий предмет на теплохід, який іде зустрічним курсом зі швидкістю V2 =24 км/год. На якій відстані S від теплоходу льотчик повинен це зробити?
А) 567 м. Б) 258 м. В) 684 м. Г) 456 м. Д) 324 м.
110. Краплина дощу починає вільно падати із хмари. За останню секунду перед падінням на землю вона пролетіла Dh =95 м. Визначте, скільки секунд летіла краплина? Опором повітря знехтувати. (Вважати g =10 м/с2).
А) 14 с. Б) 10 с. В) 16 с. Г) 8 с. Д) 12 с.
111. За умов попередньої задачі визначте, із якої висоти Н падала краплина?
А) 700 м. Б) 300 м. В) 900 м. Г) 1100 м. Д) 500 м.
112. Тіло кинуте з вежі горизонтально із початковою швидкістю V0 =15 м/с. На землю воно упало під кутом a =600 до горизонту. Визначте висоту вежі h.
А) 58,2 м. Б) 46,5 м. В) 27,8 м. Г) 34,4 м. Д) 61,7 м.
113. Тіло кинули горизонтально, і через t =5 с польоту кут a між напрямками його швидкості V та повного прискорення g склав 450. Зневажаючи опором повітря, обчисліть модуль швидкості тіла V в цей момент часу.
А) 82,4 м/с. Б) 48,6 м/с. В) 70,7 м/с. Г) 56,8 м/с. Д) 64,2 м/с.
114. Тіло падає без початкової швидкості із висоти Н =90 м. Зневажаючи опором повітря, обчисліть середню швидкість падіння Vcep на нижній половині шляху.
А) 36 м/с. Б) 24 м/с. В) 18 м/с. Г) 42 м/с. Д) 30 м/с.
115. Визначите кут a кидання тіла до горизонту, якщо максимальна висота підйому тіла Hmax дорівнює дальності S його польоту.
А) 490. Б) 580. В) 670. Г) 820. Д) 760.
116. Два тіла кинуті вертикально нагору із однієї точки з однаковою початковою швидкістю V0 =29,4 м/с через проміжок часу Dt =0,5 с. Через який час від моменту кидання першого тіла t вони зустрінуться?
А) 1,75 с. Б) 3,25 с. В) 2,25 с. Г) 2,75 с. Д) 3,75 с.
117. Два тіла кинуті вертикально нагору із однієї точки з однаковою початковою швидкістю V0 =29,4 м/с через проміжок часу Dt =0,5 с. На якій висоті h тіла зустрінуться? А) 38,6 м. Б) 51,7 м. В) 43,8 м. Г) 34,4 м. Д) 47,5 м.
118. Кулька вільно падає з висоти H =80 м. Визначте її переміщення Dh за останню секунду її руху. А) 40 м. Б) 25 м. В) 20 м. Г) 35 м. Д) 30 м.
119. Стріла, випущена з луку вертикально вгору, упала на землю через Dt =6 с. Обчисліть початкову швидкість стріли V0. (Вважати g =10 м/с2).
А) 20 м/с. Б) 35 м/с. В) 15 м/с. Г) 25 м/с. Д) 30 м/с.
120. Стріла, випущена із лука вертикально вгору, упала на землю через Dt =6 с. Обчисліть висоту її максимального підйому hmax. (Вважати g =10 м/с2).
А) 35 м. Б) 50 м. В) 45 м. Г) 30 м. Д) 40 м.
121. У шахту упав камінь. Людина почула звук від його падіння через t =6 с після початку падіння. Визначте глибину шахти h, якщо швидкість звука V у повітрі дорівнює 330 м/с.
А) 110 м. Б) 150 м. В) 70 м. Г) 90 м. Д) 130 м.
ОСНОВИ ТЕОРІЇ З РОЗДІЛУ “ДИНАМІКА МАТЕРІАЛЬНОЇ ТОЧКИ”
Причиною зміни стану руху тіла є його взаємодія із навколишніми тілами. Існує таке визначення фізики, як науки: фізика є вченням про різні типи взаємодій – гравітаційне, електромагнітне, сильне і слабке. Перші два види відомі людям досить добре. Гравітаційна взаємодія утримує, наприклад, планети при їх русі навколо зірок. Електромагнітна взаємодія утримує електрони, що обертаються навколо атомних ядер, і є основною між атомами і молекулами. Електромагнітні і гравітаційні взаємодії проявляють себе у макро- та мегасвіті, змінюються із відстанню як 1/r2 і є сильнодіючими – радіус їх дії необмежений. Дві останні взаємодії вимагають спеціальних методів досліджень. Сильні взаємодії – ядерні, зв'язують нуклони (протони і нейтрони) у ядрах хімічних елементів, а також утримують кварки усередині протона. Найбільша відстань, на якій проявляються сильні взаємодії (радіус їх дії) становить ~10-15 м. Слабкі взаємодії відповідальні за всі види b- розпаду нейтронів ядер, за багато процесів розпаду елементарних частинок, а також за всі процеси взаємодії нейтрино із речовиною. Слабкі взаємодії, як і сильні, є ще більш короткодіючими, радіус дії яких складає всього ~10-17 м. Для характеристики ступеня взаємодії тіл у фізиці вводиться фізична величина, звана силою. Сила – векторна фізична величина, яка служить мірою механічної дії на дане тіло з боку інших навколишніх тіл або полів, в результаті якого тіло або змінює своє положення у просторі, або змінює свою форму і розміри. У кожен момент часу сила характеризуються числовим значенням (модулем), напрямом у просторі і точкою додатку. Вимірюється сила по величині пружної деформації, а одиницею виміру сили служить Ньютон (Н). Розділ механіки, присвячений вивченню руху матеріальних тіл під дією прикладених до них сил, називають динамікою. У основі класичноїдинаміки – наукипро рух тіл – лежать три закони Ньютона, тому її часто називають ньютонівською. Закони сформульовані ним у 1667 році в праці «Математичні засади натуральної філософії» і є узагальненням численних дослідних даних. Оскільки взаємодія тіл припускає дію першого тіла на друге, і другого - на перше одночасно, то сила характеризує обидві дії відразу, тому зображається двома стрілками, прикладеними до обох тіл і спрямованими у протилежні сторони. Природно, що сили взаємодії між тілами мають однакову природу, завжди виникають парами і прикладені до різних (взаємодіючих) тіл. Це твердження про взаємність механічної дії тіл одне на одного у фізиці носить назву третього закону Ньютона, який формулюється так: два тіла при їх взаємодії діють одне на одного силами, які мають однакову природу, спрямованими уздовж однієї прямої, рівними за величиною і про-
тому вони не врівноважують одна одну. Взаємодії, які розглядаються законом, можуть бути як прямими або контактними (наприклад, при зіткненні тіл), так і непрямими або діями на відстані (наприклад, тяжіння Сонця і Землі). Цей закон дозволяє здійснити перехід від динаміки окремої матеріальної точки до динаміки системи точок, які взаємодіють попарно одна із одною. Другий закон Ньютона називають основним законом динаміки, оскільки він встановлює зв'язок між динамічними і кінематичними величинами. Окрім сили, іншою найважливішою динамічною характеристикою тіла служить його маса. Маса тіла – скалярна фізична величина, що є однією із основних характеристик матерії і визначає її інерційні (інертна маса) і гравітаційні (гравітаційна маса) властивості, а також її енерговміст. Інертністю тіла називають властивість, притаманна всім тілам і полягає у тому, що тіла чинять опір зміні своєї швидкості (як по модулю, так і по напрямку). Особливості гравітаційних взаємодій визначаються законом Всесвітнього тяжіння і будуть розглянуті нижче. Сьогодні можна визнати доведеним, що інертні і гравітаційні маси дорівнюють одна одній (із точністю, не меншою за 10-12 їхнього значення). Маса є адитивною величиною: маса складового тіла дорівнює сумі мас його частин. В межах класичної механіки, маса тіла є сталою величиною – не змінюється при русі цього тіла (зі швидкостями V<<c). Одиниця виміру маси – кілограм (кг). Другий закон Ньютона формулюється так: прискорення, якого набу-
У фізиці справедливий принцип незалежності дії сил: якщо на матеріальну точку (тіло) діє одночасно декілька сил, то кожна із них надає цій точці (тілу) прискорення, визначуване другим законом Ньютона, незалежно від дії решти сил. Тому прис-
прикладених сил. Сила завжди може бути розкладена на дві складові – тангенціаль-
мульований не через прискорення, а через імпульс тіла. Імпульсом матеріальної точки (тіла) називають векторну фізичну величину, яка чисельно дорівнює додатку маси цієї матеріальної точки (тіла) на її швидкість і має напрям швидкості: p=m × V. Одиниця виміру імпульсу – кілограм-метр в секунду (кг×м/с). Використавши визначення прискорення точки і визначення імпульсу, одержимо авторський вираз і фор-
може змінюватись із часом: швидкість зміни імпульсу матеріальної точки (тіла) дорівнює діючій на неї (нього) силі і відбувається у напрямку дії цієї сили. Записане рівняння ще називають рівнянням руху матеріальної точки. Перший закон Ньютона називається законом інерції. У формулюванні, приведеному Ньютоном, він був встановлений ще Галілеєм: будь-яка матеріальна точка (тіло) зберігає свій стан спокою або рівномірного прямолінійного руху доти, доки дія з боку інших тіл не примусить її змінити цей стан. Іншими словами, за відсутності зовнішніх дій (а, вірніше, при їх компенсації) тіло покоїться або рухається по прямій без зміни швидкості (за інерцією). У іншому формулюванні, цей закон звучить так: існують такі системи відліку, щодо яких поступально рухомі тіла зберігають свою швидкість постійною, якщо на них не діють інші тіла (або їхня дія компенсується). Системи відліку, щодо яких матеріальна точка, вільна від зовнішніх дій, або покоїться, або рухається рівномірно і прямолінійно, називаються інерціальними системами відліку. Твердження про існування інерціальних систем відліку складає зміст першого закону Ньютона – він виконується тільки в таких системах відліку. Системи відліку, рухомі із прискореннями щодо інерціальної системи відліку, називаються неінерціальними. Щоб передбачити характер руху тіла у кожному конкретному випадку, необхідно знати характер діючих на нього сил. У механіці вивчаються сили притягання (гравітаційні), сили пружності і сили тертя. 1. Сили притягання – це сили, які підкоряються закону Всесвітнього притягання, відкритого Ньютоном при вивченні руху небесних тіл на основі законів Кеплера і основних законів динаміки: між двома матеріальними точками із масами m1 і m2 діє сила взаємного притягання, пропорційна додатку їх мас і обернено пропорційна ква-
|

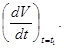 Б)
Б) 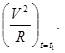 В)
В) 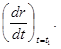 Г)
Г)  Д)
Д) 

 Б) аt=e×R. В) an=v2×R. Г) v=V×R. Д)
Б) аt=e×R. В) an=v2×R. Г) v=V×R. Д) 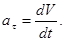
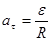 . Б) V=w×R. В)
. Б) V=w×R. В)  Г) w=w0±et. Д)
Г) w=w0±et. Д) 
 Б) аt=e×R. В)
Б) аt=e×R. В) 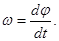 Г) an=V × w. Д) V=w2×R.
Г) an=V × w. Д) V=w2×R.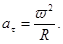 В)
В) 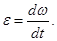 Г)
Г) 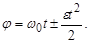 Д)
Д) 
 Г) an~
Г) an~ 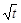 . Д)
. Д) 

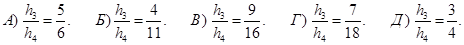




 - результуюча сила – геометрична сума всіх
- результуюча сила – геометрична сума всіх