
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Механика тела переменной массыСодержание книги
Поиск на нашем сайте
Механика тела переменной массы Механика жидкости (гидродинамика) Механика газа (газовая динамика, гидродинамика) Аксиомы механики: Первый закон Ньютона: Тело сохраняет свое состояние покоя, или равномерного прямолинейного движения, если на него не действует сил, или действие внешних сил уравновешено.
Второй закон Ньютона: Ускорение движущегося тела пропорционально равнодействующей всех внешних сил.
Третий закон Ньютона: Сила действия, равна силе противодействия. -> При изучении равновесия тел, рассматриваются только внешние силы, так как все внутренние силы уравновешены (скомпенсированы).
Аксиома связей: Связанное тело можно рассматривать как свободное, отбросив все внешние связи и заменив их действие реакциями.
Принцип независимости действия сил: Если на тело действуют различные силы, то действие каждой из них можно рассматривать независимо, а затем суммировать результаты.
Лекция 1. Статика. Основные понятия.
Сила - это мера взаимодействия тел. Сила - это векторная величина, она характеризуется направлением, величиной, точкой приложения. Если сила приложена в точке она называется сосредоточенной. Сила также может быть распределенной вдоль линии, по площадке или по объему (например сила тяжести). Если систему сил можно заменить другой системой сил, то они называются эквивалентными. Если система эквивалентна одной силе, то эта сила называется равнодействующей.
Проэкция силы на плоскость - это вектор, который идет от проэкции начала к Координатный способ представления
Системы сходящихся сил. Это такие силы, линии действия которых пересекаются в одной точке. Для
Условия равновесия системы сходящихся сил. Чтобы система сходящихся сил находилась в равновесии, нужно чтобы равнодействующая всех сил равнялась нулю. Геометрически это выражается в том, что силовой многоугольник должен быть замкнут. Аналитическое условие сумма проекций всех сил на каждую ось равна нулю.
Момент силы. Момент является количественной характеристикой вращательного эффекта
Момент силы на плоскости: плечо - расстояние от центра до силы. Момент равен произведению модуля силы на плечо, взятому с соответствующим знаком. (по часовой "-", против часовой "+".
Момент силы в пространстве: вращательный эффект силы в пространстве, зависит дополнительно от плоскости, в которой происходит вращение, поэтому
Произвольная система сил. В произвольной системе сил, суммарный поступательный эффект действия сил выражается в виде главного вектора системы и равен сумме всех сил, а суммарный вращательный эффект характеризуется главным моментом системы.
Условия равновесия.
Чтобы произвольная система сил в пространстве находилась в равновесии.
Аналитические условия равновесия произвольной пространственной системы сил. Сумма проэкций всех сил на все оси равны нулю, и сумма моментов относительно
Для произвольной плоской системы сил, имеем три уравнения равновесия. Дополнительные формы системы равновесии плоской системы сил. Лекция 2. Кинематика. Закон движения тела - это зависимость положения тела от времени. Формы задания законов движения. В зависимости от способа определения Векторная форма закона движения: Положение тела задается при помощи радиуса- вектора. Радиус вектор имеет начало в начале координат, а конец в точке. Координатная форма Положение тела определяется в декартовой системе координат.
Естественная форма
Координаты радиуса вектора являются координатами движущейся точки.
Для получения естественного нужно нужно взять производную от каждой координаты. А затем взять интеграл от суммы координат. Определение скорости точки. 1. Векторный способ Мгновенная скорость равна производен от дельты радиус вектора. Скорость направлена по касательной к траектории. 2.Координатный способ Скорость по каждой из координат находится, взятием производной от каждой из координат. Модуль вектора скорости равен корню квадратному из суммы по осям. При естественном способе скорость равна производной от S. Ускорение можно определить как скорость изменения скорости: 1. Векторный способ: ускорение находится как производная от скорости или вторая производная от радиус вектора. 2. В координатном способе ускорение есть первая производная от скорости или вторая производная по координате. Модуль ускорения равен квадратному корню из суммы ускорений по осям в квадратах. 3. В естественном способе ускорение раскладывается на две составляющие: нормальное(перпендикулярное касательной) и тангенсальное(направленное по
Сложное движение точки. Часто движение тела представляет собой наложение двух видов движения и его удобно рассматривать, как сложное движение. При этом вводиться подвижная система отсчета, которая является промежуточной между неподвижной системой отсчета и движущимся телом. Сложное (абсолютное) движение - это движение тела относительно неподвижной системы отсчета (земли). Переносное движение - это движение подвижной системы отсчета внутри неподвижной. Относительное движение - это движение тела в подвижной системе отсчета.
Анализ ускорения Кориолиса. Рассмотрим линейное движение точки вдоль радиуса вращающегося колеса. Пусть за время дельта Т точка М переместилась в положение М1, тогда линейная переносная скорость В(е)
Лекция 4. Динамика. Динамика изучает движение тел под действием сил. Основное уравнение динамики - это выражение второго закона Ньютона, то что ускорение тела пропорционально действию всех сил. В зависимости от формы записи закона движения существуют следующие формы основного уравнения динамики:
С помощью основного уравнения динамики можно решать две основных задачи.
Первая задача динамики: известен закон движения тела, требуется определить действующие силы. Первая задача динамики решается простым дифференцированием.
Вторая задача динамики: заданы действующие силы, требуется определить закон движения тела. Силы входящие в основное уравнение динамики могут зависеть от положения тела, от скорости, от времени и так далее. Поэтому решение второй задачи динамики сводится к интегрированию системы дифференциальных уравнений.
1. Начало отсчета выберем в положении статического равновесия, тогда сила Импульс. Импульсом называется произведением массы на скорость (для материальной точки). Для системы импульс определяется как сумма импульсов каждого движущегося тела.
Импульс силы. Закон изменения импульса за конечный промежуток времени. Изменения импульса за конечный промежуток времени, равно импульсу всех действующих сил в данный Удар - это такое движение, при котором за малый промежуток времени импульс изменяется на значительную величину. При ударе возникают силы очень большие по модулю, но действующие кратковременно, их часто называют импульсивными. В процессе исследования удара обычно пренебрегают всеми другими силам, так как они значительно меньше по уровню. Механика тела переменной массы Механика жидкости (гидродинамика) Механика газа (газовая динамика, гидродинамика) Аксиомы механики: Первый закон Ньютона: Тело сохраняет свое состояние покоя, или равномерного прямолинейного движения, если на него не действует сил, или действие внешних сил уравновешено.
Второй закон Ньютона: Ускорение движущегося тела пропорционально равнодействующей всех внешних сил.
Третий закон Ньютона: Сила действия, равна силе противодействия. -> При изучении равновесия тел, рассматриваются только внешние силы, так как все внутренние силы уравновешены (скомпенсированы).
Аксиома связей: Связанное тело можно рассматривать как свободное, отбросив все внешние связи и заменив их действие реакциями.
Принцип независимости действия сил: Если на тело действуют различные силы, то действие каждой из них можно рассматривать независимо, а затем суммировать результаты.
Лекция 1. Статика. Основные понятия.
Сила - это мера взаимодействия тел. Сила - это векторная величина, она характеризуется направлением, величиной, точкой приложения. Если сила приложена в точке она называется сосредоточенной. Сила также может быть распределенной вдоль линии, по площадке или по объему (например сила тяжести). Если систему сил можно заменить другой системой сил, то они называются эквивалентными. Если система эквивалентна одной силе, то эта сила называется равнодействующей.
Проэкция силы на плоскость - это вектор, который идет от проэкции начала к Координатный способ представления
Системы сходящихся сил. Это такие силы, линии действия которых пересекаются в одной точке. Для
Условия равновесия системы сходящихся сил. Чтобы система сходящихся сил находилась в равновесии, нужно чтобы равнодействующая всех сил равнялась нулю. Геометрически это выражается в том, что силовой многоугольник должен быть замкнут. Аналитическое условие сумма проекций всех сил на каждую ось равна нулю.
Момент силы. Момент является количественной характеристикой вращательного эффекта Момент силы на плоскости: плечо - расстояние от центра до силы. Момент равен произведению модуля силы на плечо, взятому с соответствующим знаком. (по часовой "-", против часовой "+".
Момент силы в пространстве: вращательный эффект силы в пространстве, зависит дополнительно от плоскости, в которой происходит вращение, поэтому
Произвольная система сил. В произвольной системе сил, суммарный поступательный эффект действия сил выражается в виде главного вектора системы и равен сумме всех сил, а суммарный вращательный эффект характеризуется главным моментом системы.
Условия равновесия.
Чтобы произвольная система сил в пространстве находилась в равновесии.
|
|||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 346; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.199.190 (0.01 с.) |

 Проэкция силы на ось:
Проэкция силы на ось: проэкции конца.
проэкции конца. силы:
силы:
 определения суммы сил используется правило силового многоугольника.
определения суммы сил используется правило силового многоугольника.
 Система сходящихся сил эквивалентна равнодействующей.
Система сходящихся сил эквивалентна равнодействующей. действия силы.
действия силы. момент силы относительно центра в пространстве представляется в виде вектора. Момент силы относительно центра в пространстве - это вектор равный по модулю произведению модуля силы на плечо и направленный перпендикулярно плоскости возможного вращения таким образом, что с конца вектора вращение видится против часовой стрелки. При сложном вращательном воздействии, результирующий момент равен векторной сумме
момент силы относительно центра в пространстве представляется в виде вектора. Момент силы относительно центра в пространстве - это вектор равный по модулю произведению модуля силы на плечо и направленный перпендикулярно плоскости возможного вращения таким образом, что с конца вектора вращение видится против часовой стрелки. При сложном вращательном воздействии, результирующий момент равен векторной сумме  моментов всех сил и называется главным моментом системы. При суммировании моментов геометрически можно использовать правило силового многоугольника.
моментов всех сил и называется главным моментом системы. При суммировании моментов геометрически можно использовать правило силового многоугольника. Главный вектор и главный момент системы должны равняются нулю.
Главный вектор и главный момент системы должны равняются нулю.
 всех осей равна нулю.
всех осей равна нулю. положения тела существует несколько форм записи закона движения.
положения тела существует несколько форм записи закона движения. Положение тела задается относительно траектории движения. Этот способ используется когда легко определить траекторию. Для этого вводится естественная координата S. Считаем траекторию координатной осью. Для координаты S выбирается начало и положительное направление, тогда координата определяется длинной дуги. Тогда закон движения имеет вид S=S(t).
Положение тела задается относительно траектории движения. Этот способ используется когда легко определить траекторию. Для этого вводится естественная координата S. Считаем траекторию координатной осью. Для координаты S выбирается начало и положительное направление, тогда координата определяется длинной дуги. Тогда закон движения имеет вид S=S(t). Связь между координатным и естественным способом.
Связь между координатным и естественным способом.  Рассмотрим изменение естественной координаты за малый промежуток времени и разложим его по проэкциям.
Рассмотрим изменение естественной координаты за малый промежуток времени и разложим его по проэкциям. Пример перехода к координатному способу.
Пример перехода к координатному способу. касательной). Модуль нормального ускорения равен частному квадрата скорости и радиуса кривизны траектории, а тангенсальное ускорение выражает изменение скорости по модулю.
касательной). Модуль нормального ускорения равен частному квадрата скорости и радиуса кривизны траектории, а тангенсальное ускорение выражает изменение скорости по модулю. изменится на величину. Тогда ускорение равно пределу отношения прикрашения функции к приращению аргумента. Таким образом скорость переносного движения изменяется по величине из-за наличия относительного движения. Рассмотрим изменение относительной скорости по направлению за время дельта Т.
изменится на величину. Тогда ускорение равно пределу отношения прикрашения функции к приращению аргумента. Таким образом скорость переносного движения изменяется по величине из-за наличия относительного движения. Рассмотрим изменение относительной скорости по направлению за время дельта Т. Оно имеет такую же величину, отсюда и удвоенный коэффициент. Скорость изменяется по направлению из-за наличия переносного и вращательного движения. Оба эти эффекта взаимного влияния переносного и относительного движений выражаются в ускорении Кориолиса.
Оно имеет такую же величину, отсюда и удвоенный коэффициент. Скорость изменяется по направлению из-за наличия переносного и вращательного движения. Оба эти эффекта взаимного влияния переносного и относительного движений выражаются в ускорении Кориолиса. - Векторная форма:
- Векторная форма: - Координатная форма:
- Координатная форма: - Естественная форма:
- Естественная форма: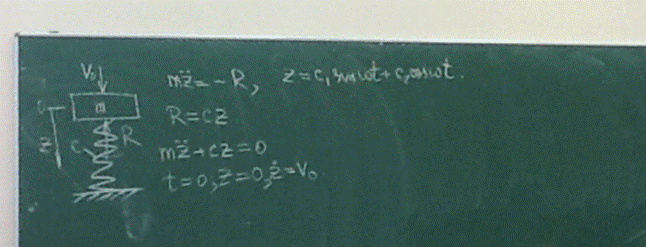 тяжести не входит.
тяжести не входит. Центр масс системы - это точка в которой можно считать сосредоточенной всю массы системы и которая движется как система в целом. Центр масс находится по правилу: масса систем умножите на радиус вектор центра масс.
Центр масс системы - это точка в которой можно считать сосредоточенной всю массы системы и которая движется как система в целом. Центр масс находится по правилу: масса систем умножите на радиус вектор центра масс. Закон сохранения импульса: постоянна.
Закон сохранения импульса: постоянна. период времени.
период времени.


