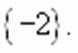Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Если возвести обе части уравненияСодержание книги
Поиск на нашем сайте
в натуральную степень
является следствием уравнения (1). Доказательство. - Если выполняется числовое равенство
- Если
Если Пример 1.
Ответ: Если в уравнение входят несколько радикалов, то их можно последовательно исключать с помощью возведения в квадрат, получая в итоге уравнение вида При этом полезно учитывать область допустимых значений исходного уравнения. Пример 2.
Ответ: Решение уравнений с использованием замены переменной Введение вспомогательной переменной в ряде случаев приводит к упрощению уравнения. Чаще всего в качестве новой переменной используют входящий в уравнение радикал. При этом уравнение становится рациональным относительно новой переменной. Пример 1.
Пусть тогда исходное уравнение примет вид: Решая уравнение получаем Ответ: В следующих примерах используется более сложная замена переменной. Пример 2
Перенесем в левую часть все члены уравнения и произведем дополнительные преобразования
Замена
Осталось решить совокупность двух уравнений:
Ответ: Метод разложения на множители выражений, Входящих в уравнение. Теорема. Уравнение
Пример 1.
При Ответ: Выделить общий множитель часто бывает очень трудно. Иногда это удается сделать после дополнительных преобразований. В приведенном ниже примере для этого рассматриваются попарные разности подкоренных выражений. Пример 2.
Если внимательно посмотреть на уравнение, то можно увидеть, что разности подкоренных выражений первого и третьего, а также второго и четвертого членов этого уравнения равны одной и той же величине В таком случае далее следует воспользоваться тождеством:
Уравнение примет вид:
Корень уравнения Уравнение Ответ:
|
|||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 128; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.205.21 (0.01 с.) |

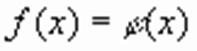 (1)
(1)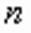 , то уравнение
, то уравнение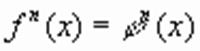 (2)
(2)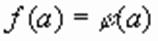 , то по свойствам степени выполняется равенство
, то по свойствам степени выполняется равенство 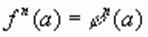 , т.е. каждый корень уравнения (1) является и корнем уравнения (2), это значит, что уравнение (2) является следствием уравнения (1).
, т.е. каждый корень уравнения (1) является и корнем уравнения (2), это значит, что уравнение (2) является следствием уравнения (1).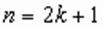 , то справедливо и обратная теорема. В этом случае уравнения (1) и (2) равносильны.
, то справедливо и обратная теорема. В этом случае уравнения (1) и (2) равносильны.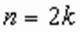 , равенство
, равенство 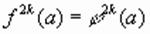 справедливо, если выполняется хотя бы одно из равенств
справедливо, если выполняется хотя бы одно из равенств 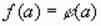 и
и 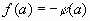 . Значит уравнения (1) и (2) в этом случае не равносильны. Поэтому, если в ходе решения иррационального уравнения
. Значит уравнения (1) и (2) в этом случае не равносильны. Поэтому, если в ходе решения иррационального уравнения 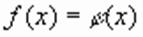 приходилось возводить обе его части в степень с четным показателем, то могли появиться посторонние корни. Чтобы отделить их, проверки можно избежать, введя дополнительное требование
приходилось возводить обе его части в степень с четным показателем, то могли появиться посторонние корни. Чтобы отделить их, проверки можно избежать, введя дополнительное требование 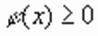 . В этом случае уравнение
. В этом случае уравнение 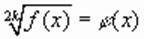 равносильно системе
равносильно системе 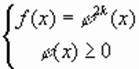 . В системе отсутствует требование
. В системе отсутствует требование 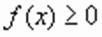 , обеспечивающее существование корня степени
, обеспечивающее существование корня степени 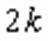 , т.к. оно было бы излишним в связи с равенством
, т.к. оно было бы излишним в связи с равенством  .
.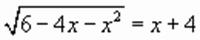
 ,
,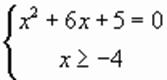 ,
,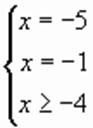 .
.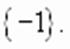

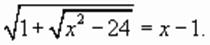

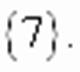
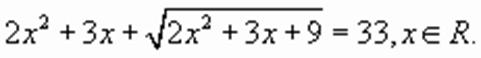
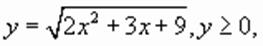
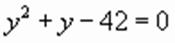 , корни которого
, корни которого 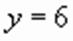 и
и 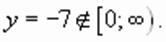
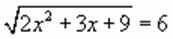 ,
,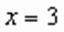 и
и 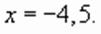
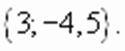
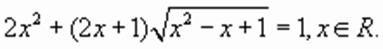
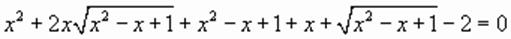 .
.
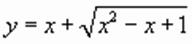 приводит уравнение к виду:
приводит уравнение к виду: корнями которого являются
корнями которого являются 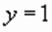 и
и 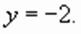
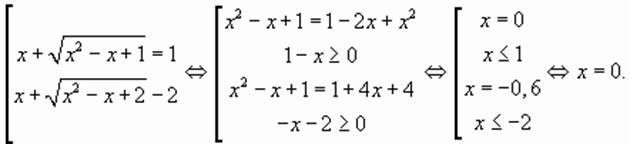
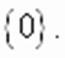
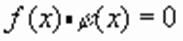 , определенное на всей числовой оси, равносильно совокупности уравнений
, определенное на всей числовой оси, равносильно совокупности уравнений 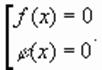
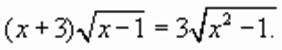
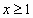 уравнение принимает вид:
уравнение принимает вид: 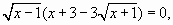 которое равносильно совокупности двух уравнений:
которое равносильно совокупности двух уравнений: 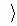
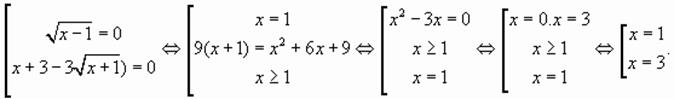
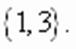

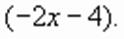

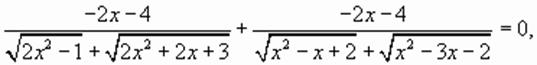 или
или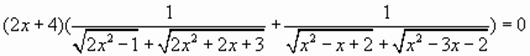
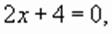 т.е. число
т.е. число  при подстановке в исходное уравнение дает верное равенство.
при подстановке в исходное уравнение дает верное равенство.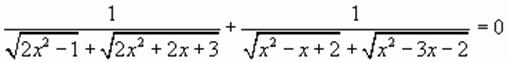 не имеет решений, так как его левая часть положительна в своей области определения.
не имеет решений, так как его левая часть положительна в своей области определения.