
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о случайном событии. Виды событий. Вероятность событияСтр 1 из 3Следующая ⇒
Основные понятия комбинаторики
Например,
Перестановки. Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками. Перестановки обозначаются символом Р n, где n- число элементов, входящих в каждую перестановку. Число перестановок можно вычислить по формуле
т.е. число всех возможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m. Запишем эту формулу в факториальной форме:
Сочетания.
Из этой формулы ясно, что
Заметим, что можно составить только одно сочетание из n элементов по n,которое содержит все n элементов. Формула числа сочетаний даёт это значение, если только принять, что 0! = 1,что является определением 0!. П р и м е р. Найти число сочетаний из пяти элементов: a, b, c, d, e по три. Р е ш е н и е:
Эти сочетания: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde. Бином Ньютона. Это формула, представляющая выражение (a + b) n при положительном целом n в виде многочлена:
Заметим, что сумма показателей степеней для a и b постоянна и равна n. П р и м е р 1.
Числа Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение: (a + b)7, мы можем получить результат моментально, используя таблицу:
Свойства биномиальных коэффициентов. 1. Сумма коэффициентов разложения (a + b) n равна 2 n. Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:
2. Коэффициенты членов, равноудалённых от концов разложения, равны. Это свойство следует из соотношения:
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна
Для доказательства воспользуемся биномом: Основные понятия математической статистики Основной целью математической статистики является установление закономерностей, которым подчиняются массовые случайные явления. Для этого решаются следующие основные задачи: определение способов сбора и обработки информации — результатов наблюдений. Пусть требуется определить наличие какого-либо признака, характеризующего объект, в большой совокупности однородных объектов. Например, это может быть дефект детали в большой партии одинаковых деталей. Для этого можно провести сплошное исследование всей партии деталей (совокупности). Однако часто такой подход оказывается невозможным по ряду причин. Во-первых, совокупность однородных объектов может быть очень большой, и тогда, анализ всей совокупности оказывается очень трудоемким. Во-вторых, исследование может быть очень дорогим или быть связано с разрушением объекта, и тогда, сплошное исследование становится бессмысленным. В таких случаях поступают по-другому: из всей совокупности отбирают некоторое число объектов и исследуют только их. Это число должно быть мало по сравнению со всей совокупностью, но достаточно велико, чтобы в этой отобранной группе уже начали проявляться статистические закономерности.
Введем основные понятия, использующиеся в математической статистике. Определение. Выборочной совокупностью (или выборкой) называют совокупность случайно отобранных объектов. Определение. Генеральной совокупностью называют совокупность всех объектов, из которых производится выборка. Определение. Объемом совокупности называют число объектов в этой совокупности. Пример Из 10000 деталей случайным образом выбирают 100 для исследования. Объем выборки — 100 деталей, объем генеральной совокупности — 10000 деталей. Выборку можно осуществлять различными способами. Если отобранный предмет после исследования возвращается в генеральную совокупность и снова может участвовать в отборе, то такую выборку называют повторной. Разумеется, такой способ возможен, когда объект не разрушается в результате исследования. Если отобранный предмет после исследования не возвращается в генеральную совокупность, то такую выборку называют бесповторной. Средняя арифметическая величина выборки Модой выборки называется значение, которое встречается наиболее часто. Медиа́на — число, характеризующее выборку (например, набор чисел). Если все элементы выборки различны, то медиана — это такое число выборки, что ровно половина из элементов выборки больше него, а другая половина меньше него. В более общем случае медиану можно найти, упорядочив элементы выборки по возрастанию или убыванию и взяв средний элемент. Например, выборка {11, 9, 3, 5, 5} после упорядочивания превращается в {3, 5, 5, 9, 11} и её медианой является число 5. Если в выборке чётное число элементов, медиана может быть не определена однозначно: для числовых данных чаще всего используют полусумму двух соседних значений (то есть медиану набора {1, 3, 5, 7} принимают равной 4), Размах выборки — разность между наибольшим и наименьшим значениями результатов наблюдений. Пример: Рост студентов: 153, 176, 189, 160, 173, 175, 155, 176, 164, 168. Найти среднее арифметическое, моду, медиану, размах выборки.
По смыслу выборки она должна быть мала по сравнению с генеральной совокупностью, поскольку иначе можно было бы проводить сплошное исследование. Именно такой случай малых выборок мы и будем в дальнейшем иметь в виду. Тогда, при возвращении объекта в генеральную совокупность после исследования, вероятность отобрать его снова мала и, фактически, нет разницы между повторной и бесповторной выборками. Поэтому в дальнейшем мы не будем конкретизировать способ выборки, а будем пользоваться более удобным способом в вычислениях. В определении выборки указывалось, что это совокупность случайно отобранных объектов. Задача случайного отбора не всегда является тривиальной и, в ряде случаев, требует специальных построений для того, чтобы отбор был действительно случайным. Кроме того, объем выборки должен быть достаточно большим, что бы начали проявляться закономерности обусловленные законом больших чисел. Такую выборку часто называют репрезентативной (представительной) выборкой
Применяют также и различные комбинации упомянутых выше способов отбора.Пусть из генеральной совокупности извлечена выборка из n объектов. Пусть значение некоторого признака объекта x1 наблюдалось n1 раз, x2 наблюдалось n2 раз и так далее. Разумеется,
Определение. Теоретической функцией распределения называют функцию распределения генеральной совокупности.Следует отметить, что относительная частота обладает всеми свойствами вероятности, статистическое распределение обладает всеми свойствами закона распределения, а эмпирическая функция распределения обладает всеми свойствами функции распределения случайной величины. В силу закона больших чисел, при больших n относительная частота, статистическое распределение и эмпирическая функция распределения будут близки к вероятности, закону распределения и функции распределения соответственно.Несложно обобщить данные понятия и на случай когда варианты принимают не дискретные, а непрерывные значения, нужно только под каждым xi понимать некоторый интервал значений.Для графического представления статистического распределения используют следующие инструменты. Математическая статистика изучает методы сбора, обработки и интерпретации результатов опытов (экспериментов). Генеральной совокупностью называют множество однородных объектов с характерными для них признаками. Выборочной совокупностью (выборкой) называют подмножество объектов генеральной совокупности, извлеченных из нее случайным образом. Случайная величина Статистические ряды Таблица 1
Таблица 2
Основные понятия комбинаторики
Например,
Перестановки. Комбинация из n элементов, которые отличаются друг от друга только порядком элементов, называются перестановками. Перестановки обозначаются символом Р n, где n- число элементов, входящих в каждую перестановку. Число перестановок можно вычислить по формуле
т.е. число всех возможных размещений из m элементов по n равно произведению n последовательных целых чисел, из которых большее есть m. Запишем эту формулу в факториальной форме:
Сочетания.
Из этой формулы ясно, что
Заметим, что можно составить только одно сочетание из n элементов по n,которое содержит все n элементов. Формула числа сочетаний даёт это значение, если только принять, что 0! = 1,что является определением 0!. П р и м е р. Найти число сочетаний из пяти элементов: a, b, c, d, e по три. Р е ш е н и е:
Эти сочетания: abc, abd, abe, acd, ace, ade, bcd, bce, bde, cde. Бином Ньютона. Это формула, представляющая выражение (a + b) n при положительном целом n в виде многочлена:
Заметим, что сумма показателей степеней для a и b постоянна и равна n. П р и м е р 1.
Числа Их можно вычислить, применяя только сложение, если пользоваться следующей схемой. В верхней строке пишем две единицы. Все последующие строки начинаются и заканчиваются единицей. Промежуточные числа в этих строках получаются суммированием соседних чисел из предыдущей строки. Эта схема называется треугольником Паскаля:
Первая строка в этой таблице содержит биномиальные коэффициенты для n = 1; вторая - для n = 2; третья - для n = 3 и т.д. Поэтому, если необходимо, например, разложить выражение: (a + b)7, мы можем получить результат моментально, используя таблицу:
Свойства биномиальных коэффициентов. 1. Сумма коэффициентов разложения (a + b) n равна 2 n. Для доказательства достаточно положить a = b = 1. Тогда в правой части разложения бинома Ньютона мы будем иметь сумму биномиальных коэффициентов, а слева:
2. Коэффициенты членов, равноудалённых от концов разложения, равны. Это свойство следует из соотношения:
3. Сумма коэффициентов чётных членов разложения равна сумме коэффициентов нечётных членов разложения; каждая из них равна
Для доказательства воспользуемся биномом: Понятие о случайном событии. Виды событий. Вероятность события
|
|||||||||||
|
Последнее изменение этой страницы: 2021-07-18; просмотров: 112; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.202.30 (0.054 с.) |
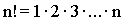







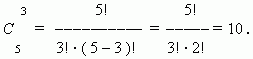
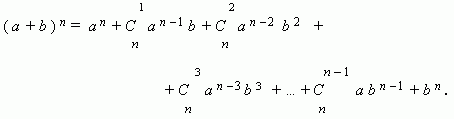
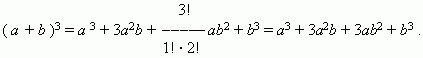
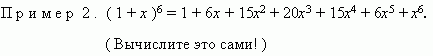
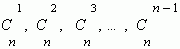 называются биномиальными коэффициентами.
называются биномиальными коэффициентами.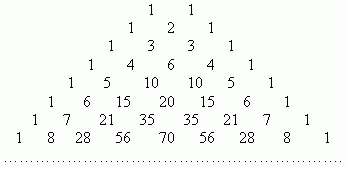
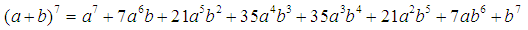
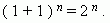
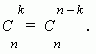

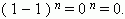 Здесь чётные члены имеют знак «+», а нечётные - «-». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна:
Здесь чётные члены имеют знак «+», а нечётные - «-». Так как в результате разложения получается 0, то следовательно, суммы их биномиальных коэффициентов равны между собой, поэтому каждая из них равна: 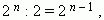 что и требовалось доказать.
что и требовалось доказать.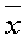 характеризует средний уровень значений изучаемой случайной величины в наблюдавшихся случаях и вычисляется путем деления суммы отдельных величин исследуемого признака на общее число наблюдений.
характеризует средний уровень значений изучаемой случайной величины в наблюдавшихся случаях и вычисляется путем деления суммы отдельных величин исследуемого признака на общее число наблюдений. .Чтобы обеспечить репрезентативность выборки, выделяют несколько способов отбора объектов.
.Чтобы обеспечить репрезентативность выборки, выделяют несколько способов отбора объектов.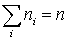 . Значения xi называются вариантами
. Значения xi называются вариантами 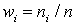 называют относительными частотами
называют относительными частотами 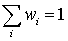 . Определение. Статистическим распределением выборки
. Определение. Статистическим распределением выборки 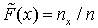 , где nx — число вариант со значением меньше x.
, где nx — число вариант со значением меньше x.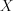 – наблюдаемые (полученные экспериментально) значения некоторого признака, характерного для всех объектов совокупности.
– наблюдаемые (полученные экспериментально) значения некоторого признака, характерного для всех объектов совокупности.




