Объем и его измерение. Интегральная формула объема. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра

МИНОБРНАУКИ РОССИИ

Федеральное государственное бюджетное образовательное учреждение

высшего образования

«Саратовский государственный технический университет имени Гагарина Ю.А.»

(СГТУ имени Гагарина Ю.А.)

ПРОФЕССИОНАЛЬНО-ПЕДАГОГИЧЕСКИЙ КОЛЛЕДЖ

 

 

РЕФЕРАТ по дисциплине

Математика

Тема: 1. «Объем и его измерение. Интегральная формула объема. Формулы объема куба, прямоугольного параллепипеда, призмы, цилиндры»

2. «Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади»

3. «Пособие тел. Отношение площадей поверхностей и объемов подобных тел.

4. «Практическая работа №9. Многогранники. Тела и поверхности вращения. Измерения в геометрии.»

 

 

Студент 1 курса

Группы СЭГ-911

Касимов Д.С.

Проверил: Рахманина И.Ю.

 

 

Саратов 2021 г

СОДЕРЖАНИЕ

Объем и его измерение. Интегральная формула объема. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра

Формула объема пирамиды и конуса. Формула площади поверхностей цилиндра и конуса. Формулы объема шара и площади

Подобие тел. Отношение площадей поверхностей и объемов подобных тел

Практическая работа №9. Многогранники. Тела и поверхности вращения. Измерения в геометрии

1 Объем и его измерение. Интегральная формула объема. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра.

Объем и его измерение

Длина, площадь, масса, время, объём - величины. Первоначальное знакомство с ними происходит в начальной школе, где величина наряду с числом является ведущим понятием.

ВЕЛИЧИНА - это особое свойство реальных объектов или явлений, и особенность заключается в том, что это свойство можно измерить, то есть назвать количество величины, которые выражают одно и тоже свойство объектов, называются ве­личинами одного рода или однородными величинами. Например, длина стола и дли на комнаты - это однородные величины. Величины - длина, площадь, масса и другие обладают рядом свойств.

1)Любые две величины одного рода сравнимы: они либо равны, либо одна меньше (больше) другой. То есть, для величин одного рода имеют место отношения «равно», «меньше», «больше» и для любых величин и справедливо одно и только одно из отношений: Например, мы говорим, что длина гипотенузы прямоугольного треугольника больше, чем любой катет данного треугольника; масса лимона меньше, чем масса арбуза; длины противоположных сторон прямоугольника равны.

2)Величины одного рода можно складывать, в результате сложения получится величина того же рода. Т.е. для любых двух величин а и b однозначно определяется величина a+b,её называют суммой величин а и b. Например, если a-длинаотрезка AB,b - длина отрезка ВС, то длина отрезка АС, есть сумма длин отрезков АВ и ВС;

.3)Величину умножают на действительное число, получая в результате величину того же рода. Тогда для любой величины а и любого неотрицательного числа x существует единственная величина b= x а, величину b называют произведением величины а на число x. Например, если a - длину отрезка АВ умножить на x= 2, то получим длину нового отрезка АС.

4) Величины данного рода вычитают, определяя разность величин через сумму:

разностью величин а и b называется такая величина с, что а=b+c. Например, если а - длина отрезка АС, b - длина отрезка AB, то длина отрезка ВС есть разность длин отрезков и АС и АВ.

5) Величины одного рода делят, определяя частное через произведение величины на число; частным величин а и b-называется такое неотрицательное действительное число х, что а= х b. Чаще это число - называют отношением величин а и b и записывают в таком виде: a/b = х. Например, отношение длины отрезка АС к длине отрезка АВ равно 2.(Рис №2).

6) Отношение «меньше» для однородных величин транзитивно: если А<В и В<С, то А<С. Так, если площадь треугольника F1 меньше площади треугольника F2 площадь треугольника F2 меньше площади треугольника F3, топлощадь треугольника F1 меньше площади треугольника F3.Величины, как свойства объектов, обладают ещё одной особенностью - их можно оценивать количественно. Для этого величину нужно измерить. Измерение - заключается в сравнении данной величины с некоторой величиной того же рода, принятой за единицу. В результате измерения

получают число, которое называют численным значением при выбранной единице.

Процесс сравнения зависит от рода рассматриваемых величин: для длин он один, для площадей - другой, для масс- третий и так далее. Но каким бы ни был этот процесс, в результате измерения величина получает определённое численное значение при выбранной единице.

Вообще, если дана величина а и выбрана единица величины e, то в результате измерения величины а находят такое действительное число x, что а=xe. Это число x называют численным значением величины а при единице е. Это можно записать так: х=m (a).

Согласно определению любую величину можно представить в виде произведения некоторого числа и единицы этой величины. Например, 7 кг = 7 1 кг, 12 см =12 1 см, 15ч =15 1 ч. Используя это, а также определение умножения величины на число, можно обосновать процесс перехода от одной единицы величины к другой. Пусть, например, требуется выразить 5/12ч в минутах. Так как, 5/12ч = 5/12 60мин = (5/12 60)мин = 25мин.

Величины, которые вполне определяются одним численным значением, называются скалярными величинами. Такими, к примеру, являются длина, площадь, объём, масса и другие. Кроме скалярных величин, в математике рассматривают ещё векторные величины. Для определения векторной величины необходимо указать не только её численное значение, но и направление. Векторными величинами являются сила, ускорение, напряжённость электрического поля и другие.

Объём и его измерение.

Понятие объёма определяется так же, как понятие площади. Но при рассмотрение понятия площадь, мы рассматривали многоугольные фигуры, а при рассмотрении понятия объём мы будем рассматривать многогранные Фигуры.

Объёмом фигуры называется неотрицательная величина, определённая для каждой Фигуры так, что:

1) равные фигуры имеют один и тот же объём;

2) если фигура составлена из конечного числа фигур, то её объём равен сумме их объёмов.

Условимся объём фигуры F обозначать V(F).

Чтобы измерить объем фигуры, нужно иметь единицу объёма. Как правило, за единицу объёма принимают объём куба с гранью, равной единичному отрезку e, то есть отрезку, выбранному в качестве единицы длины.

Если измерение площади сводилось к сравнению площади данной фигуры с площадью единичного квадрата e, то, аналогично, измерение объёма данной фигуры состоит в сравнении его с объёмом единичного куба е³ (рис.б). Результатом этого сравнения является такое число x,.что V(F)=х е.Число х называют численным значением объёма при выбранной единице объёма.

Так. если единицей объёма является 1 см, то объём фигуры, приведённой на рисунке 7, равен 4 см.

Объём фигуры и его измерение.

Программа по математике предусматривает наряду с рассмотренными величинами знакомство с объёмом и его измерением с помощью литра. Так же рассматривается объём пространственных геометрических фигур и изучаются такие единицы измерения объёма, как кубический сантиметр и кубический дециметр, а так же их соотношения.

Параллепипед

Параллелепипед (др.-греч. рбсбллзл-ерЯредпн; от др.-греч. рбс-Ьллзлпт -- «параллельный» и др.-греч.?рЯ-редпн -- «плоскость») -- призма, основанием которой служит параллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них -- параллелограмм.

Типы параллелепипеда:

Прямоугольный параллелепипед

Прямоугольный параллелепипед

Различается несколько типов параллелепипедов:

Прямоугольный параллелепипед -- это параллелепипед, у которого все грани -- прямоугольники. параллелепипед сторона поверхность грань

Прямой параллелепипед -- это параллелепипед, у которого 4 боковые грани прямоугольники.

Наклонный параллелепипед -- это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Ромбоэдр -- параллелепипед, грани которого являются равными ромбами.

Основные элементы.

Две грани параллелепипеда, не имеющие общего ребра, называются противоположными, а имеющие общее ребро -- смежными. Две вершины параллелепипеда, не принадлежащие одной грани, называются противоположными. Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда. Длины трёх рёбер прямоугольного параллелепипеда, имеющих общую вершину, называют его измерениями.

Свойства.

Параллелепипед симметричен относительно середины его диагонали.

Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

Противолежащие грани параллелепипеда параллельны и равны.

Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Основные формулы.

Прямой параллелепипед

Площадь боковой поверхности

S_б=РЧh

где Р -- периметр основания, h -- высота

Площадь полной поверхности S_п=S_б+2S_ос, где S_ос -- площадь основания

Объём

V=S_осЧh

Прямоугольный параллелепипед

Прямоугольный параллелепипед. Площадь боковой поверхности

S_б=2с(a+b)

где a, b -- стороны основания, c -- боковое ребро прямоугольного параллелепипеда

Площадь полной поверхности

S_п=2(ab+bc+ac)

Объём V=abc, где a, b, c -- измерения прямоугольного параллелепипеда.

Куб

Площадь поверхности: S=6a

Объём:

V=a³

где a -- ребро куба.

Произвольный параллелепипед

Объём и соотношения в наклонном параллелепипеде часто определяются с помощью векторной алгебры. Объём параллелепипеда равен абсолютной величине смешанного произведения трёх векторов, определяемых тремя сторонами параллелепипеда, исходящими из одной вершины. Соотношение между длинами сторон параллелепипеда и углами между ними даёт утверждение, что определитель. Грама указанных трёх векторов равен квадрату их смешанного произведения.

Призма

Рассмотрим произвольный многоугольник, например, пятиугольник АВСDЕ (см. чертеж на стр. 25), который лежит в плоскости a. Рассмотрим теперь параллельный перенос, определяемый некоторым ненулевым вектором V, не лежащим в плоскости. Образом плоскости a будет параллельная ей плоскость b. Образом многоугольника Ф будет многоугольник Ф1=A 1B 1C 1D 1E 1, лежащий в плоскости b. Направленные отрезки AA 1, BB 1 будут параллельны, так как каждый из них изображает один и тот же вектор V. Многогранник ABCDEA 1B 1C 1D 1E 1 называют призмой.

Определение 1. Многогранник, две грани которого - одноименные многоугольники, лежащие в параллельных плоскостях, а любые два ребра, не лежащие в этих плоскостях, параллельны, называется призмой.

Многоугольники Ф и Ф1, лежащие в параллельных плоскостях, называют основаниями призмы, а остальные грани - боковыми гранями.

Поверхность призмы, таким образом, состоит из двух равных многоугольников (оснований) и параллелограммов (боковых граней). Различают призмы треугольные, четырехугольные, пятиугольные и т.д. в зависимости от числа вершин основания.

Если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют прямой; если боковое ребро призмы перпендикулярно плоскости ее основания, то такую призму называют наклонной. У прямой призмы боковые грани - прямоугольники. Перпендикуляр к плоскостям оснований, концы которого принадлежат этим плоскостям, называют высотой призмы. На рис. отрезок A 1O - высота изображенной призмы.

Определение 2. Прямая призма, основанием которой служит правильный многоугольник, называется правильной призмой.

Боковое ребро прямой призмы, в том числе и правильной, есть ее высота. На рисунке изображена правильная шестиугольная призма и ее разверстка; высота этой призмы равна ее боковому ребру. Отрезок, концы которого - две вершины, не принадлежащие одной грани призмы, называют ее диагональю. Отрезок B 1D (см. рис.) - диагональ призмы. Сечение призмы с плоскостью, проходящей через два боковых ребра, не лежащих в одной грани, называют диагональным сечением призмы.

Площадь поверхности призмы

Поверхность многогранника состоит из конечного числа многоугольников (граней). Площадь поверхности многогранника есть сумма площадей всех его граней. Площадь поверхности призм (S пр) равна сумме площадей ее боковых граней (площади боковой поверхности S бок) и площадей двух оснований (2S осн) - равных многоугольников: S пр=S бок+2S осн.

Теорема. Площадь боковой поверхности призмы равна произведению периметра ее перпендикулярного сечения и длины бокового ребра.

Дано: АС 1 - произвольная n -угольная призма (на рисунке в качестве примера изображена четырехугольная призма), a^AA 1, A 2B 2C 2D 2 - перпендикулярное сечение (сечение призмы плоскостью, перпендикулярной боковому ребру), l - длина бокового ребра.

Доказать: S бок = Р Чl, где Р - периметр перпендикулярного сечения.

Доказательство. S бок= S AA 1B 1B + S BB 1C 1C + S CC 1D 1D +...

1444442444443

n слагаемых

Каждая боковая грань призмы - параллелограмм, основание которого - боковое ребро призмы, а высота - сторона перпендикулярного сечения.

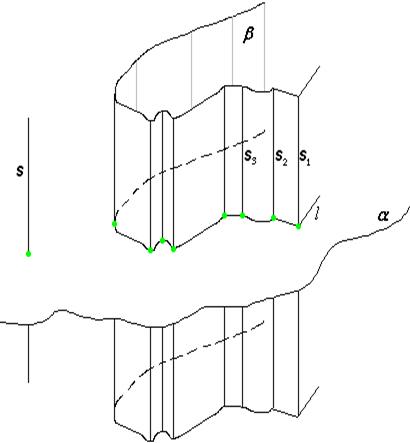
Поэтому

S бок=lA 2B 2+lB 2C 2+lC 2D 2+...=(A 2B 2+B 2C 2+C 2D 2+...)l =P Чl.

S бок = Р Чl.

Теорема доказана.

Следствие. Площадь боковой поверхности прямой призмы равна произведению периметра ее основания и высоты.

Действительно, у прямой призмы основание можно рассматривать как перпендикулярное сечение, а боковое ребро есть высота.

Призма и пирамида

Подобно тому, как треугольник в понимании Евклида не являются пустым, т. е. представляет собой часть плоскости, ограниченную тремя неконкурентными (т. е. не пересекающимися в одной точке) отрезками, так и многогранник у него не пустой, не полый, а чем-то заполненный (по-нашему - частью пространства). В античной математике, однако, понятия отвлеченного пространства еще не было. Евклид определяет призму как телесную фигуру, заключенную между двумя равными и параллельными плоскостями (основаниями) и с боковыми гранями - параллелограммами. Для того чтобы это определение было вполне корректным, следовало бы, однако, доказать, что плоскости, проходящие через пары непараллельных сторон оснований, пересекаются по параллельным прямым. Евклид употребляет термин “плоскость” как в широком смысле (рассматривая ее неограниченно продолженной во все направления), так и в смысле конечной, ограниченной ее части, в частности грани, аналогично применению им термина “прямая” (в широком смысле - бесконечная прямая и в узком - отрезок). В XVIII в. Тейлор дал такое определение призмы: это многогранник, у которого все грани, кроме двух, параллельны одной прямой.

Пирамиду Евклид определяет как телесную фигуру, ограниченную плоскостями, которые от одной плоскости (основания) сходятся в одной точке (вершине). Эго определение подвергалось критике уже в древности, например, Героном, предложившим следующее определение пирамиды: это фигура, ограниченная треугольниками, сходящимися в одной точке, и основанием которой служит многоугольник.

Важнейшим недостатком этого определения является использование неопределенного понятия основания. Тейлор определил пирамиду как многогранник, у которого все грани, кроме одной, сходятся в одной точке. Лежандр в “Элементах геометрии” так определяет пирамиду: “Телесная фигура, образованная треугольниками, сходящимися в одной точке и заканчивающаяся на различных сторонах плоского основания”. После этой формулировки разъясняется понятие основания. Определение Лежандра является явно избыточным, т.е. содержит признаки, которые можно вывести из других. А вот еще одно определение, которое фигурировало в учебниках ХIХ в.: пирамида - телесный угол, пересеченный плоскостью.

Еще в древности существовали два пути определения геометрических понятий. Первый вел от фигур высшего порядка к фигурам низшего. Такой точки зрения придерживался, в частности, Евклид, определяющий поверхность как границу тела, линию - как границу поверхности, концы же линии - как точки. Второй путь ведет, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично из линий составляется поверхность и т. д. Одним из первых, который соединил обе эти точки зрения, был Герон Александрийский, писавший, что тело ограничивается поверхностью и вместе с этим может быть рассмотрено как образованное движением поверхности. В появившихся позже на протяжении веков учебниках геометрии принималась за основу то одна, то другая, а иногда и обе вместе точки зрения.

Определение цилиндра

Рассмотрим какую-либо линию (кривую, ломаную или смешанную) l, лежащую в некоторой плокости α, и некоторую прямую S, пересекающую эту плоскость. Через все точки данной линии l проведем прямые, параллельные прямой S; образованная этими прямыми поверхность α называется цилиндрической поверхностью. Линия l называется направляющей этой поверхности, прямые s1, s2, s3,... − ее образующими.

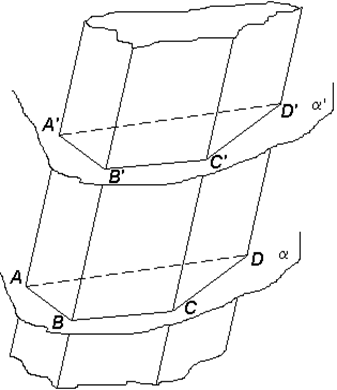
Если направляющая является ломаной, то такая цилиндрическая поверхность состоит из ряда плоских полос, заключенных между парами параллельных прямых, и называется призматической поверхностью. Образующие, проходящие через вершины направляющей ломаной, называются ребрами призматической поверхности, плоские полосы между ними − ее гранями.

Если рассечь любую цилиндрическую поверхность произвольной плоскостью, не параллельной ее образующим, то получим линию, которая также может быть принята за направляющую данной поверхности. Среди направляющих выделяется та, которая, получается, от сечения поверхности плоскостью, перпендикулярной образующим поверхности. Такое сечение называется нормальным сечением, а соответствующая направляющая − нормальной направляющей.

Если направляющая − замкнутая (выпуклая) линия (ломаная или кривая), то соответствующая поверхность называется замкнутой (выпуклой) призматической или цилиндрической поверхностью. Из цилиндрических поверхностей простейшая имеет своей нормальной направляющей окружность. Рассечем замкнутую выпуклую призматическую поверхность двумя плоскостями, параллельными между собой, но не параллельными образующим.

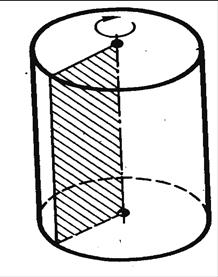
В сечениях получим выпуклые многоугольники. Теперь часть призматической поверхности, заключенная между плоскостями α и α', и две образовавшиеся при этом многоугольные пластинки в этих плоскостях ограничивают тело, называемое призматическим телом − призмой.

Цилиндрическое тело − цилиндр определяется аналогично призме:
Цилиндром называется тело, ограниченное с боков замкнутой (выпуклой) цилиндрической поверхностью, а с торцов двумя плоскими параллельными основаниями. Оба основания цилиндра равны, также равны между собой и все образующие цилиндра, т.е. отрезки образующих цилиндрической поверхности между плоскостями оснований.

Цилиндром (точнее, круговым цилиндром) называется геометрическое тело, которое состоит из двух кругов, не лежащих в одной плоскости и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих кругов (рис. 1).

Рис. 1 − Цилиндр

Элементы и свойства цилиндра

Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, − образующими цилиндра.

Так как параллельный перенос есть движение, то основания цилиндра равны.

Так как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у цилиндра основания лежат в параллельных плоскостях.

Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у цилиндра образующие параллельны и равны.

Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.

Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.

Прямой цилиндр наглядно можно представить себе как геометрическое тело, которое описывает прямоугольник при вращении его около стороны как оси (рис. 2).

Рис. 2 − Прямой цилиндр

В дальнейшем мы будем рассматривать только прямой цилиндр, называя его для краткости просто цилиндром.

Радиусом цилиндра называется радиус его основания. Высотой цилиндра называется расстояние между плоскостями его оснований. Осью цилиндра называется прямая, проходящая через центры оснований. Она параллельна образующим.

Цилиндр называется равносторонним, если его высота равна диаметру основания.

Если основания цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости цилиндра перпендикулярны образующей, то цилиндр называется прямым.

В частности, если основание стоящего на плоскости цилиндра − круг, то говорят о круговом (круглом) цилиндре; если эллипс − то эллиптическом.

Определение понятия

Пирамида - это многогранник, у которого одна грань (основание пирамиды) - это произвольный многоугольник (ABCDE, рис.80), а остальные грани (боковые грани) - треугольники с общей вершиной S, называемой вершиной пирамиды. Перпендикуляр SO, опущенный из вершины пирамиды на её основание, называется высотой пирамиды. В зависимости от формы многоугольника, лежащего в основании, пирамида может быть соответственно: треугольной, четырёхугольной, пятиугольной, шестиугольной и т.д. Треугольная пирамида является тетраэдром (четырёхгранником), четырёхугольная - пятигранником и т.д. Пирамида называется правильной, если в основании лежит правильный многоугольник, а её высота падает в центр основания. Все боковые рёбра правильной пирамиды равны; все боковые грани - равнобедренные треугольники. Высота боковой грани (SF) называется апофемой правильной пирамиды.

Если провести сечение abcde, параллельное основанию ABCDE (рис.81) пирамиды, то тело, заключённое между этими плоскостями и боковой поверхностью, называется усеченной пирамидой. Параллельные грани ABCDE и abcde называются основаниями; расстояние Oo между ними - высотой. Усечённая пирамида называется правильной, если пирамида, из которой она была получена - правильная. Все боковые грани правильной усечённой пирамиды - равные равнобочные трапеции. Высота Ff боковой грани (рис.81) называется апофемой правильной усечённой пирамиды.

Пирамидой называется тело, образованное плоским многоугольником (основание), точкой, нележащей в плоскости этого многоугольника (вершина), и всех отрезков, соединяющих точки основания с вершиной.

Стороны многоугольника есть ребра основания. Прямые, соединяющие вершины основания с вершиной трапеции, есть боковые ребра. Совокупности прямых, соединяющих каждую по отдельности сторону основания с вершиной, называются боковыми гранями.

Пирамиды классифицируются по числу сторон многоугольника, лежащего в их основании. Говорят о треугольной, четырехугольной и вообще n-угольной пирамидах.

Заметим, что n-угольная пирамида имеет n+1 граней: n боковых граней и основание. При вершине пирамиды мы имеем n-гранный угол с n плоскими и n двугранными углами. Они соответственно называются плоскими углами при вершине и двугранными аглами при боковых ребрах. При вершинах основания мы имеем n трехгранных углов; их плоские углы, образованные боковыми ребрами и сторонами основания, называются плоскими углами при основании, двугранные углы между боковыми гранями и плоскостью основания - двугранными углами при основании.

Треугольная пирамида иначе называется тетраэдром (т.е. четырехгранником). Особенность тетраэдра в том, что любая из его граней может быть принята за основание.

Пирамида называется правильной, если в её основании лежит правильный многоугольник, а высота, опущенная из вершины пирамиды на основание, пересекает его в центре этого многоугольника (иначе говоря, вершина пирамиды проектируется в центр основания).

Заметим, что правильная пирамида не является, вообще говоря, правильным многогранником.

Отметим некоторые свойства правильной n-угольной пирамиды на примере треугольной пирамиды. Как известно центр правильного треугольника совпадает с центром вписанной и описанной окого него окружности. Поэтому отрезки АО, ВО и СО равны как радиусы.

Поэтому прямоугольные треугольники АОМ, ВОМ и СОМ равны по двум катетам (МО-общая). Из равенства этих треугольников следует равенство соответствующих сторон: АМ=ВМ=СМ

Свойство 1 В правильной n-угольной пирамиде все боковые ребра равны между собой.

Из равенства ребер следует и равенство боковых граней. Треугольники АВМ, ВСМ и АСМ равны по трем сторонам.

Свойство 2 Все боковые грани правильной n-угольной пирамиды суть равные равнобедренные треугольники, поэтому все плоские углы при вершине равны, все плоские углы при основании равны.

Из равенства прямоугольных треугольников ОРМ, ОТМ и ОКМ (ОТ=ОР=ОК как радиусы вписанной окружности; МО - общая) следует равенство всех двугранных углов при основании пирамиды РОРМ=РОТМ=РОКМ

Свойство 3 В правильной n-угольной пирамиде все двугранные углы при основании равны.

Нужно отметить случай, когда одно из боковых ребер пирамиды перпендикулярно основанию. Такая пирамида называется прямоугольной.

Апофема - высота боковой грани пирамиды, проведенная из вершины на ребро основания.

Теорема 1. Если все боковые грани пирамиды наклонены к плоскости основания под одинаковым углом, то в основание такой пирамиды можно вписать круг, а высота, опущенная из вершины на основание, падает в центр вписанного в основание круга. Эту теорему можно сформулировать и так: Если все апофемы (высоты боковых граней) пирамиды равны, то в основание такой пирамиды можно вписать круг, а высота, опущенная из вершины на основание, падает в центр вписанного в основание круга.

Доказательство. Докажем теорему на при мере треугольной пирамиды. Пусть дана пирамида ABCM, М -вершина, АВС - основание, МО - высота пирамиды. В боковой грани АМВ проведем высоту МК. В плоскости основания соединим точку О (основание высоты) с точкой К. ОК перпендикулярна АВ (по теореме о трех перпендикулярах, где МК - наклонная, ОК её проекция на плоскость и АВ - прямая в плоскости). По определению угол МКО-линейный угол двугранного угла между плоскостью МАВ и основанием ABC. Таким же образом проведем высоты МР и МТ соответственно в боковых гранях МВС и MAC и докажем, что углы МРО и МТО - линейные углы двугранных углов, образованных соответствующими боковыми гранями МВС и MAC с основанием ABC. По условию углы МКО, МРО и МТО равны. Рассмотрим треугольники МКО, МРО и МТО, они прямоугольны и равны (по катету и острому углу, МО - общая и углы МКО, МРО и МТО равны по условию). Из равенства этих треугольников следует, что их соответствующие стороны ОК, ОР и ОТ равны, а значит, в треугольнике ABC есть такая точка, которая равноудалена от сторон треугольника, то есть в него можно вписать круг. Для второго случая (равенства апофем) доказательство изменится только в том месте, где говорится, что треугольники равны по катету и углу. Это место надо поменять на: треугольники равны по катету и гипотенузе (МО - общая, МТ=МР=МК - апофемы).

Теорема 2. Если все боковые ребра пирамиды наклонены к плоскости основания под одинаковым углом, то около основания такой пирамиды можно описать окружность, а высота, опущенная из вершины на основание, падает в центр описанной около основания окружности. Эту теорему можно сформулировать и так: Если все боковые ребра пирамиды равны, то около основания такой пирамиды можно описать окружность, а высота, опущенная из вершины на основание, падает в центр описанной около основания окружности.

Доказательство. Докажем теорему на при мере треугольной пирамиды. Пусть дана пирамида ABCM, М - вершина, ABC - основание, МО - высота пирамиды. В плоскости основания соединим точку О (основание высоты) со всеми вершинами основания А, В и С. Угол МВО - угол между ребром MB и плоскостью основания (угол между прямой и плоскостью есть угол между этой прямой и её проекцией на эту плоскость). Таким же образом докажем, что углы МСО и МАО - углы, образованные соответствующими ребрами МС и МА с плоскостью основания. Углы МВО, МСО и МАО равны по условиям теоремы.

Рассмотрим треугольники МВО, МСО и МАО, они прямоугольны и равны (по катету и острому углу, МО - общая и углы МВО, МСО и МАО равны по условию). Из равенства этих треугольников следует, что их соответствующие стороны ОВ, ОС и ОА равны, а значит, в основании есть такая точка, которая равноудалена от вершин треугольника ABC, то есть около него можно описать окружность. Для второго случая (равенства боковых ребер) доказательство изменится только в том месте, где говорится, что треугольники равны по катету и углу. Это место надо поменять на: треугольники равны по катету и гипотенузе (МО - общая, МА=МВ=МС - боковые ребра).

площадь пирамида многоугольник плоскость

Объем пирамиды

Определение

Конусом (точнее, круговым конусом) называется тело, которое состоит из круга - основания конуса, точки, не лежащей в плоскости этого круга, - вершины конуса и всех отрезков, соединяющих вершину конуса с точками основания (рис. 1) Отрезки, соединяющие вершину конуса с точками окружности основания, называются образующими, конуса. Поверхность конуса состоит из основания и боковой поверхности.

Конус называется прямым, если прямая, соединяющая вершину конуса с центром основания, перпендикулярна плоскости основания. В дальнейшем мы будем рассматривать только прямой конус, называя его для краткости просто конусом. Наглядно прямой круговой конус можно представлять себе как тело, полученное при вращении прямоугольного треугольника вокруг его катета как оси.

Высотой конуса называется перпендикуляр, опущенный из его вершины на плоскость основания. У прямого конуса основание высоты совпадает с центром основания. Осью прямого кругового конуса называется прямая, содержащая его высоту.

Теорема

Плоскость, параллельная плоскости основания конуса, пересекает конус по кругу, а боковую поверхность - по окружности с центром на оси конуса.

Доказательство. Пусть - плоскость, параллельная плоскости основания конуса и пересекающая конус (рис. 5). Преобразование гомотетии относительно вершины конуса, совмещающее плоскость с плоскостью основания, совмещает сечение конуса плоскостью с основанием конуса.

Следовательно, сечение конуса плоскостью есть круг, а сечение боковой поверхности - окружность с центром на оси конуса. Теорема доказана.

Сечение

Сечение конуса плоскостью, проходящей через его вершину, представляет собой равнобедренный треугольник, у которого боковые стороны являются образующими конуса. В частности, равнобедренным треугольником является осевое сечение конуса. Это сечение, которое проходит через ось конуса.

Усеченным конусом называется часть конуса, ограниченная его основанием и сечением, плоскость которого параллельна плоскости основания.

1. Боковая поверхность

Площадь (S) боковой поверхности конуса равняется произведению числа π на радиус основания и на длину образующей.

Sбок. = πR l

Образующая (l) соединяет вершину конуса и границу основания, другими словами, точку на окружности. Примечание: в вычислениях значение числа π округляется до 3,14.

2. Основание. Основанием конуса является круг, площадь которого вычисляется так:

 Sосн. = πR2

Учитывая то, что диаметр круга равняется двум его радиусам (d = 2R), данную формулу можно представить в виде:

Sосн. = π(d/2)2

Объем шара

Объём шара равен 4/3 π на произведение радиуса (r) в кубе

V =

где:V - объем шара, π - число пи (3.1415), R - радиус шара

Формула объема шара через радиус: Объем шара V вычисляется по формуле (см. ниже), где R — радиус шара, число «пи» — π — математическая константа, ≈ 3,14.

V = 4/(3)*π*R³

Измерения в геометрии

 Геометрические величины
Геометрические величины - это свойства геометрических фигур, характеризующие их форму и размеры. К ним относятся: длина, площадь, объем и величина угла.
В геометрии, прежде всего, изучают то число, которое получается в результате измерения величины, то есть меру величины при выбранной единице величины. Поэтому часто число называют длиной, площадью, объемом. Относительно этого числа решают различные теоретические задачи. Вообще правила измерения геометрических величин и их обоснование - важнейшая задача геометрии.

Длина

Отрезок - это часть прямой линии, ограниченная двумя точками - началом и концом.
А длина отрезка это расстояние от одной точки до другой. Определить длину отрезка возможно разными способами:

1. Длина отрезка с помощью линейки - для этого прикладываем к построенному на плоскости отрезку линейку с миллиметровыми делениями, причем начальную точку необходимо совместить с нулем шкалы линейки. Затем следует отметить на данной шкале расположение конечной точки данного отрезка. Полученное количество целых делений шкалы и будет являться длиной отрезка, выраженной в см. и мм.

2. Метод координат на плоскости - если известны координаты отрезка (х1;у1) и (х2;у2), то следует рассчитать его длину следующим образом. Из координат на плоскости второй точки следует вычесть координаты первой точки. В итоге должно получиться два числа. Каждое из таких чисел необходимо возвести в квадрат, а потом найти сумму этих квадратов. Из полученного числа следует извлечь квадратный корень, который будет являться расстоянием между точками. Поскольку данные точки являются концами отрезка, то данное значение и будет его длиной.

3. Метод координат в пространстве – нужно найти длину вектора, для этого:
Найдите координаты вектора, для этого из координат его конечной точки нужно вычесть координаты его начальной точки.

После этого нужно возвести каждую координату вектора в квадрат. Затем складываем квадраты координат. Чтобы найти длину вектора, нужно извлечь квадратный корень из суммы квадратов координат. Получили длину вектора, именно она и является отрезком в евклидовом пространстве. Площадь фигуры и ее измерение.

Площадь - это величина, которая указывает, сколько места занимает фигура на плоскости.

В качестве общепринятых единиц измерения площадей используют квадраты со сторонами 1 см, 1 дм, 1 м. Эти измерения соответственно называют: квадратный сантиметр – 1 см²;квадратный дециметр –
1 дм²;квадратный метр – 1 м².
Как можно сравнить площади фигур:
- «на глаз»;
- наложением;
- с помощью мерки;

Чтобы измерить площадь фигуры, нужно иметь единицу площади. Как правило, токай единицей является площадь квадрата со стороной, равному единичному отрезку.

Условимся площади единичного квадрата обозначать буквой Е, а число, которое получается в результате измерения площади фигуры –S (F). Это число называют численным значением площади фигуры F при выбранной единице площади Е. Оно должно удовлетворять условиям:

1. Число S(F) – положительное.

2. Если фигуры равны, то равны числовые значения из площадей.