Этапы решения задач на компьютере. Решение задач в любой сфере деятельности – это всегда получение определенных

Решение задач в любой сфере деятельности – это всегда получение определенных результатов. А процесс получения результатов опирается на некоторый способ действий и предполагает использование определенных средств. Одним из новейших средств решения различных задач становятся современные компьютеры – универсальные устройства обработки и накопления данных.

 

Универсальность компьютеров состоит в том, что они могут обрабатывать любые данные и решать задачи в любой предметной области.

 

Решение задачи на компьютере происходит в несколько этапов.

 

Й этап – постановка задачи.

 

На данном этапе строится описательная информационная модель объекта или процесса. Поиск решения любой задачи начинается с анализа ее условий. Результатом анализа должна стать четкая постановка задачи, в которой должны быть ответы на четыре вопроса:

 Что дано?

 Что требуется?

 Какие данные допустимы?

 Какие результаты будут правильными, а какие нет?

Й этап – разработка математической модели.

 

Правильность результатов решения задачи с помощью компьютера зависит, прежде всего, от правильности выбранного метода решения. Метод решения является правильным, если для любых допустимых исходных данных он приводит к получению результатов, соответствующих постановке задачи. Для решения задач с помощью компьютера соответствующим методам необходимо дать математическую интерпретацию. Как правило, строится математическая модель задачи. Создавая математическую модель, нужно записать математические соотношения (формулы, уравнения, неравенства и т.д.), связывающие результаты с исходными данными.

3-му этап – конструирование алгоритма на основе математической модели.

 

О понятии алгоритма и его свойствах, о типах алгоритмов и способах их конструирования мы поговорим позже.

4-й этап – перевод алгоритма в программу.

 

Дальнейшее исследование информационной модели, записанной в форме алгоритма, можно проводить на компьютере различными способами. Можно закодировать алгоритм на языке программирования (Basic, Pascal и т.д.) или воспользоваться специальным программным приложением (электронные таблицы, СУБД).

5-й этап – проведениикомпьютерного эксперимента.

 

Если мы исследуем информационную модель в виде программы в какой-либо среде программирования, то к этому этапу относятся:

 запуск выбранной среды программирования;

 набор текста программы;

 сохранение этого текста на диске;

 запуск программы на выполнение.

 

Причем необходимо запускать программу на выполнение многократно – при различных значениях начальных условий.

Можно воспользоваться и готовыми программными средствами. Так, например, если информационная модель исследуется в электронных таблицах, то различные числовые данные вводятся в соответствующие ячейки.

 

6-й этап – анализ получаемых результатов и корректировке исследуемой модели.

 

Алгоритм

Алгоритм – система точных и понятных предписаний (команд, инструкций, директив) о содержании и последовательности выполнения конечного числа действий, необходимых для решения любой задачи данного типа. Как всякий объект, алгоритм имеет название (имя). Также алгоритм имеет начало и конец.

Понятие алгоритма в информатике является фундаментальным, т. е. таким, которое не определяется через другие, более простые понятия.

Исполнитель алгоритмов.

Задача составления алгоритма не имеет смысла, если не известны или не учитываются возможности его исполнителя, ведь выполнимость алгоритма зависит от того, какие действия может совершить исполнитель (СКИ – система команд исполнителя).

Например, прочесть алгоритм решения уравнения сможет и первоклассник, а выполнить его, конечно же, нет.

С другой стороны, малыш трех лет не сможет прочесть правила (алгоритм) поведения за столом во время еды, но выполнить их сможет, если ему о них рассказать и показать, что они обозначают.

Команда алгоритма правильна, если исполнитель ее понял и умеет выполнить.

Кто может являться исполнителем алгоритмов?

В качестве исполнителя алгоритмов можно рассматривать человека, любые технические устройства, среди которых особое место занимает компьютер. Компьютер может выполнять только точно определенные операции, в отличии от человека, получившего команду: «Купи чего-нибудь вкусненького» и имеющего возможность сориентироваться в ситуации.

Алгоритм обладает следующими свойствами.

1. Дискретность (от лат. discretus – разделенный, прерывистый) указывает, что любой алгоритм должен состоять из конкретных действий, следующих в определенном порядке. Образованная структура алгоритма оказывается дискретной: только выполнив одну команду, исполнитель сможет приступить к выполнению следующей.

2. Детерминированность (от лат. determinate – определенность, точность) указывает, что любое действие алгоритма должно быть строго и недвусмысленно определено в каждом случае. При этом каждая команда алгоритма входит в состав системы команд исполнителя.

3. Конечность определяет, что каждое действие в отдельности и алгоритм в целом должны иметь возможность завершения.

4. Результативность требует, чтобы в алгоритме не было ошибок, т.е. при точном исполнении всех команд процесс решения задачи должен прекратиться за конечное число шагов и при этом должен быть получен определенный постановкой задачи результат (ответ).

5. Массовость. Это свойство показывает, что один и тот же алгоритм можно использовать с разными исходными данными, т.е. применять при решении всего класса задач данного типа, отвечающих общей постановке задачи. Пример: алгоритмы «Решение квадратного уравнения», «Приготовить бутерброд».

Тип алгоритма определяется характером решаемой (в соответствии с его командами) задачи.

Типовые конструкции алгоритмов:

· Линейная.

· Циклическая.

· Разветвляющаяся.

· Вспомогательная.

Линейный (последовательный) алгоритм – описание действий, которые выполняются однократно в заданном порядке.

Циклический – описание действий или группы действий, которые должны повторяться указанное число раз или пока не выполнено заданное условие. Совокупность повторяющихся действий – тело цикла.

Разветвляющийся – алгоритм, в котором в зависимости от условия выполняется либо одна, либо другая последовательность действий. Условие – выражение, находящееся между словом «если» и словом «то» и принимающее значение «истина» (ветвь «да») или «ложь» (ветвь «нет»). Возможна полная и неполная форма ветвления.

Вспомогательный – алгоритм, который можно использовать в других алгоритмах, указав только его имя. Вспомогательному алгоритму должно быть присвоено имя.

Способы описания алгоритмов.

· на естественном языке;

· на специальном (формальном) языке;

· с помощью формул, рисунков, таблиц;

· с помощью стандартных графических объектов (геометрических фигур) – блок-схемы.

Основные элементы блок-схемы.

Название	Символ (рисунок)	Выполняемая функция (пояснение)
1. Блок вычислений		Выполняет вычислительное действие или группу действий
2. Логический блок		Выбор направления выполнения алгоритма в зависимости от условия
3. Блоки ввода/вывода		Ввод или вывод данных вне зависимости от физического носителя
		Вывод данных на печатающее устройство
4. Начало/конец (вход/выход)		Начало или конец программы, вход или выход в подпрограмму
5. Предопределенный процесс		Вычисления по стандартной или пользовательской подпрограмме
6. Блок модификации		Выполнение действий, изменяющих пункты алгоритма
7. Соединитель		Указание связи между прерванными линиями в пределах одной страницы
8. Межстраничный соединитель		Указание связи между частями схемы, расположенной на разных страницах

Виды алгоритмов

Линейный алгоритм - это алгоритм, в котором блоки выполняются по­следовательно сверху вниз от начала до конца.

Линейный алгоритм состоит из последовательности операций, выполняющихся только один раз в порядке следования.

На практике линейные алгоритмы в чистом виде встречаются редко: при расчете арифметических и алгебраических выражений, при расчете по формулам, при решении ряда бытовых задач.

Базовая структура линейного алгоритма:

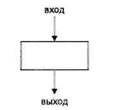 Структура линейного алгоритма